Lernziele
Am Ende dieses Abschnitts werden Sie in der Lage sein:
- Erläutern Sie ein Szenario, in dem sich das magnetische und das elektrische Feld kreuzen und ihre Kräfte sich gegenseitig ausgleichen, während sich ein geladenes Teilchen durch einen Geschwindigkeitsselektor bewegt
- Vergleichen Sie, wie sich Ladungsträger in einem leitenden Material bewegen und erklären Sie, wie dies mit dem Hall-Effekt zusammenhängt
Im Jahr 1879 entwickelte E.H. Hall ein Experiment entwickelt, mit dem man das Vorzeichen der vorherrschenden Ladungsträger in einem leitenden Material bestimmen kann. Aus historischer Sicht war dieses Experiment das erste, das zeigte, dass die Ladungsträger in den meisten Metallen negativ sind.
Besuchen Sie diese Website, um mehr Informationen über den Hall-Effekt zu finden.
Wir untersuchen den Hall-Effekt, indem wir die Bewegung der freien Elektronen entlang eines Metallstreifens der Breite l in einem konstanten Magnetfeld untersuchen (Abbildung \(\PageIndex{1}\)). Die Elektronen bewegen sich von links nach rechts, so dass die magnetische Kraft, die sie erfahren, sie an den unteren Rand des Streifens drückt. Dadurch verbleibt ein Überschuss an positiver Ladung an der oberen Kante des Streifens, was zu einem von oben nach unten gerichteten elektrischen Feld E führt. Die Ladungskonzentration an beiden Kanten baut sich auf, bis die elektrische Kraft auf die Elektronen in einer Richtung durch die magnetische Kraft auf sie in der entgegengesetzten Richtung ausgeglichen ist. Das Gleichgewicht ist erreicht, wenn:
wobei e die Größe der Elektronenladung, \(v_d\) die Driftgeschwindigkeit der Elektronen und E die Größe des durch die getrennte Ladung erzeugten elektrischen Feldes ist. Löst man dies für die Driftgeschwindigkeit, so ergibt sich
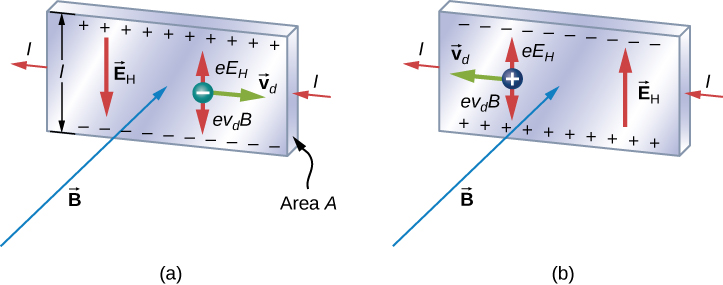
Ein Szenario, bei dem das elektrische und das magnetische Feld senkrecht zueinander stehen, nennt man eine Kreuzfeldsituation. Wenn diese Felder gleiche und entgegengesetzte Kräfte auf ein geladenes Teilchen mit der Geschwindigkeit erzeugen, die den Kräften entspricht, können diese Teilchen eine Apparatur, genannt Geschwindigkeitsselektor, unabgelenkt passieren. Diese Geschwindigkeit ist in Gleichung 11.26} dargestellt. Jede andere Geschwindigkeit eines geladenen Teilchens, das in die gleichen Felder geschickt wird, würde durch die magnetische Kraft oder die elektrische Kraft abgelenkt werden.
Zurück zum Hall-Effekt: Wenn der Strom im Streifen I ist, dann wissen wir aus Strom und Widerstand, dass
wobei n die Anzahl der Ladungsträger pro Volumen und A die Querschnittsfläche des Streifens ist. Die Kombination der Gleichungen für \(v_d\) und I ergibt
Das Feld E ist mit der Potentialdifferenz V zwischen den Kanten des Streifens durch
Die Größe \(V\) wird Hall-Potential genannt und kann mit einem Voltmeter gemessen werden. Die Kombination der Gleichungen für I und E ergibt schließlich
\
wobei die obere Kante des Streifens in Abbildung \(\PageIndex{1}\) gegenüber der unteren Kante positiv ist.
Wir können auch die Gleichung \ref{11.24} und Gleichung \ref{11.28} kombinieren, um einen Ausdruck für die Hall-Spannung in Abhängigkeit vom Magnetfeld zu erhalten:
Was ist, wenn die Ladungsträger positiv sind, wie in Abbildung \(\PageIndex{1}\)? Für den gleichen Strom I ist der Betrag von V immer noch durch Gleichung \ref{hallV} gegeben. Allerdings ist die obere Kante nun negativ in Bezug auf die untere Kante. Daher können wir durch einfache Messung des Vorzeichens von V das Vorzeichen der Hauptladungsträger in einem Metall bestimmen.
Hall-Potentialmessungen zeigen, dass Elektronen die dominierenden Ladungsträger in den meisten Metallen sind. Allerdings zeigen Hall-Potentiale, dass bei einigen wenigen Metallen, wie Wolfram, Beryllium und vielen Halbleitern, die Mehrheit der Ladungsträger positiv ist. Es stellt sich heraus, dass die Leitung durch positive Ladung durch die Wanderung von fehlenden Elektronenplätzen (Löcher genannt) auf Ionen verursacht wird. Die Leitung durch Löcher wird später in der Physik der kondensierten Materie untersucht.
Der Hall-Effekt kann verwendet werden, um Magnetfelder zu messen. Legt man ein Material mit bekannter Ladungsträgerdichte n in ein Magnetfeld und misst V, so kann das Feld aus Gleichung \ref{11.29} bestimmt werden. In Forschungslaboratorien, in denen die Felder von Elektromagneten, die für präzise Messungen verwendet werden, extrem gleichmäßig sein müssen, wird häufig eine „Hallsonde“ als Teil einer elektronischen Schaltung verwendet, die das Feld reguliert.
Beispiel \(\PageIndex{1}\): Geschwindigkeitsselektor
Ein Elektronenstrahl tritt in einen Geschwindigkeitsselektor mit gekreuztem Feld ein, in dem ein magnetisches und ein elektrisches Feld von 2,0 mT bzw. \(6,0 \times 10^3 \, N/C\) herrschen. (a) Wie groß muss die Geschwindigkeit des Elektronenstrahls sein, damit er die gekreuzten Felder unabgelenkt durchläuft? Wenn das elektrische Feld ausgeschaltet wird, (b) wie groß ist die Beschleunigung des Elektronenstrahls und (c) wie groß ist der Radius der daraus resultierenden Kreisbewegung?
Strategie
Der Elektronenstrahl wird weder durch das magnetische noch durch das elektrische Feld abgelenkt, wenn diese Kräfte im Gleichgewicht sind. Aus diesen ausgeglichenen Kräften berechnen wir die Geschwindigkeit des Strahls. Ohne das elektrische Feld wird nur die magnetische Kraft im zweiten Newton’schen Gesetz verwendet, um die Beschleunigung zu finden. Der Radius der Bahn schließlich basiert auf der resultierenden Kreisbewegung aus der magnetischen Kraft.
Lösung
- Die Geschwindigkeit des ungestörten Elektronenstrahls mit gekreuzten Feldern wird durch Gleichung \ref{11.25} berechnet: \
- Die Beschleunigung berechnet sich aus der Nettokraft des Magnetfeldes, gleich Masse mal Beschleunigung. Der Betrag der Beschleunigung ist: \
- Der Radius der Bahn ergibt sich aus dem Gleichgewicht der kreisförmigen und magnetischen Kräfte, oder Gleichung \ref{11.25}: \
Bedeutung
Wenn die Elektronen im Strahl Geschwindigkeiten über oder unter der Antwort in Teil (a) hätten, würden diese Elektronen eine stärkere Nettokraft haben, die entweder vom magnetischen oder elektrischen Feld ausgeübt wird. Daher würden nur die Elektronen mit dieser spezifischen Geschwindigkeit durchkommen.
Das Hall-Potential in einem Silberband
Abbildung \(\PageIndex{2}\) zeigt ein Silberband, dessen Querschnitt 1,0 cm mal 0,20 cm beträgt. Das Band führt von links nach rechts einen Strom von 100 A und liegt in einem gleichmäßigen Magnetfeld der Stärke 1,5 T. Finden Sie unter Verwendung eines Dichtewertes von \(n = 5,9 \times 10^{28}\) Elektronen pro Kubikmeter für Silber das Hall-Potential zwischen den Kanten des Bandes.
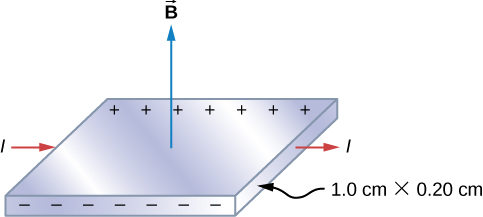
Strategie
Da die Mehrzahl der Ladungsträger Elektronen sind, ist die Polarität der Hall-Spannung die in der Abbildung angegebene. Der Wert der Hall-Spannung wird mit der Gleichung \ref{hallV} berechnet.
Lösung
Bei der Berechnung der Hall-Spannung müssen wir den Strom durch das Material, das Magnetfeld, die Länge, die Anzahl der Ladungsträger und die Fläche kennen. Da dies alles gegeben ist, wird die Hall-Spannung berechnet als:
&= \frac{(100 \, A)(1.5 \, T)(1.0 \times 10^{-2}m)}{(5.9 \times 10^{28} /m^3)(1.6 \times 10^{-19}C)(2.0 \times 10^{-5}m^2)} \\ &= 7,9 \Times 10^{-6}V. \end{align*} \]
Bedeutung
Wie in diesem Beispiel ist das Hall-Potenzial im Allgemeinen sehr klein, und für seine Messung ist ein sorgfältiges Experimentieren mit empfindlichen Geräten erforderlich.
Übung \(\PageIndex{1}\)
Eine Hallsonde besteht aus einem Kupferstreifen, \(n = 8,5 \times 10^{28}\) Elektronen pro Kubikmeter, der 2,0 cm breit und 0,10 cm dick ist. Wie groß ist das Magnetfeld, wenn I = 50 A und das Hall-Potential ist
- \(4,0 \, \mu V\) und
- \(6,0 \, \mu V\)?
Antwort a
1,1 T
Antwort b
1.6 T
Beitragende und Zuschreibungen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen beitragenden Autoren. Dieses Werk ist lizenziert von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0).