Hypothesentest und KonfidenzintervallBearbeiten
Der p-Wert für Kappa wird selten angegeben, wahrscheinlich weil auch relativ niedrige Kappa-Werte zwar signifikant von Null verschieden sein können, aber nicht so groß, dass sie die Untersucher zufriedenstellen.
Konfidenzintervalle für Kappa können für die erwarteten Kappa-Werte bei einer unendlichen Anzahl von geprüften Items mit der folgenden Formel berechnet werden:
C I : κ ± Z 1 – α / 2 S E κ {\displaystyle CI:\kappa \pm Z_{1-\alpha /2}SE_{\kappa }}

Wobei Z 1 – α / 2 = 1,965 {\displaystyle Z_{1-\alpha /2}=1,965}

ist das standardnormale Perzentil, wenn α = 5 % {\displaystyle \alpha =5\%}

, und S E κ = p o ( 1 – p o ) N ( 1 – p e ) 2 {\displaystyle SE_{\kappa }={\sqrt {{p_{o}(1-p_{o})} \over {N(1-p_{e})^{2}}}}}

Dies wird berechnet, indem ignoriert wird, dass pe aus den Daten geschätzt wird, und indem po als eine geschätzte Wahrscheinlichkeit einer Binomialverteilung behandelt wird, während asymptotische Normalität verwendet wird (d. h.: es wird angenommen, dass die Anzahl der Elemente groß ist und dass po weder nahe bei 0 noch bei 1 liegt). S E κ {\displaystyle SE_{\kappa }}

(und der CI im Allgemeinen) kann auch mit Bootstrap-Methoden geschätzt werden.
Interpretieren von magnitudeEdit

Wenn statistische Signifikanz kein nützlicher Leitfaden ist, welche Größe von Kappa spiegelt dann eine angemessene Übereinstimmung wider? Eine Richtlinie wäre hilfreich, aber andere Faktoren als die Übereinstimmung können die Größe beeinflussen, was die Interpretation einer gegebenen Größe problematisch macht. Wie Sim und Wright bemerkten, sind zwei wichtige Faktoren die Prävalenz (sind die Codes äquivalent oder variieren ihre Wahrscheinlichkeiten) und die Verzerrung (sind die Randwahrscheinlichkeiten für die beiden Beobachter ähnlich oder unterschiedlich). Bei sonst gleichen Bedingungen sind die Kappas höher, wenn die Codes equiprobable sind. Andererseits sind die Kappas höher, wenn die Codes für die beiden Beobachter asymmetrisch verteilt sind. Im Gegensatz zu Wahrscheinlichkeitsvariationen ist der Effekt der Verzerrung größer, wenn Kappa klein ist als wenn es groß ist.:261-262
Ein weiterer Faktor ist die Anzahl der Codes. Mit zunehmender Anzahl von Codes wird Kappa höher. Basierend auf einer Simulationsstudie kamen Bakeman und Kollegen zu dem Schluss, dass bei fehlbaren Beobachtern die Werte für kappa niedriger sind, wenn die Anzahl der Codes geringer ist. Und, in Übereinstimmung mit Sim & Wrights Aussage bezüglich der Prävalenz, waren die Kappas höher, wenn die Codes ungefähr gleichwertig waren. Bakeman et al. kamen daher zu dem Schluss, dass „kein einziger Wert von kappa als universell akzeptabel angesehen werden kann“:357 Sie stellen auch ein Computerprogramm zur Verfügung, mit dem Benutzer Werte für kappa berechnen können, indem sie die Anzahl der Codes, ihre Wahrscheinlichkeit und die Genauigkeit des Beobachters angeben. Bei gleichwertigen Codes und Beobachtern, die zu 85 % genau sind, beträgt der Kappa-Wert beispielsweise 0,49, 0,60, 0,66 und 0,69, wenn die Anzahl der Codes 2, 3, 5 bzw. 10 beträgt.
Dessen ungeachtet sind in der Literatur Richtlinien für die Größenordnung erschienen. Die ersten waren vielleicht Landis und Koch, die die Werte < 0 als keine Übereinstimmung und 0-0,20 als gering, 0,21-0,40 als mittelmäßig, 0,41-0,60 als erheblich und 0,81-1 als fast perfekte Übereinstimmung charakterisierten. Diese Richtlinien werden jedoch keineswegs allgemein akzeptiert; Landis und Koch lieferten keine Beweise, um sie zu unterstützen, sondern stützten sich stattdessen auf persönliche Meinungen. Es wurde angemerkt, dass diese Richtlinien eher schädlich als hilfreich sein können. Fleiss’s:218 ebenso willkürliche Richtlinien charakterisieren Kappas über 0,75 als exzellent, 0,40 bis 0,75 als fair bis gut und unter 0,40 als schlecht.
Kappa maximumEdit
Kappa nimmt seinen theoretischen Maximalwert von 1 nur dann an, wenn beide Beobachter die Codes gleich verteilen, d.h. wenn die entsprechenden Zeilen- und Spaltensummen identisch sind. Alles, was darunter liegt, ist weniger als perfekte Übereinstimmung. Dennoch hilft der maximale Wert, den kappa bei ungleichen Verteilungen erreichen könnte, bei der Interpretation des tatsächlich erreichten kappa-Wertes. Die Gleichung für κ max lautet:
κ max = P max – P exp 1 – P exp {\displaystyle \kappa _{\max }={\frac {P_{\max }-P_{\exp }}{1-P_{\exp }}}}

wobei P exp = ∑ i = 1 k P i + P + i {\displaystyle P_{\exp }=\sum _{i=1}^{k}P_{i+}P_{+i}}

, wie üblich, P max = ∑ i = 1 k min ( P i + , P + i ) {\displaystyle P_{\max }=\sum _{i=1}^{k}\min(P_{i+},P_{+i})}

,
k = Anzahl der Codes, P i + {\displaystyle P_{i+}}

sind die Zeilenwahrscheinlichkeiten, und P + i {\displaystyle P_{+i}}

sind die Spaltenwahrscheinlichkeiten.
Einschränkungen
Kappa ist ein Index, der die beobachtete Übereinstimmung in Bezug auf eine Basisübereinstimmung berücksichtigt. Forscher müssen jedoch sorgfältig abwägen, ob die Basislinienübereinstimmung von Kappa für die jeweilige Forschungsfrage relevant ist. Die Kappa-Basisübereinstimmung wird häufig als die Übereinstimmung aufgrund des Zufalls beschrieben, was nur teilweise richtig ist. Die Kappa-Basisübereinstimmung ist die Übereinstimmung, die aufgrund einer zufälligen Zuordnung zu erwarten wäre, wenn die durch die Randsummen der quadratischen Kontingenztabelle spezifizierten Größen gegeben wären. Somit ist Kappa = 0, wenn die beobachtete Zuordnung offensichtlich zufällig ist, unabhängig von der durch die Randsummen eingeschränkten Mengenübereinstimmung. Bei vielen Anwendungen sollten die Untersucher jedoch mehr an der Mengenabweichung in den Randsummen interessiert sein als an der Zuordnungsabweichung, die durch die zusätzlichen Informationen auf der Diagonale der quadratischen Kontingenztabelle beschrieben wird. Daher ist die Kappa-Basislinie für viele Anwendungen eher ablenkend als aufklärend. Betrachten Sie das folgende Beispiel:
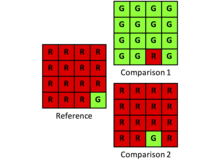
Kappa-Beispiel
| Referenz | |||
|---|---|---|---|
| G | R | ||
| Vergleich | G | 1 | 14 |
| R | 0 | 1 | |
Der Anteil der Unstimmigkeiten beträgt 14/16 oder 0.875. Die Unstimmigkeit ist auf die Menge zurückzuführen, da die Zuordnung optimal ist. Kappa ist 0,01.
| Referenz | |||
|---|---|---|---|
| G | R | ||
| Vergleich | G | 0 | 1 |
| R | 1 | 14 | |
Der Unstimmigkeitsanteil beträgt 2/16 oder 0.125. Die Unstimmigkeit ist auf die Zuordnung zurückzuführen, da die Mengen identisch sind. Kappa ist -0,07.
Hier ist die Angabe von Mengen- und Zuordnungsdiskrepanzen informativ, während Kappa Informationen verschleiert. Außerdem bringt Kappa einige Herausforderungen bei der Berechnung und Interpretation mit sich, da Kappa eine Kennzahl ist. Es ist möglich, dass die Kappa-Kennzahl aufgrund von Null im Nenner einen undefinierten Wert liefert. Darüber hinaus offenbart ein Verhältnis weder seinen Zähler noch seinen Nenner. Es ist informativer, wenn die Forscher die Unstimmigkeit in zwei Komponenten, der Quantität und der Zuordnung, angeben. Diese beiden Komponenten beschreiben die Beziehung zwischen den Kategorien deutlicher als eine einzelne zusammenfassende Statistik. Wenn die Vorhersagegenauigkeit das Ziel ist, können Forscher leichter über Möglichkeiten zur Verbesserung einer Vorhersage nachdenken, indem sie zwei Komponenten der Menge und der Zuordnung verwenden, anstatt nur ein Kappa-Verhältnis.
Einige Forscher haben Bedenken über die Tendenz von κ geäußert, die Häufigkeiten der beobachteten Kategorien als gegeben anzunehmen, was es für die Messung der Übereinstimmung in Situationen wie der Diagnose seltener Krankheiten unzuverlässig machen kann. In diesen Situationen neigt κ dazu, die Übereinstimmung bei der seltenen Kategorie zu unterschätzen. Aus diesem Grund wird κ als ein zu konservatives Maß für die Übereinstimmung angesehen. Andere bestreiten die Behauptung, dass kappa die zufällige Übereinstimmung „berücksichtigt“. Um dies effektiv zu tun, wäre ein explizites Modell erforderlich, wie der Zufall die Entscheidungen der Bewerter beeinflusst. Die sogenannte Zufallsanpassung der Kappa-Statistik geht davon aus, dass die Bewerter, wenn sie sich nicht ganz sicher sind, einfach raten – ein sehr unrealistisches Szenario.