Einführung
Die Regressionsanalyse wird üblicherweise zur Modellierung der Beziehung zwischen einer einzelnen abhängigen Variable Y und einem oder mehreren Prädiktoren verwendet. Wenn wir einen Prädiktor haben, nennen wir dies „einfache“ lineare Regression:
E = β0 + β1X
Das heißt, der Erwartungswert von Y ist eine geradlinige Funktion von X. Die Betas werden ausgewählt, indem die Linie gewählt wird, die den quadratischen Abstand zwischen jedem Y-Wert und der Linie der besten Anpassung minimiert. Die Betas werden so gewählt, dass sie diesen Ausdruck minimieren:
∑i (yi – (β0 + β1X))2
Eine instruktive Grafik habe ich im Internet gefunden

Quelle: http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Wenn wir mehr als einen Prädiktor haben, sprechen wir von multipler linearer Regression:
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
Die angepassten Werte (d.h., die vorhergesagten Werte) sind definiert als die Werte von Y, die erzeugt werden, wenn wir unsere X-Werte in unser angepasstes Modell stecken.
Die Residuen sind die angepassten Werte minus die tatsächlich beobachteten Werte von Y.
Hier ist ein Beispiel für eine lineare Regression mit zwei Prädiktoren und einem Ergebnis:
Anstelle der „line of best fit“ gibt es eine „plane of best fit“
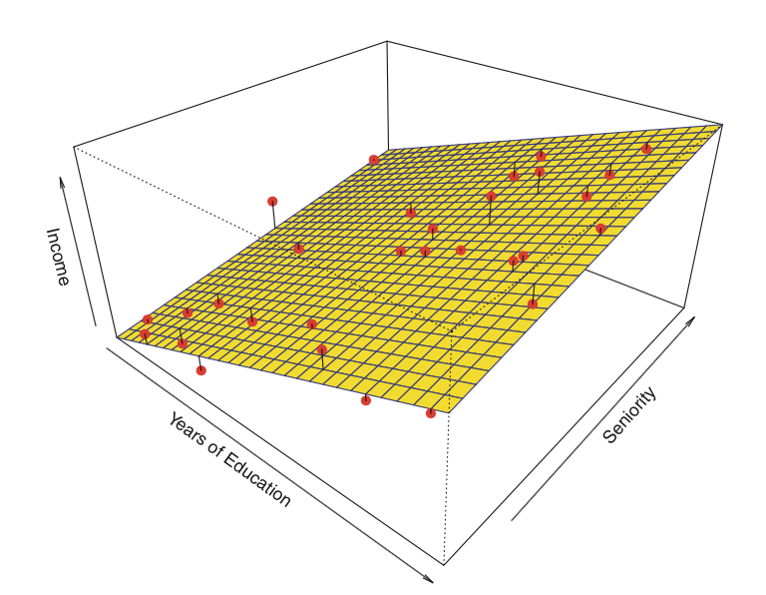
Quelle: James et al. Introduction to Statistical Learning (Springer 2013)
Es gibt vier Annahmen, die mit einem linearen Regressionsmodell verbunden sind:
- Linearität: Der Zusammenhang zwischen X und dem Mittelwert von Y ist linear.
- Homoskedastizität: Die Varianz der Residuen ist für jeden Wert von X gleich.
- Unabhängigkeit: Die Beobachtungen sind unabhängig voneinander.
- Normalität: Für jeden festen Wert von X ist Y normalverteilt.
Wir werden später im Modul überprüfen, wie diese Annahmen zu bewerten sind.
Lassen Sie uns mit einer einfachen Regression beginnen. In R werden Modelle typischerweise durch den Aufruf einer Modellanpassungsfunktion, in unserem Fall lm(), mit einem „formula“-Objekt, das das Modell beschreibt, und einem „data.frame“-Objekt, das die in der Formel verwendeten Variablen enthält, angepasst. Ein typischer Aufruf könnte so aussehen
> myfunction <- lm(formula, data, …)
und es wird ein gefittetes Modellobjekt zurückgegeben, hier als myfunction gespeichert. Dieses angepasste Modell kann dann anschließend gedruckt, zusammengefasst oder visualisiert werden; außerdem können die angepassten Werte und Residuen extrahiert werden, und wir können Vorhersagen für neue Daten (Werte von X) machen, die mit Funktionen wie summary(), residuals(),predict() usw. berechnet werden. Als Nächstes schauen wir uns an, wie man eine einfache lineare Regression anpasst.
Zum Anfang zurückkehren | vorherige Seite | nächste Seite