Falsch Positive und Falsch Negative: Definition und Beispiele

Statistik-Definitionen> Falsch positiv und falsch negativ

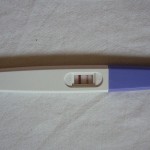
Bild:Nabokov|Wikimedia Commons

Was ist ein falsches Positiv?

Ein falsches Positiv ist, wenn Sie ein positives Ergebnis für einen Test erhalten, obwohl Sie ein negatives Ergebnis hätten erhalten sollen. Es wird manchmal als „falscher Alarm“ oder „falsch positiver Fehler“ bezeichnet. Es wird normalerweise im medizinischen Bereich verwendet, kann aber auch auf andere Bereiche (wie Softwaretests) zutreffen. Einige Beispiele für falsch positive Ergebnisse:

• Ein Schwangerschaftstest ist positiv, obwohl Sie nicht schwanger sind.
• Ein Krebs-Früherkennungstest ist positiv, aber Sie haben die Krankheit nicht.
• Ein pränataler Test ist positiv für das Down-Syndrom, obwohl Ihr Fötus die Störung nicht hat(1).
• Virensoftware auf Ihrem Computer identifiziert ein harmloses Programm fälschlicherweise als bösartig.

Falsch-positive Ergebnisse können beunruhigend sein, besonders wenn es um medizinische Tests geht. Forscher versuchen ständig, Gründe für falsch positive Ergebnisse zu finden, um Tests empfindlicher zu machen.

Ein verwandtes Konzept ist ein falsch negatives Ergebnis, bei dem Sie ein negatives Ergebnis erhalten, obwohl Sie ein positives hätten erhalten sollen. Zum Beispiel kann ein Schwangerschaftstest ein negatives Ergebnis liefern, obwohl Sie tatsächlich schwanger sind.

Das Falsch-Positiv-Paradox

Wenn ein Test für eine Krankheit zu 99% genau ist und Sie ein positives Ergebnis erhalten, wie hoch ist dann die Wahrscheinlichkeit, dass Sie die Krankheit tatsächlich haben?

Wenn Sie 99% sagen, werden Sie vielleicht überrascht sein, dass Sie falsch liegen. Wenn die Krankheit sehr häufig vorkommt, könnte Ihre Chance bei 99 % liegen. Aber je seltener die Krankheit ist, desto ungenauer ist der Test und desto geringer ist die Wahrscheinlichkeit, dass Sie die Krankheit tatsächlich haben. Der Unterschied kann ziemlich dramatisch sein. Wenn Sie z. B. positiv auf eine seltene Krankheit getestet werden (eine, die z. B. 1 von 1.000 Menschen betrifft), kann Ihre Wahrscheinlichkeit, die Krankheit tatsächlich zu haben, weniger als ein Prozent betragen! Der Grund dafür ist die bedingte Wahrscheinlichkeit.

Falsch-Positive und Typ-I-Fehler

In der Statistik wird ein falsches Positiv normalerweise als Typ-I-Fehler bezeichnet. Ein Fehler vom Typ I liegt vor, wenn Sie die Nullhypothese fälschlicherweise ablehnen. Dies erzeugt ein „falsches Positiv“ für Ihre Forschung, was Sie zu der Annahme verleitet, dass Ihre Hypothese (d.h. die Alternativhypothese) wahr ist, obwohl sie es in Wirklichkeit nicht ist.

Das Drogentest-Paradoxon und HIV-Tests

Das bloße ANSEHEN eines solchen Bildes macht mich nervös!

Sie machen einen HIV-Test, der zu 99% genau ist und der Test ist positiv. Wie hoch ist die Wahrscheinlichkeit, dass Sie HIV-positiv sind?

1. Richtig hoch: 99%. Ich flippe aus.
2. Richtig niedrig. Wahrscheinlich etwa 1 zu 100. Ich werde darüber schlafen und dann den Test noch einmal machen.

Wenn Sie 1(99%) geantwortet haben, liegen Sie falsch. Aber keine Sorge – Sie sind nicht allein. Die meisten Leute werden auf die gleiche Weise antworten wie Sie. Aber Tatsache ist (vorausgesetzt, Sie gehören zu einer niedrigen Risikogruppe), dass Sie nur eine sehr geringe Chance haben, das Virus tatsächlich zu haben, selbst wenn Sie positiv auf den HIV-Test getestet werden. Das nennt man das Drogentest-Paradoxon.

Wie?

Ein HIV-Test (oder jeder andere Test auf Krankheiten) ist nicht zu 99% genau für Sie, sondern zu 99% genau für eine Population.* Nehmen wir an, es gibt 100.000 Menschen in einer Population und eine Person hat das HIV-Virus. Diese eine Person mit HIV wird wahrscheinlich positiv auf das Virus getestet (mit der 99%igen Genauigkeit des Tests). Aber was ist mit den anderen 99.999? Der Test wird sich in 1% der Fälle irren, was bedeutet, dass von 99.999 Personen, die kein HIV haben, etwa 100 positiv getestet werden.

Mit anderen Worten: Wenn 100.000 Menschen den Test machen, werden 101 positiv getestet, aber nur einer hat tatsächlich das Virus.

Sorgen Sie sich nicht, wenn dieses Paradoxon ein wenig verwirrend ist. Sogar Ärzte machen es falsch. Es gibt mehrere Studien, die zeigen, dass Ärzte Patienten oft alarmieren, indem sie ihnen mitteilen, dass sie ein viel höheres Risiko für eine bestimmte Krankheit haben, als die Statistik tatsächlich angibt (siehe diesen Artikel in U.S. News).

Peter Donnely ist ein englischer Statistiker, der die obigen Informationen in einem wirklich faszinierenden TED Talk darüber, wie Menschen von Statistiken getäuscht werden, aufgenommen hat. Wenn Sie ihn noch nicht gesehen haben, ist er einen Blick wert, vor allem, weil er das Problem hervorhebt, dass Juristen Statistiken falsch verstehen:

*Diese Zahlen sind nicht ganz genau – die tatsächliche Prävalenz von HIV in einer Bevölkerung hängt von Ihrem Lebensstil und anderen Risikofaktoren ab. Ende 2008 gab es in den USA etwa 1,2 Millionen Menschen mit HIV, bei einer Gesamtbevölkerung von 304.059.724. Außerdem sind die meisten HIV-Tests heute zu 99,9 % genau.

Was ist ein falsches Negativ?

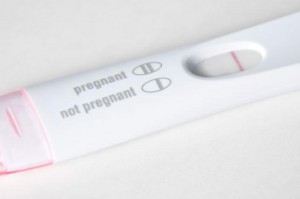
Nur weil ein Test sagt, er sei negativ, heißt das nicht, dass er zu 100 % genau ist. Bild: University of Iowa

Ein falsches Negativ liegt vor, wenn ein negatives Testergebnis falsch ist. Mit anderen Worten: Sie erhalten ein negatives Testergebnis, hätten aber ein positives Testergebnis erhalten sollen. Zum Beispiel könnten Sie einen Schwangerschaftstest machen und er kommt als negativ zurück (nicht schwanger). Tatsächlich sind Sie aber schwanger. Ein falsches negatives Ergebnis bei einem Schwangerschaftstest könnte darauf zurückzuführen sein, dass Sie den Test zu früh machen, verdünnten Urin verwenden oder das Ergebnis zu früh überprüfen. Bei so gut wie jedem medizinischen Test besteht das Risiko eines falsch negativen Ergebnisses. Zum Beispiel kann ein Krebstest ein negatives Ergebnis liefern, obwohl Sie in Wirklichkeit die Krankheit haben. Falsch-negative Ergebnisse können auch in anderen Bereichen auftreten, wie z.B.:

• Qualitätskontrolle in der Produktion; ein falsch-negatives Ergebnis in diesem Bereich bedeutet, dass ein fehlerhafter Artikel durch die Maschen fällt.
• Bei Softwaretests würde ein falsches Negativ bedeuten, dass ein Test, der etwas auffangen soll (z. B. einen Virus), fehlgeschlagen ist.
• Im Justizsystem tritt ein falsches Negativ auf, wenn ein schuldiger Verdächtiger für „nicht schuldig“ befunden wird und frei herumlaufen darf.

Falsche Negative schaffen zwei Probleme. Das erste ist ein falsches Gefühl der Sicherheit. Wenn z. B. Ihre Fertigungslinie keine fehlerhaften Artikel abfängt, denken Sie vielleicht, dass der Prozess effektiver läuft, als er tatsächlich ist. Das zweite, potenziell schwerwiegendere Problem ist, dass potenziell gefährliche Situationen übersehen werden können. Zum Beispiel kann ein lähmender Computervirus verheerende Folgen haben, wenn er nicht erkannt wird, oder eine krebskranke Person wird möglicherweise nicht rechtzeitig behandelt.

Falsch-negative Ergebnisse bei Hypothesentests

Falsch-negative Ergebnisse können bei der Durchführung eines Hypothesentests auftreten. Wenn Sie fälschlicherweise ein negatives Ergebnis erhalten und die Nullhypothese nicht verwerfen (obwohl Sie es sollten), wird dies als Fehler vom Typ II bezeichnet.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, S. 536 und 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Unternehmen

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf diesem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!