Introduction
Alpha-Diversity-Metriken fassen die Struktur einer ökologischen Gemeinschaft in Bezug auf ihren Reichtum (Anzahl der taxonomischen Gruppen), ihre Gleichmäßigkeit (Verteilung der Häufigkeiten der Gruppen) oder beides zusammen. Da sich viele Störungen einer Gemeinschaft auf die Alpha-Diversität einer Gemeinschaft auswirken, ist die Zusammenfassung und der Vergleich der Gemeinschaftsstruktur über die Alpha-Diversität ein allgegenwärtiger Ansatz zur Analyse von Gemeinschaftserhebungen. In der mikrobiellen Ökologie ist die Analyse der Alpha-Diversität von Amplikon-Sequenzierungsdaten ein gängiger erster Ansatz zur Bewertung von Unterschieden zwischen Umgebungen.
Leider ist es nicht trivial zu bestimmen, wie man die Alpha-Diversität sinnvoll schätzen und vergleichen kann. Betrachten Sie zur Veranschaulichung das folgende Beispiel, bei dem die interessierende Alpha-Diversity-Metrik der Stamm-Reichtum einer mikrobiellen Gemeinschaft ist (die Gesamtzahl der in der Umgebung vorhandenen Stammvarianten). Angenommen, ich führe ein Experiment durch, bei dem ich eine Probe aus Umgebung A entnehme und die Anzahl der verschiedenen mikrobiellen Taxa in meiner Probe zähle. Dann nehme ich eine Probe aus Umgebung B, zähle die Anzahl der verschiedenen Taxa in dieser Probe und vergleiche sie mit der Anzahl der Taxa in Umgebung A. Ich werde wahrscheinlich eine höhere Anzahl verschiedener Taxa in der Probe mit mehr mikrobiellen Reads beobachten. Die Bibliotheksgrößen können die Biologie bei der Bestimmung des Ergebnisses der Diversitätsanalyse dominieren (Lande, 1996).
Rarefaction ist eine Methode, die die Unterschiede in den Bibliotheksgrößen zwischen den Proben ausgleicht, um Vergleiche der Alpha-Diversität zu erleichtern. Erstmals von Sanders (1968) vorgeschlagen, beinhaltet Rarefaction die Auswahl einer bestimmten Anzahl von Proben, die gleich oder kleiner als die Anzahl der Proben in der kleinsten Probe ist, und dann das zufällige Verwerfen von Reads aus größeren Proben, bis die Anzahl der verbleibenden Proben gleich diesem Schwellenwert ist (siehe Hurlbert, 1971 für eine deterministische Version). Basierend auf diesen Teilproben gleicher Größe können Diversitätsmetriken berechnet werden, die Ökosysteme „fair“ kontrastieren können, unabhängig von Unterschieden in den Probengrößen (Weiss et al., 2017).
Leider ist die Rarefaction weder gerechtfertigt noch notwendig, eine Ansicht, die von McMurdie und Holmes (2014) im Kontext des Vergleichs relativer Abundanzen statistisch gerahmt wird. In diesem Artikel diskutiere ich, warum ungleiche Stichprobengrößen besondere Probleme bei der Analyse der Alpha-Diversität zu verursachen scheinen. Ich führe eine statistische Perspektive auf die Schätzung der Alpha-Diversität ein und argumentiere, dass eine gängige Sichtweise von Diversitätsindizes grundlegende Probleme beim Vergleich von Proben verursacht. Ohne ein bestimmtes Modell der mikrobiellen Probenahme zu befürworten, schlage ich einen allgemeinen Ansatz zum Vergleich der mikrobiellen Diversität vor, der die Unsicherheit bei der Schätzung von Diversitätsmetriken berücksichtigt. Da jedoch Schätzungen für Alpha-Diversitätsmetriken stark verzerrt sind, wenn Taxa unbeobachtet sind, sollte ein Vergleich der Alpha-Diversität unter Verwendung von Roh- oder Rarefied-Daten nicht vorgenommen werden. Ich beschreibe eine statistische Methodik für die Alpha-Diversitätsanalyse, die fehlende Taxa bereinigt und die anstelle der bestehenden üblichen Ansätze zur Diversitätsanalyse in der Ökologie verwendet werden sollte. Während der Schwerpunkt der Beispiele auf der Analyse von Mikrobiomdaten liegt, sind die Probleme und die Diskussion gleichermaßen auf die Analyse makroökologischer Daten anwendbar. Darüber hinaus gilt diese Diskussion auch für Diversitätsanalysen, die auf Stamm-, Art- oder anderer taxonomischer Ebene durchgeführt werden.
Messfehler und Varianz in Mikrobiom-Studien
Stellen Sie sich vor, wir hätten vollständiges Wissen über jede existierende Mikrobe, einschließlich Identität, Abundanz und Standort. Um die mikrobielle Diversität zu vergleichen, würden wir spezifische Umgebungen definieren (z. B. den distalen Darm von Frauen im Alter von 35 Jahren, die in den zusammenhängenden USA leben) und Diversitätsmetriken über verschiedene ökologische Gradienten hinweg vergleichen (z. B. mit oder ohne Reizdarmsyndrom-Diagnose). Die Alpha-Diversität könnte genau verglichen werden, weil wir ganze mikrobielle Populationen mit perfekter Präzision kennen würden.
Leider haben wir nicht das Wissen über jede Mikrobe. Wir nehmen Proben aus der Umgebung und untersuchen die in der Probe vorhandene mikrobielle Gemeinschaft. Wir nutzen unsere Erkenntnisse über die Probe, um Rückschlüsse auf die Umgebung zu ziehen, die uns wirklich interessiert. Die Proben sind nicht von besonderem Interesse, außer dass sie die Umgebung widerspiegeln, aus der sie entnommen wurden. Je mehr Proben wir aus der Umgebung entnehmen und je größer die Proben sind, desto näher kommen wir dem Verständnis der wahren und gesamten mikrobiellen Gemeinschaft, die uns interessiert. Das bedeutet, dass sich unsere Berechnung einer beliebigen Diversitätsmetrik mit zunehmender Beprobung dem Wert dieser Diversitätsmetrik annähert, der unter Verwendung der gesamten Population berechnet wurde.
Die Beobachtung kleiner Proben aus einer großen Population ist kein Versuchsaufbau, der nur in der mikrobiellen Ökologie vorkommt: Er ist in der Statistik fast universell. Der Aufbau, bei dem eine Schätzung einer Größe zum richtigen Wert konvergiert, wenn mehr Stichproben erhalten werden, ist in der Statistik ebenfalls gut bekannt. Die einzigartige Eigenschaft von Mikrobiomexperimenten und Alpha-Diversitätsanalysen ist, dass die Proben nicht die gesamte untersuchte mikrobielle Gemeinschaft repräsentieren. Es gibt einen unangepassten Fehler, wenn wir unsere Proben als Stellvertreter für die gesamte Gemeinschaft verwenden.
Um diesen Unterschied zu veranschaulichen, stelle ich mikrobielle Diversitätsexperimente einem nicht-mikrobiellen Experiment gegenüber. Nehmen wir an, wir sind an der Modellierung des CO2-Flusses von Böden interessiert, die mit verschiedenen Zusatzstoffen behandelt wurden. Wir würden den Fluss von gleich großen Bodenstellen messen, die mit den verschiedenen Zusatzstoffen behandelt wurden, und biologische Replikate mit mehreren Stellen für jeden Zusatzstoff durchführen. Um zu beurteilen, ob die Zusatzstoffe den Fluss beeinflussen, würden wir ein Regressionsmodell (z. B. ANOVA) auf den Fluss mit den Zusatzstoffen als erklärende Variable anwenden. Implizit erkennt dieses Modell an, dass wir den Fluss mit hoher Präzision bewerten können, d.h. die Fehlermarge für die Bestimmung des Flusses ist vernachlässigbar.
Angenommen, wir wüssten, dass unsere Flussmessmaschine den Fluss durchweg um genau 5 Einheiten unterschätzt. Wir würden den Messfehler ausgleichen, indem wir 5 Einheiten zu jeder Messung addieren, bevor wir sie vergleichen. Aber was passiert, wenn wir einen zufälligen Messfehler haben? Wenn der Messfehler der Maschine zufällig wäre (z. B. mit einem Mittelwert von 0 und einer Varianz von 1 Einheit für alle Änderungen), würde sich dies nicht auf eine bestimmte Änderung auswirken. Allerdings wäre es statistisch schwieriger, einen Unterschied zwischen den Auswirkungen der Änderungen auf den Fluss zu erkennen: Wir würden mehr Stichproben benötigen, um einen echten Unterschied zu erkennen, als im Fall ohne Messfehler. Um das zusätzliche experimentelle Rauschen zu berücksichtigen, würden wir ein Modell verwenden, das den Messfehler bei der Bewertung der Unterschiede zwischen den Änderungen berücksichtigt. Wenn die Varianz des Messfehlers 1 Einheit für Änderung A, aber 5 Einheiten für Änderung B beträgt, würden wir ebenfalls mit einem Messfehlermodell korrigieren.
Um zu entscheiden, ob Messfehler bei Beobachtungen in einem Experiment berücksichtigt werden müssen, ist es notwendig, die Auswirkung der Wiederholung des Beobachtungsprozesses an derselben Versuchseinheit zu berücksichtigen. Im Flux-Experiment würde dies bedeuten, dass der Flux an denselben Bodenstellen unter denselben Versuchsbedingungen erneut gemessen wird. Ohne Messfehler in den Beobachtungen würden wir durchgängig die gleiche Flussmessung beobachten, während wir bei zufälligen Messfehlern höchstwahrscheinlich leicht unterschiedliche Flussmessungen beobachten würden. Da technische Replikate in Mikrobiomexperimenten unterschiedliche Anzahlen von Reads, unterschiedliche Gemeinschaftszusammensetzungen und unterschiedliche Niveaus der Alpha-Diversität ergeben, haben wir Messfehler in mikrobiellen Experimenten.
Voreingenommenheit bei der Schätzung und dem Vergleich der Alpha-Diversität
Während Messfehler in Mikrobiom-Studien alle Analysen von Mikrobiom-Daten betreffen, ist die Alpha-Diversität besonders betroffen, da die üblicherweise verwendeten Schätzungen der Alpha-Diversität im Vergleich zu anderen Schätzungsproblemen in der mikrobiellen Ökologie (z. B. Schätzung der relativen Häufigkeiten) stark verzerrt sind. In der statistischen Literatur gibt es einige Werkzeuge, um Probleme mit der Verzerrung der Alpha-Diversität anzugehen (Chao und Bunge, 2002; Willis und Bunge, 2015; Arbel et al., 2016; Willis und Martin, 2018). Es gibt jedoch zwei falsche Praktiken rund um die Alpha-Diversität, die die Verbreitung von statistisch motivierten Methoden verhindern. Die erste Praxis ist die Verwendung verzerrter Schätzungen von Alpha-Diversitätsindizes. Die zweite Praxis ist die Behandlung von Alpha-Diversitäts-Schätzungen als präzise beobachtete Größen, die keinen Messfehler aufweisen.
Um diese Diskussion zu verdeutlichen, werde ich mich auf die taxonomische Reichhaltigkeit (den einfachsten Fall) konzentrieren und das Argument später auf andere Alpha-Diversitätsmetriken verallgemeinern. Betrachten wir die Situation in Abbildung 1A, in der wir zwei verschiedene Umgebungen untersuchen, und die Reichhaltigkeit von Umgebung A (nennen wir sie CA) ist höher als die Reichhaltigkeit von Umgebung B (CB). Angenommen, wir haben zwei biologische Replikate von Proben aus jeder Umgebung: nA1 und nA2 Reads aus Umgebung A, nB1 und nB2 Reads aus Umgebung B, und nA1 < nB1 < nA2 < nB2. Sei cij der beobachtete Reichtum der Umgebung i auf dem Replikat j. Wie in der Praxis üblich, kann cA1 < cA2 < cB1 < cB2 sein.
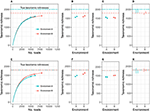
Abbildung 1. Der erwartete taxonomische Reichtum der Probe steigt mit der Anzahl der Reads (A,E). Der Vergleich des taxonomischen Reichtums von Proben kann daher oft zu falschen Schlussfolgerungen über den wahren Reichtum führen (B,F). Das Seltenmachen von Proben auf dieselbe Anzahl von Reads kann ebenfalls zu falschen Schlussfolgerungen führen (C,G). Die Anpassung für nicht beobachtete Taxa und die Berücksichtigung der Unsicherheit in der Schätzung erkennt sowohl wahre (D) als auch falsche (H) Unterschiede in der Reichhaltigkeit korrekt. Während das hier verwendete Beispiel die mikrobielle Reichhaltigkeit betrifft, gilt das gleiche Argument für die makroökologische Reichhaltigkeit sowie für andere Alpha-Diversitätsindizes.
Es gibt derzeit zwei häufig verwendete Methoden zum Vergleich der Alpha-Diversität. Die erste Methode, Abbildung 1B, besteht darin, die Schätzungen cA1, cA2, cB1 und cB2 zu verwenden und die Modellierung und Hypothesentests (z. B. ANOVA) so durchzuführen, als ob sowohl der Bias als auch die Varianz dieser Schätzungen null wären (siehe z. B. Makipaa et al., 2017). In der Umgebung von Abbildung 1A führt dies zu der fälschlichen Schlussfolgerung, dass Umgebung A eine geringere Reichhaltigkeit als Umgebung B aufweist. Die zweite Methode besteht darin, eine normalisierte oder rarefied Stichprobe zu erzeugen, indem zufällig Reads aus allen Stichproben verworfen werden, bis jede Stichprobe nA1 Reads (die Anzahl der Reads in der kleinsten Stichprobe) aufweist (Abbildung 1C). Die resultierenden Rarefied Richness Levels sind dann cA1, cA2′, cB1′ und cB2′. Diese Schätzungen werden dann für die Modellierung und Hypothesentests verwendet (siehe z. B. Arora et al., 2017). Dies führt zu der Schlussfolgerung, dass Umwelt A und Umwelt B keinen signifikant unterschiedlichen Reichtum aufweisen und die Schätzungen des Reichtums weit unter dem tatsächlichen Reichtum der einzelnen Ökosysteme liegen (es gibt eine erhebliche negative Verzerrung in den Schätzungen), was einen Vergleich des Reichtums zwischen verschiedenen Experimenten unmöglich macht. Außerdem wurden nicht alle Informationen, die aus den Proben gesammelt wurden, für den Vergleich verwendet.
Hier plädiere ich für eine dritte Strategie: Passen Sie die Stichproben-Reichheit jedes Ökosystems an, indem Sie eine Schätzung der Anzahl der unbeobachteten Arten hinzufügen, schätzen Sie die Varianz in der Gesamt-Reichheitsschätzung und vergleichen Sie die Diversitäten relativ zu diesen Fehlern (Abbildung 1D). Diese Option hat den Vorteil, dass sie alle beobachteten Reads nutzt, die Schätzungen des tatsächlich interessierenden Parameters (taxonomischer Reichtum) vergleicht und das experimentelle Rauschen berücksichtigt. In dem Fall, in dem die Umgebungen den gleichen Reichtum aufweisen (Abbildungen 1E-H), erkennt dieser Ansatz korrekt den gleichen Reichtum, auch wenn sich die Abundanzstrukturen unterscheiden.
Die Modellierung von Parametern, die mit Schätzfehlern beobachtet wurden, ist kein neuer Vorschlag: Dieser Ansatz stammt aus dem Bereich der statistischen Meta-Analyse, in der die Ergebnisse mehrerer Studien, die die gleiche Effektgröße schätzen, verglichen werden (Demidenko, 2004; Willis et al., 2016; Washburne et al., 2018). In Meta-Analysen müssen größere Studien bei der Bestimmung der Gesamteffektgröße stärker gewichtet werden, und dies wird in einer Meta-Analyse über die kleineren Standardfehler der Effektgrößenschätzungen berücksichtigt. In ähnlicher Weise wird beim Vergleich des Ansprechens verschiedener Behandlungsgruppen in klinischen Studien die Anzahl der Probanden in jeder Behandlungsgruppe bei einem Vergleich des Gesamteffekts der Behandlung berücksichtigt. Die Anpassung an die Stichprobengröße beim Vergleich verschiedener Gruppen von Beobachtungen, ohne Daten zu verwerfen, ist in den Wissenschaften weit verbreitet, und das Verwerfen von Daten zur Anpassung an ungleiche Stichprobengrößen ist die Ausnahme. Die hier skizzierte Strategie zur Modellierung der Reichhaltigkeit nach der Bereinigung um fehlende Arten berücksichtigt sowohl Verzerrungen als auch Varianz und trägt damit Unterschieden in der Bibliotheksgröße und unvollständigen mikrobiellen Erhebungen Rechnung.
Während das hier diskutierte Beispiel die Reichhaltigkeit ist, könnte dieser Ansatz zur Schätzung und zum Vergleich der Alpha-Diversität unter Verwendung einer Verzerrungskorrektur (Einbeziehung unbeobachteter Taxa) und einer Varianzanpassung (Messfehlermodell) auf jede Alpha-Diversitätsmetrik angewendet werden. Für die Reichtumsschätzung gibt es jedoch eine gut untersuchte statistische Literatur, und es existieren Reichtumsschätzer, die an Mikrobiomdaten angepasst sind (siehe Bunge et al., 2014 für eine Übersicht). Das Gleiche gilt nicht für andere Alpha-Diversitätsmetriken. Zum Beispiel liefern die Chao-Bunge- (Chao und Bunge, 2002) und Breakaway- (Willis und Bunge, 2015) Schätzer für taxonomische Reichhaltigkeit Varianzschätzungen, berücksichtigen unbeobachtete Taxa und sind nicht übermäßig empfindlich gegenüber der Singleton-Anzahl (die Anzahl der einmal beobachteten Arten). Im Gegensatz dazu liefert der abdeckungsbereinigte Entropieschätzer des Shannon-Index (Chao und Shen, 2003) Varianzschätzungen und berücksichtigt unbeobachtete Taxa, ist aber extrem empfindlich gegenüber der Singleton-Anzahl, die in Mikrobiom-Studien oft schwer zu bestimmen ist. Während die Schätzung der Alpha-Diversität für Mikrobiome ein aktives Forschungsgebiet in der Statistik ist (Arbel et al., 2016; Zhang und Grabchak, 2016; Willis und Martin, 2018), gibt es nach wie vor viele Merkmale mikrobieller Ökosysteme (wie z. B. Crosstalk zwischen Proben und räumliche Organisation von Mikroben), die noch nicht in die statistische Methodik zur Schätzung der Alpha-Diversität einbezogen sind. Trotzdem sind Alpha-Diversitäts-Schätzungen, die unbeobachtete Taxa berücksichtigen und Varianzschätzungen liefern, sowohl Plug-in-Schätzungen als auch Rarefied-Schätzungen, die weder unbeobachtete Taxa berücksichtigen noch Varianzschätzungen liefern, deutlich vorzuziehen.
Diskussion
Plug-in-Schätzungen vieler Alpha-Diversitäts-Indizes (einschließlich Richness und Shannon-Diversität) sind für den Alpha-Diversitäts-Parameter der Umgebung negativ verzerrt, das heißt, sie unterschätzen die wahre Alpha-Diversität (Lande, 1996). Der Versuch, dieses Problem mit Hilfe von Rarefaction zu lösen, führt tatsächlich zu einer größeren Verzerrung. Dies wird manchmal mit der Behauptung gerechtfertigt, dass verdünnte Schätzungen gleichermaßen verzerrt sind. Dies ist jedoch nicht generell wahr, da Umgebungen in Bezug auf eine Alpha-Diversitäts-Metrik identisch sein können, aber die unterschiedlichen Abundanzstrukturen unterschiedliche Verzerrungen verursachen, wenn sie verdünnt werden. Abbildung 1E zeigt beispielsweise zwei Umgebungen mit unterschiedlichen Abundanzstrukturen, aber gleichem Reichtum; die Rarefizierung vermittelt den falschen Eindruck eines ungleichen Reichtums (siehe auch Lande et al., 2000). Auf diese Weise werden sowohl der Probenreichtum als auch der Rarefied Richness durch Artefakte des Experiments (Bibliotheksgröße) und nicht durch die reine Struktur der mikrobiellen Gemeinschaft bestimmt. Um aussagekräftige Schlussfolgerungen über die gesamte mikrobielle Gemeinschaft zu ziehen, ist es notwendig, die unvollständige Probenahme durch statistisch motivierte Parameterschätzungen für die Alpha-Diversität zu korrigieren. Um aussagekräftige Schlussfolgerungen bezüglich des Vergleichs von mikrobiellen Gemeinschaften zu ziehen, ist es notwendig, Messfehlermodelle zu verwenden, um die Unsicherheit bei der Schätzung der Alpha-Diversität zu bereinigen.
Kürzlich wurde argumentiert, dass das Studium der mikrobiellen Diversität ohne Kontext uns davon ablenkt, Einblicke in ökologische Mechanismen zu gewinnen (Shade, 2016). Zu dieser Kritik füge ich hinzu, dass die falsche Anwendung statistischer Werkzeuge viele Analysen der Alpha-Diversität untergräbt. Ich ermutige mikrobielle Ökologen, Schätzungen der Alpha-Diversität zu verwenden, die unbeobachtete Arten berücksichtigen, und die Varianz der Schätzungen in Messfehlermodellen zu verwenden, um die Diversität über Ökosysteme hinweg zu vergleichen.
Beiträge der Autoren
AW schrieb das Manuskript und führte die Datenanalyse durch.
Finanzierung
AW wird durch Start-up-Mittel unterstützt, die von der Abteilung für Biostatistik an der University of Washington und den National Institutes of Health (R35GM133420) vergeben wurden.
Interessenkonflikt
Der Autor erklärt, dass die Forschung in Abwesenheit jeglicher kommerzieller oder finanzieller Beziehungen durchgeführt wurde, die als potenzieller Interessenkonflikt ausgelegt werden könnten.
Danksagungen
Dieser Artikel basiert auf Kursnotizen, die der Autor am Marine Biological Laboratory im Rahmen des STAMPS-Kurses in den Jahren 2013, 2014, 2015, 2016, 2017 und 2018 präsentiert hat. Der Autor bedankt sich bei Berry Brosi, dem MBL, den STAMPS-Kursleitern und den STAMPS-Teilnehmern für unzählige Diskussionen zu diesem Thema. Der Autor dankt auch Thea Whitman und zwei Gutachtern für viele durchdachte Vorschläge zum Manuskript. Dieses Manuskript wurde als Preprint über bioRxiv (Willis, 2017) veröffentlicht.
Arbel, J., Mengersen, K., und Rousseau, J. (2016). Bayesianisches nichtparametrisches abhängiges Modell für partiell replizierte Daten: der Einfluss von Treibstoffverschmutzungen auf die Artenvielfalt. Ann. Appl. Stat. 10, 1496-1516. doi: 10.1214/16-AOAS944
CrossRef Full Text | Google Scholar
Arora, T., Seyfried, F., Docherty, N. G., Tremaroli, V., le Roux, C. W., Perkins, R., et al. (2017). Diabetes-assoziierte Mikrobiota in fa/fa Ratten wird durch Roux-en-Y Magenbypass modifiziert. ISME J. 11, 2035-2046. doi: 10.1038/ismej.2017.70
PubMed Abstract | CrossRef Full Text | Google Scholar
Bunge, J., Willis, A., and Walsh, F. (2014). Schätzung der Anzahl der Arten in mikrobiellen Diversitätsstudien. Annu. Rev. Stat. Appl. 1, 427-445. doi: 10.1146/annurev-statistics-022513-115654
CrossRef Full Text | Google Scholar
Chao, A., and Bunge, J. (2002). Estimating the number of species in a stochastic abundance model. Biometrics 58, 531-539. doi: 10.1111/j.0006-341X.2002.00531.x
PubMed Abstract | CrossRef Full Text | Google Scholar
Chao, A., and Shen, T.-J. (2003). Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environ. Ecol. Stat. 10, 429-443. doi: 10.1023/A:1026096204727
CrossRef Full Text | Google Scholar
Demidenko, E. (2004). Mixed Models: Theory and Applications. Hoboken, NJ: Wiley-Interscience. doi: 10.1002/0471728438
CrossRef Full Text | Google Scholar
Fisher, R. A., Corbet, A. S., and Williams, C. B. (1943). Die Beziehung zwischen der Anzahl der Arten und der Anzahl der Individuen in einer Stichprobe einer Tierpopulation. J. Anim. Ecol. 12:42. doi: 10.2307/1411
CrossRef Full Text | Google Scholar
Hurlbert, S. H. (1971). Das Nicht-Konzept der Artenvielfalt: eine Kritik und alternative Parameter. Ecology 52, 577-586. doi: 10.2307/1934145
PubMed Abstract | CrossRef Full Text | Google Scholar
Lande, R. (1996). Statistik und Partitionierung der Artenvielfalt und der Ähnlichkeit zwischen verschiedenen Gemeinschaften. Oikos 76, 5-13. doi: 10.2307/3545743
CrossRef Full Text | Google Scholar
Lande, R., DeVries, P. J., and Walla, T. R. (2000). When species accumulation curves intersect: implications for ranking diversity using small samples. Oikos 89, 601-605. doi: 10.1034/j.1600-0706.2000.890320.x
CrossRef Full Text | Google Scholar
Makipaa, R., Rajala, T., Schigel, D., Rinne, K. T., Pennanen, T., Abrego, N., et al. (2017). Interaktionen zwischen boden- und totholzbewohnenden Pilzgemeinschaften während der Zersetzung von Fichtenstämmen. ISME J. 11, 1964-1974. doi: 10.1038/ismej.2017.57
PubMed Abstract | CrossRef Full Text | Google Scholar
McMurdie, P. J., and Holmes, S. (2014). Waste not, want not: why rarefying microbiome data is inadmissible. PLoS Comput. Biol. 10:e1003531. doi: 10.1371/journal.pcbi.1003531
CrossRef Full Text | Google Scholar
Sanders, H. L. (1968). Marine benthische Diversität: eine vergleichende Studie. Am. Nat. 102, 243-282. doi: 10.1086/282541
CrossRef Full Text | Google Scholar
Shade, A. (2016). Diversity is the question, not the answer. ISME J. 11, 1-6. doi: 10.1038/ismej.2016.118
CrossRef Full Text | Google Scholar
Shannon, C. E. (1948). Eine mathematische Theorie der Kommunikation. Bell Syst. Tech. J. 27, 379-423. doi: 10.1002/j.1538-7305.1948.tb01338.x
CrossRef Full Text | Google Scholar
Simpson, E. H. (1949). Measurement of diversity. Nature 163:688. doi: 10.1038/163688a0
CrossRef Full Text | Google Scholar
Washburne, A. D., Morton, J. T., Sanders, J., McDonald, D., Zhu, Q., Oliverio, A. M., et al. (2018). Methoden zur phylogenetischen Analyse von Mikrobiomdaten. Nat. Microbiol. 3:652. doi: 10.1038/s41564-018-0156-0
PubMed Abstract | CrossRef Full Text | Google Scholar
Weiss, S., Xu, Z. Z., Peddada, S., Amir, A., Bittinger, K., Gonzalez, A., et al. (2017). Normalisierung und mikrobielle differentielle Abundanz-Strategien hängen von den Dateneigenschaften ab. Microbiome 5:27. doi: 10.1186/s40168-017-0237-y
PubMed Abstract | CrossRef Full Text | Google Scholar
Willis, A. (2017). Rarefaction, alpha diversity, and statistics. bioRxiv 1-8. doi: 10.1101/231878
CrossRef Full Text | Google Scholar
Willis, A., and Bunge, J. (2015). Estimating diversity via frequency ratios. Biometrics 71, 1042-1049. doi: 10.1111/biom.12332
PubMed Abstract | CrossRef Full Text | Google Scholar
Willis, A. D., Bunge, J., and Whitman, T. (2016). Verbesserte Erkennung von Änderungen des Artenreichtums in mikrobiellen Gemeinschaften mit hoher Diversität. J. R. Stat. Soc. C Appl. Stat. 66, 963-977. doi: 10.1111/rssc.12206
CrossRef Full Text | Google Scholar
Willis, A. D., and Martin, B. D. (2018). Divnet: estimating diversity in networked communities. bioRxiv 1-23. doi: 10.1101/305045
CrossRef Full Text | Google Scholar
Zhang, Z., and Grabchak, M. (2016). Entropische Darstellung und Schätzung von Diversitätsindizes. J. Nonparametr. Stat. 28, 563-575. doi: 10.1080/10485252.2016.1190357
CrossRef Full Text | Google Scholar