Goodness of Fit Test: Was ist das?

Statistik-Definitionen > Goodness-of-Fit-Tests

Der Goodness-of-Fit-Test wird verwendet, um zu testen, ob Stichprobendaten zu einer Verteilung aus einer bestimmten Population passen (d.d. h. einer Population mit einer Normalverteilung oder einer mit einer Weibull-Verteilung). Mit anderen Worten, er sagt Ihnen, ob Ihre Stichprobendaten die Daten repräsentieren, die Sie in der tatsächlichen Population zu finden erwarten würden. In der Statistik häufig verwendete Anpassungsgüte-Tests sind:

• Das Chi-Quadrat.
• Kolmogorov-Smirnov.
• Anderson-Darling.
• Shipiro-Wilk.

Der Chi-Quadrat-Test der Anpassungsgüte

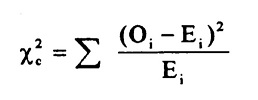
Die Chi-Quadrat-Formel.

Der Chi-Quadrat-Test ist der gebräuchlichste der Anpassungsgüte-Tests und ist derjenige, dem Sie in AP-Statistik oder elementarer Statistik begegnen werden. Der Chi-Quadrat-Test kann für diskrete Verteilungen wie die Binomialverteilung und die Poisson-Verteilung verwendet werden, während die Kolmogorov-Smirnov- und Anderson-Darling-Anpassungstests nur für kontinuierliche Verteilungen verwendet werden können.

Zwei mögliche Nachteile des Chi-Quadrat-Tests sind:

1. Der Chi-Quadrat-Test kann nur für Daten verwendet werden, die in Klassen (Bins) eingeteilt sind. Wenn Sie Daten haben, die nicht in Klassen eingeteilt sind, müssen Sie eine Häufigkeitstabelle oder ein Histogramm erstellen, bevor Sie den Test durchführen.
2. Ein weiterer Nachteil des Chi-Quadrat-Tests ist, dass er einen ausreichenden Stichprobenumfang erfordert, damit die Chi-Quadrat-Näherung gültig ist.

Es gibt noch eine andere Art von Chi-Quadrat-Test, den Chi-Quadrat-Test auf Unabhängigkeit. Die beiden werden manchmal verwechselt, aber sie sind recht unterschiedlich.

• Der Chi-Quadrat-Test auf Unabhängigkeit vergleicht zwei Datensätze, um zu sehen, ob eine Beziehung besteht.
• Der Chi-Quadrat-Goodness-of-Fit-Test dient dazu, eine kategoriale Variable an eine Verteilung anzupassen.

Beide Tests verwenden die Chi-Quadrat-Statistik und die Verteilung. Weitere Informationen zur Berechnung der Chi-Quadrat-Statistik finden Sie unter:
Die Chi-Quadrat-Teststatistik (einschließlich Berechnungen): Was ist eine Chi-Quadrat-Statistik?

Ausführung des Tests

Typischerweise wird dieser Test mithilfe einer Software ausgeführt. Die Nullhypothese für den Chi-Quadrat-Anpassungstest ist, dass die Daten aus einer bestimmten Verteilung stammen. Die Alternativhypothese ist, dass die Daten nicht aus einer bestimmten Verteilung stammen.

Um den Test zu interpretieren, müssen Sie ein Alpha-Niveau wählen (1%, 5% und 10% sind üblich). Der Chi-Quadrat-Test gibt einen p-Wert zurück. Wenn der p-Wert klein ist (kleiner als das Signifikanzniveau), können Sie die Nullhypothese, dass die Daten aus der angegebenen Verteilung stammen, zurückweisen.

Weniger gebräuchliche Anpassungsgütetests in der elementaren Statistik

Kolmogorov-Smirnov

Obwohl dieser Test als Normalitätstest bezeichnet wird, sagt er nicht aus, ob eine bestimmte Stichprobe wahrscheinlich aus einer normalen Population stammt. Stattdessen sagt er Ihnen, wann es unwahrscheinlich ist, dass es sich um eine Normalverteilung handelt. Ein Vorteil dieses Tests ist, dass er keine Annahmen über die Verteilung der Daten macht. Eine Stichprobe kann mit einer Verteilung verglichen werden, indem ein K-S-Test für eine Stichprobe oder ein K-S-Test für zwei Stichproben verwendet wird. Der Test wird in der Regel mit einer Software (wie SPSS) durchgeführt, da die kritischen Werte für jede Verteilung berechnet werden müssen und das Auffinden der Tabellen mit den kritischen Werten keine einfache Aufgabe ist. Der Test wird normalerweise für große Stichproben über 2000 empfohlen. Für kleinere Stichproben verwenden Sie Shapiro-Wilk.

Anderson-Darling

Dieser Test ist eine Modifikation von Kolmogorov-Smirnov. Er ist empfindlicher gegenüber Abweichungen in den Schwänzen einer Verteilung. Wie der Kolmogorov-Smirnov-Test zeigt dieser Test an, wann es unwahrscheinlich ist, dass eine Normalverteilung vorliegt und wird normalerweise mit statistischer Software durchgeführt.

Shapiro-Wilk

Dieser Test berechnet einen W-Wert, der Ihnen sagt, ob eine Stichprobe aus einer normalverteilten Population stammt. Der Test wird für Stichproben bis zu n=2000 empfohlen.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, S. 536 und 571, 2002.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf dem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!