Grundlagen der Graphendarstellung Exponentialfunktionen
Die Exponentialfunktion y=b^x mit b>0 ist eine Funktion, die bei Wachstum oder Zerfall proportional zu ihrem Ausgangswert bleibt.
Lernziele
Beschreiben Sie die Eigenschaften der Graphen von Exponentialfunktionen
Key Takeaways
Key Points
- Wenn die Basis b größer als 1 ist, dann wächst die Funktion exponentiell mit einer Wachstumsrate von b. Dies wird als exponentielles Wachstum bezeichnet.
- Wenn die Basis, b, kleiner als 1 (aber größer als 0) ist, dann fällt die Funktion exponentiell mit einer Rate von b. Dies wird als exponentieller Zerfall bezeichnet.
- Wenn die Basis, b, gleich 1 ist, dann wird die Funktion trivialerweise y=a.
- Die Punkte (0,1) und (1,b) liegen immer auf dem Graphen der Funktion y=b^x
- Die Funktion y=b^x nimmt nur positive Werte an und hat die x-Achse als horizontale Asymptote.
Schlüsselbegriffe
- Exponentialwachstum: Das Wachstum des Wertes einer Menge, bei dem die Wachstumsrate proportional zum momentanen Wert der Menge ist; wenn sich z. B. der Wert verdoppelt hat, hat sich auch die Wachstumsrate verdoppelt. Die Rate kann positiv oder negativ sein. Wenn sie negativ ist, wird sie auch als exponentieller Zerfall bezeichnet.
- Asymptote: Eine Linie, der sich eine Kurve beliebig stark nähert. Eine Asymptote kann vertikal, schräg oder horizontal sein. Horizontale Asymptoten entsprechen dem Wert, dem sich die Kurve nähert, wenn x sehr groß oder sehr klein wird.
- Exponentialfunktion: Jede Funktion, in der eine unabhängige Variable in Form eines Exponenten auftritt; sie sind die Umkehrfunktionen von Logarithmen.
Definitionen
Auf der grundlegendsten Ebene ist eine Exponentialfunktion eine Funktion, in der die Variable im Exponenten erscheint. Die grundlegendste Exponentialfunktion ist eine Funktion der Form y=b^x, wobei b eine positive Zahl ist.
Wenn b>1 ist, wächst die Funktion auf eine Weise, die proportional zu ihrem ursprünglichen Wert ist. Dies nennt man exponentielles Wachstum.
Wenn 0>b>1 ist, zerfällt die Funktion proportional zu ihrem Ausgangswert. Dies wird als exponentieller Zerfall bezeichnet.
Grafik einer Exponentialfunktion
Betrachten wir die Funktion y=2^x, wenn b>1. Eine Möglichkeit, diese Funktion grafisch darzustellen, besteht darin, Werte für x zu wählen und diese in die Gleichung einzusetzen, um Werte für y zu erzeugen. Auf diese Weise erhalten wir die folgenden Punkte:
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) und (2,4)
Wenn Sie die Punkte verbinden, werden Sie eine glatte Kurve bemerken, die die y-Achse im Punkt (0,1) schneidet und ansteigt, wenn x immer größere Werte annimmt. Das heißt, die Kurve nähert sich der Unendlichkeit, wenn x sich der Unendlichkeit nähert. Wenn x immer kleinere Werte annimmt, nähert sich die Kurve immer mehr der x-Achse. Das heißt, die Kurve nähert sich dem Nullpunkt, wenn sich x dem negativen Unendlichen nähert, so dass die x-Achse eine horizontale Asymptote der Funktion ist. Der Punkt (1,b) liegt auf dem Graphen. Dies gilt für den Graphen aller Exponentialfunktionen der Form y=b^x für x>1.

Graph von y=2^x: Der Graph dieser Funktion kreuzt die y-Achse bei (0,1) und nimmt zu, wenn sich x dem Unendlichen nähert. Die x-Achse ist eine horizontale Asymptote der Funktion.
Beispiel 2
Betrachten wir die Funktion y=\frac{1}{2}^x bei 0<b<1. Eine Möglichkeit, diese Funktion grafisch darzustellen, besteht darin, Werte für x zu wählen und diese in die Gleichung einzusetzen, um Werte für y zu erzeugen. Auf diese Weise erhalten Sie die folgenden Punkte:
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) und (2,\frac{1}{4})
Wenn Sie die Punkte verbinden, werden Sie eine glatte Kurve feststellen, die die y-Achse im Punkt (0,1) schneidet und abnimmt, wenn x größere und größere Werte annimmt. Die Kurve nähert sich bei Annäherung an Unendlich dem Wert Null. Da x immer kleinere Werte annimmt, nähert sich die Kurve immer mehr der x -Achse. Das heißt, die Kurve nähert sich Null, wenn x sich dem negativen Unendlichen nähert, wodurch die x-Achse eine horizontale Asymptote der Funktion wird. Der Punkt (1,b) liegt auf dem Graphen. Dies gilt für den Graphen aller Exponentialfunktionen der Form y=b^x für 0<x<1.
Wie Sie in der Grafik unten sehen können, ist der Graph von y=\frac{1}{2}^x symmetrisch zu dem von y=2^x über der y-Achse. Das heißt, wenn die Ebene über die y-Achse gefaltet würde, würden die beiden Kurven aufeinander liegen.
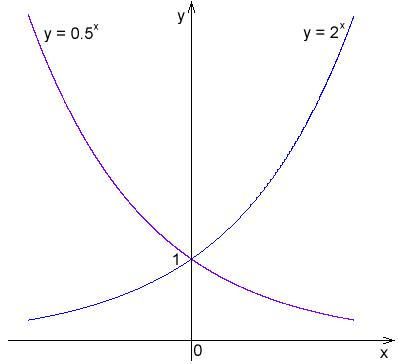
Graph von y=2^x und y=\frac{1}{2}^x: Die Graphen dieser Funktionen sind symmetrisch über der y-Achse.
Warum muss b eine positive Zahl sein?
Wenn b=1, dann wird die Funktion zu y=1^x. Da 1 zu einer beliebigen Potenz 1 ergibt, ist die Funktion äquivalent zu y=1, was eine horizontale Linie und keine Exponentialgleichung ist.
Wenn b negativ ist, dann ergibt das Erhöhen von b zu einer geraden Potenz einen positiven Wert für y, während das Erhöhen von b zu einer ungeraden Potenz einen negativen Wert für y ergibt, was es unmöglich macht, die erhaltenen Punkte auf irgendeine sinnvolle Weise zu verbinden und sicherlich nicht auf eine Weise, die eine Kurve wie in den obigen Beispielen erzeugt.
Eigenschaften von Exponentialgraphen
Der Punkt (0,1) liegt immer auf dem Graphen einer Exponentialfunktion der Form y=b^x, weil b positiv ist und jede positive Zahl hoch Null den Wert 1 ergibt.
Der Punkt (1,b) liegt immer auf dem Graphen einer Exponentialfunktion der Form y=b^x, weil jede positive Zahl b in der ersten Potenz 1 ergibt.
Die Funktion y=b^x nimmt nur positive Werte an, weil jede positive Zahl b in jeder Potenz nur positive Werte ergibt.
Die Funktion y=b^x hat die x-Achse als horizontale Asymptote, weil sich die Kurve immer der x-Achse nähert, wenn sich x entweder dem positiven oder dem negativen Unendlichen nähert, aber niemals die Achse schneidet, da sie niemals gleich Null sein wird.
Graphen von logarithmischen Funktionen
Logarithmische Funktionen können manuell oder elektronisch grafisch dargestellt werden, wobei die Punkte im Allgemeinen mit einem Taschenrechner oder einer Tabelle bestimmt werden.
Lernziele
Beschreiben Sie die Eigenschaften von Graphen logarithmischer Funktionen
Key Takeaways
Key Points
- Die logarithmische Funktion hat eine ähnliche Form wie die Quadratwurzelfunktion, jedoch mit einer vertikalen Asymptote, wenn sich x von rechts 0 nähert.
- Der Punkt (1,0) liegt auf dem Graphen aller logarithmischen Funktionen der Form y=log{_b}x, wobei b eine positive reelle Zahl ist.
- Der Bereich der logarithmischen Funktion y=log{_b}x, wobei b eine positive reelle Zahl ist, ist die Menge aller positiven reellen Zahlen, während der Bereich dieser Funktion alle reellen Zahlen sind.
- Der Graph einer logarithmischen Funktion der Form y=log{_b}x kann durch Addition einer Konstanten zur Variablen x bzw. zu y horizontal und/oder vertikal verschoben werden.
- Eine logarithmische Funktion der Form y=log{_b}x, wobei b eine positive reelle Zahl ist, kann mit Hilfe eines Taschenrechners dargestellt werden, um Punkte auf dem Graphen zu bestimmen, oder sie kann ohne Taschenrechner dargestellt werden, indem man die Tatsache nutzt, dass ihre Umkehrung eine Exponentialfunktion ist.
Schlüsselbegriffe
- Logarithmische Funktion: Jede Funktion, in der eine unabhängige Variable in Form eines Logarithmus auftritt. Die Umkehrung einer logarithmischen Funktion ist eine Exponentialfunktion und umgekehrt.
- Logarithmus: Der Logarithmus einer Zahl ist der Exponent, um den ein anderer fester Wert, die Basis, erhöht werden muss, um diese Zahl zu erzeugen.
- Asymptote: Eine Linie, der sich eine Kurve willkürlich stark nähert. Asymptoten können horizontal, vertikal oder schräg sein.
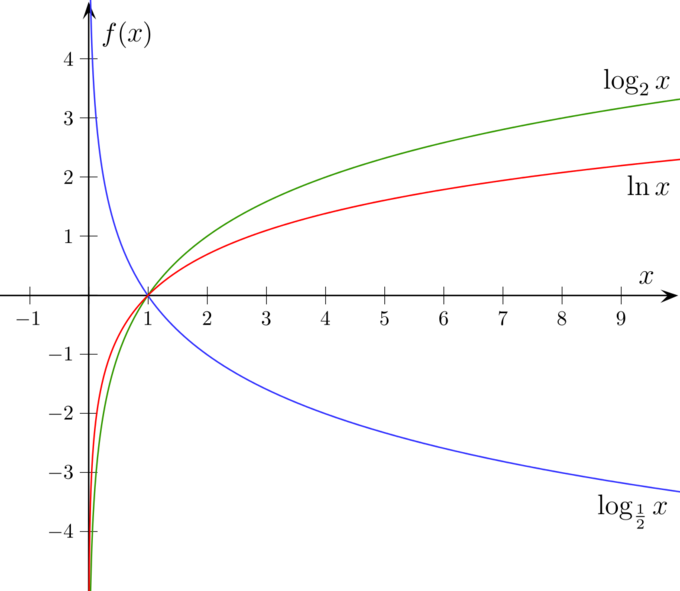
Unten sind Graphen von logarithmischen Funktionen mit den Basen 2, e und 10.

Logarithmische Graphen: Nach x=1, wo die Graphen die x-Achse kreuzen, liegt \log_2(x) in rot über \log_e(x) in grün, das über \log_{10}(x) in blau liegt. Vor diesem Punkt ist die Reihenfolge vertauscht. Alle drei Logarithmen haben die y-Achse als vertikale Asymptote und sind immer steigend.
Alle drei logarithmischen Graphen beginnen mit einem steilen Anstieg nach x=0, dehnen sich aber immer mehr horizontal aus, wobei ihre Steigung mit zunehmendem x immer geringer wird. Alle schneiden die x-Achse bei x=1.
Eigenschaften der Graphen logarithmischer Funktionen
Der Graph schneidet die x-Achse bei 1. Das heißt, der Graph hat einen x-Achsenabschnitt von 1, und als solcher liegt der Punkt (1,0) auf dem Graph. Tatsächlich wird der Punkt (1,0) immer auf dem Graphen einer Funktion der Form y=log{_b}x liegen, wobei b>0 ist. Das liegt daran, dass für x=1 die Gleichung des Graphen y=log{_b}1 ist.
Wir suchen also nach einem solchen Exponenten y, dass b^y=1 ist. Da b>0 ist, ist der gesuchte Exponent 1, unabhängig vom Wert von b. Das bedeutet, dass der Punkt (x,y)=(1,0) immer auf einer logarithmischen Funktion dieses Typs liegen wird.
Asymptoten
Die y-Achse ist eine vertikale Asymptote des Graphen. Das bedeutet, dass sich die Kurve der y-Achse immer mehr annähert, sie aber nicht schneidet.
Betrachten wir, was passiert, wenn sich der Wert von x von rechts der Null nähert, für die Gleichung, deren Graph oben erscheint. Nämlich: y=log{_b}x. Wir können dies tun, indem wir Werte für x wählen, sie in die Gleichung einsetzen und Werte für y erzeugen.
Lassen Sie uns annehmen, dass b eine positive Zahl größer als 1 ist, und lassen Sie uns Werte für x zwischen 0 und 1 untersuchen. Wenn wir unter diesen Bedingungen x=\frac{1}{b} lassen, wird die Gleichung zu y=log\frac{1}{b}.
Wir suchen also nach einem solchen Exponenten, dass b erhöht auf diesen Exponenten \frac{1}{b} ergibt. Der gesuchte Exponent ist -1 und der Punkt (\frac{1}{b},-1) liegt auf dem Graphen. Auf ähnliche Weise erhalten wir die folgenden Punkte, die ebenfalls auf dem Graphen liegen:
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) und so weiter
Wenn wir Werte von x nehmen, die noch näher an 0 liegen, erhalten wir die folgenden Punkte: (\frac{1}{b^{10}},-10), (\frac{1}{b^{100}},-100) und (\frac{1}{b^{1000}},-1000)
Wie man sieht, wird der Graph immer negativer, je näher der Wert von x an 0 heranrückt. Das heißt, wenn x sich Null nähert, nähert sich der Graph der negativen Unendlichkeit. Das bedeutet, dass die y-Achse eine vertikale Asymptote der Funktion ist.
Domäne und Bereich
Die Domäne der Funktion sind alle positiven Zahlen. Das bedeutet, dass der x-Wert der Funktion immer positiv sein wird. Beginnen wir mit der Überlegung, warum der x-Wert der Kurve nie 0 ist.
Wäre der x-Wert Null, würde die Funktion y=log{_b}0 lauten.
Hier suchen wir einen Exponenten, so dass b erhöht auf diesen Exponenten 0 ist. Da b eine positive Zahl ist, gibt es keinen Exponenten, auf den wir b erhöhen können, um 0 zu erhalten. Da b positiv ist, ergibt das Erhöhen auf eine Potenz immer eine positive Zahl.
Der Bereich der Funktion sind alle reellen Zahlen. Das heißt, der Graph kann jede reelle Zahl annehmen.
Vergleich y=log{_x} und y=\sqrt{x}
Auf den ersten Blick kann der Graph der logarithmischen Funktion leicht mit dem der Quadratwurzelfunktion verwechselt werden.
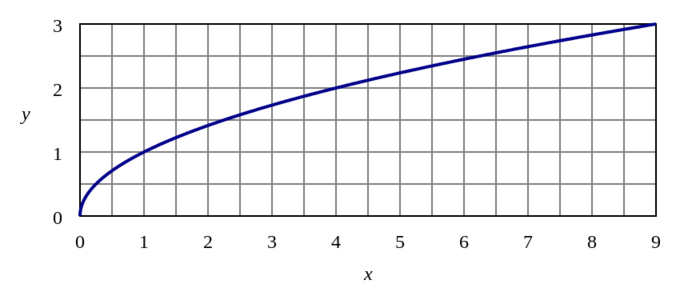
Graph von y=\sqrt{x}: Der Graph der Quadratwurzelfunktion ähnelt dem Graphen der logarithmischen Funktion, hat aber keine vertikale Asymptote.
Beide, die Quadratwurzel- und die logarithmische Funktion, haben einen Bereich, der auf x-Werte größer als 0 beschränkt ist. Die logarithmische Funktion hat jedoch eine vertikale Asymptote, die gegen -\infty abfällt, wenn x sich 0 nähert, während die Quadratwurzelfunktion einen minimalen y-Wert von 0 erreicht. Der Bereich der Quadratwurzelfunktion sind alle nichtnegativen reellen Zahlen, während der Bereich der logarithmischen Funktion alle reellen Zahlen sind.
Grafische Darstellung logarithmischer Funktionen
Die grafische Darstellung logarithmischer Funktionen kann durch das Auffinden von Punkten auf der Kurve entweder manuell oder mit einem Taschenrechner erfolgen.
Bei der grafischen Darstellung ohne Taschenrechner nutzen wir die Tatsache, dass die Inverse einer logarithmischen Funktion eine Exponentialfunktion ist.
Bei der grafischen Darstellung mit einem Taschenrechner nutzen wir die Tatsache, dass der Taschenrechner nur gewöhnliche Logarithmen (Basis ist 10), natürliche Logarithmen (Basis ist e) oder binäre Logarithmen (Basis ist 2) berechnen kann. Wenn wir einen grafischen Taschenrechner haben, kann der Rechner die Funktion natürlich auch grafisch darstellen, ohne dass wir Punkte auf dem Graphen finden müssen.
Grafische Darstellung logarithmischer Funktionen mit Hilfe ihrer Inversen
Logarithmische Funktionen können ohne die Verwendung eines Taschenrechners von Hand grafisch dargestellt werden, wenn wir die Tatsache nutzen, dass sie Inverse von Exponentialfunktionen sind.
Betrachten wir wieder den Graphen der folgenden Funktion:
y=log{_3}x
Diese lässt sich in Exponentialform schreiben als:
3^y=x
Nun betrachten wir die Inverse dieser Funktion. Dazu vertauschen wir x und y:
3^x=y
Die Exponentialfunktion 3^x=y ist eine, für die wir leicht Punkte erzeugen können. Wenn wir einige Werte für x nehmen und sie in die Gleichung einsetzen, um die entsprechenden Werte für y zu finden, erhalten wir die folgenden Punkte:
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) und (3,27)
Nun müssen wir beachten, dass diese Punkte nicht auf der ursprünglichen Funktion (y=log{_3}x) liegen, sondern auf ihrer Umkehrung 3^x=y. Wenn wir jedoch die x- und y-Koordinaten der einzelnen Punkte vertauschen, erhalten wir tatsächlich eine Liste von Punkten auf der ursprünglichen Funktion.
Diese sind: (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) und (27,3).
Wir plotten und verbinden diese Punkte, um den Graphen der Funktion y=log{_3}x unten zu erhalten.

Graph von y=log{_3}x: Der Graph der logarithmischen Funktion zur Basis 3 kann mit der Umkehrfunktion der Funktion erzeugt werden. Seine Form ist die gleiche wie bei anderen logarithmischen Funktionen, nur mit einem anderen Maßstab.
Grafik von logarithmischen Funktionen mit Basen zwischen 0 und 1
Bislang haben wir logarithmische Funktionen gezeichnet, deren Basen größer als 1 sind. Wenn wir stattdessen logarithmische Funktionen mit einer Basis b betrachten, so dass 0<b<1 ist, erhalten wir einen Graphen, der denen sehr ähnlich ist, die wir bereits gesehen haben.
Wenn b>0 ist, sind der Graph von y=log{_b}x und der Graph von y=log{_\frac{1}{b}}x symmetrisch über der x-Achse. Wenn wir also einen Punkt (x,y) auf dem Graphen von y=log{_b}x identifizieren, können wir den entsprechenden Punkt auf y=log{_\frac{1}{b}}x finden, indem wir das Vorzeichen der y-Koordinate ändern. Der entsprechende Punkt ist (x,-y).
Hier ist ein Beispiel für b=2.
Graphen von log{_2}x und log{_\frac{1}{2}}x : Die Graphen von log_2 x und log{_\frac{1}{2}}x sind symmetrisch über der x-Achse
Problemlösung mit logarithmischen Graphen
Einige Funktionen mit sich schnell ändernder Form lassen sich am besten auf einer exponentiell ansteigenden Skala darstellen, wie z. B. ein logarithmischer Graph.
Lernziele
Konvertieren Sie Probleme in logarithmische Skalen und diskutieren Sie die Vorteile, die sich daraus ergeben
Key Takeaways
Key Points
- Logarithmische Graphen verwenden logarithmische Skalen, bei denen sich die Werte exponentiell unterscheiden. Anstelle von Markierungen bei 0, 1, 2 und 3 kann eine logarithmische Skala z. B. Markierungen bei 0,1, 1, 10 und 100 enthalten, die jeweils den gleichen Abstand zum vorherigen und nächsten Wert haben.
- Logarithmische Graphen ermöglichen es, einen sehr großen Bereich von Daten darzustellen, ohne dass die Form des Graphen verloren geht.
- Logarithmische Graphen erleichtern die Interpolation in Bereichen, die auf linearen Achsen schwer ablesbar sind. Wenn z. B. das Diagramm y=x^5 so skaliert ist, dass es einen sehr großen Bereich von y-Werten zeigt, kann die Krümmung in der Nähe des Ursprungs auf linearen Achsen ununterscheidbar sein. Auf logarithmischen Achsen ist sie viel deutlicher.
Schlüsselbegriffe
- Logarithmus: Der Logarithmus einer Zahl ist der Exponent, um den ein anderer fester Wert, die Basis, erhöht werden muss, um diese Zahl zu erzeugen.
- Interpolieren: Abschätzung des Wertes einer Funktion zwischen zwei Punkten, zwischen denen sie tabelliert ist.
Warum eine logarithmische Skala verwenden?
Viele mathematische und physikalische Zusammenhänge sind funktional abhängig von Variablen höherer Ordnung. Das bedeutet, dass es bei kleinen Änderungen der unabhängigen Variablen zu sehr großen Änderungen der abhängigen Variablen kommt. Dadurch wird es schwierig, solche Funktionen auf der Standardachse darzustellen.
Betrachten wir als Beispiel das Stefan-Boltzmann-Gesetz, das die von einem schwarzen Körper abgestrahlte Leistung (j*) mit der Temperatur (T) in Beziehung setzt.
j^*= \sigma T^4
Auf einer Standardgrafik kann diese Gleichung ziemlich unhandlich sein. Die Abhängigkeit von der Temperatur vierten Grades bedeutet, dass die Leistung extrem schnell ansteigt. Die Tatsache, dass die Rate stetig (und steil) ansteigt, bedeutet, dass eine Änderung der Skalierung (Skalierung der Achsen um 5, 10 oder sogar 100) wenig hilfreich ist, um den Graphen einfacher zu interpretieren.
Für sehr steile Funktionen ist es möglich, Punkte glatter darzustellen und dabei die Integrität der Daten beizubehalten: Man kann einen Graphen mit einer logarithmischen Skala verwenden, bei der jede Stelle des Graphen nicht einen konstanten Anstieg, sondern einen exponentiellen Anstieg darstellt. Wo ein normaler (linearer) Graph gleiche Intervalle hat, die 1, 2, 3, 4 gehen, würden bei einer logarithmischen Skala dieselben gleichen Intervalle 1, 10, 100, 1000 darstellen. Hier sind einige Beispiele von Funktionen, die auf einer linearen, halblogarithmischen und logarithmischen Skala dargestellt sind.
Die obere linke Seite ist eine lineare Skala. Die untere rechte ist eine logarithmische Skala. Oben rechts und unten links werden halblogarithmische Skalen genannt, weil eine Achse linear skaliert wird, während die andere mit Logarithmen skaliert wird.

Logarithmische Skala: Die Graphen der Funktionen f(x)=10^x,f(x)=x und f(x)=\log x auf vier verschiedenen Koordinatenplots. Oben links ist eine lineare Skala, oben rechts und unten links sind halblogarithmische Skalen und unten rechts ist eine logarithmische Skala.
Wie Sie sehen, behielt der Graph die Eigenschaften des ursprünglichen Graphen (oben links), bei dem beide Achsen mit einer linearen Skala skaliert wurden, bei, wenn beide Achsen eine logarithmische Skala verwendeten (unten rechts). Das bedeutet, wenn wir eine Funktion grafisch darstellen wollen, die auf einer linearen Skala unhandlich ist, können wir eine logarithmische Skala auf jeder Achse verwenden und die Eigenschaften des Graphen beibehalten, während wir ihn gleichzeitig einfacher grafisch darstellen können.
Bei den halblogarithmischen Skalen haben die Funktionen Formen, die im Vergleich zum Original schief sind. Wenn nur die x-Achse eine logarithmische Skala hat, erscheint die logarithmische Kurve als Linie und die lineare und exponentielle Kurve sehen beide exponentiell aus. Wenn nur die y-Achse eine logarithmische Skala hat, erscheint die exponentielle Kurve als Linie und die lineare und die logarithmische Kurve sehen beide logarithmisch aus.
Es sei darauf hingewiesen, dass die Beispiele in den Diagrammen zur Veranschaulichung gedacht waren und dass die dargestellten Funktionen auf einem linear skalierten Achsensatz nicht unbedingt unhandlich waren.
Umwandlung von linearen in logarithmische Skalen
Der Hauptunterschied zwischen logarithmischen und linearen Skalen besteht darin, dass, während die Wertedifferenz zwischen linearen Punkten mit gleichem Abstand konstant bleibt (d.h. wenn der Abstand von 0 bis 1 auf der Skala 1 cm beträgt, ist der Abstand von 1 bis 2, 2 bis 3, etc, gleich ist), ändert sich der Wertunterschied zwischen Punkten auf einer logarithmischen Skala exponentiell. Eine logarithmische Skala beginnt bei einer bestimmten Potenz von 10 und nimmt mit jeder Einheit um eine Potenz von 10 zu.
Wenn man also eine lineare Skala (mit den Werten 0-5) in eine logarithmische Skala umwandeln wollte, wäre eine Möglichkeit, 1,2,3,4 und 5 durch 0,001,0,01,0,1,1,10 bzw. 100 zu ersetzen. Zwischen jedem größeren Wert auf der logarithmischen Skala rücken die Rauten mit zunehmendem Wert immer näher zusammen. Zum Beispiel liegen im Bereich zwischen 1 und 10 die 8 und die 9 viel näher beieinander als die 2 und die 3.
Die Vorteile der Verwendung einer logarithmischen Skala sind zweierlei. Erstens kann man auf diese Weise einen sehr großen Bereich von Daten darstellen, ohne dass die Form des Graphen verloren geht. Zweitens ist es möglich, an jedem beliebigen Punkt des Diagramms zu interpolieren, unabhängig vom Bereich des Diagramms. Ähnliche Daten, die auf einer linearen Skala gezeichnet werden, sind weniger klar.
Problemlösung mit logarithmischen Graphen
Ein wichtiger Punkt bei der Verwendung von logarithmischen Graphen zur Problemlösung ist, dass sie die Skalen auf den Punkt erweitern, an dem große Datenbereiche mehr Sinn ergeben. In der oben erwähnten Gleichung (j^*= \sigma T^4) würde das Auftragen von j gegen T die erwartete Kurve erzeugen, aber die Skala wäre so groß, dass winzige Änderungen unbemerkt bleiben und die großen Skaleneffekte der Beziehung die Grafik dominieren: Sie ist so groß, dass die „interessanten Bereiche“ nicht in einem lesbaren Maßstab auf das Papier passen würden.
Nimmt man den Logarithmus von jeder Seite der Gleichungen, so ergibt sich: logj=log{(\sigma\tau ) }^4 . Wir stützen uns nun auf die Eigenschaften von Logarithmen, um die Gleichung umzuschreiben.
Erinnern Sie sich an die folgenden Eigenschaften von Logarithmen:
\log(ab)=\log(a)+\log(b) \\log(a)^b=(b)\log(a)
Anhand der obigen Ausführungen wird unsere Gleichung zu:
\begin{align} \log j&=4\log{(\sigma\tau ) } \\ &=4\log{(\sigma)}+4\log{(\tau ) } \\ &=4\log{(\tau ) }+4\log{(\sigma)} \end{align}