Nach der Lektüre dieses Kapitels werden Sie in der Lage sein, Folgendes zu tun:
- Definieren Sie den Zufallsfehler und unterscheiden Sie ihn von der Verzerrung
- Illustrieren Sie den Zufallsfehler mit Beispielen
- Interpretieren Sie einen p-Wert
- Interpretieren Sie ein Konfidenzintervall
- Unterscheiden Sie zwischen statistischen Fehlern des Typs 1 und des Typs 2 und erklären Sie, wie sie auf epidemiologische Forschung zutreffen
- Beschreiben Sie, wie statistische Potenz die Forschung beeinflusst
In diesem Kapitel, werden wir den Zufallsfehler behandeln – woher er kommt, wie wir mit ihm umgehen und was er für die Epidemiologie bedeutet.
Zuallererst: Zufällige Fehler sind keine Verzerrungen. Bias ist ein systematischer Fehler und wird in Kapitel 6 näher behandelt.
Zufallsfehler ist genau das, wonach es klingt: Zufallsfehler in den Daten. Alle Daten enthalten zufällige Fehler, weil kein Messsystem perfekt ist. Das Ausmaß der zufälligen Fehler hängt zum einen von der Skala ab, auf der etwas gemessen wird (Fehler bei Messungen auf molekularer Ebene liegen in der Größenordnung von Nanometern, während Fehler bei der Messung der menschlichen Körpergröße wahrscheinlich in der Größenordnung von ein oder zwei Zentimetern liegen) und zum anderen von der Qualität der verwendeten Werkzeuge. Physik- und Chemielabore haben hochpräzise, teure Waagen, die Masse auf das nächste Gramm, Mikrogramm oder Nanogramm genau messen können, während die durchschnittliche Waage im Badezimmer eines Menschen wahrscheinlich auf ein halbes Pfund oder Pfund genau ist.
Um sich den Zufallsfehler zu vergegenwärtigen, stellen Sie sich vor, Sie backen einen Kuchen, für den Sie 6 Esslöffel Butter benötigen. Um die 6 Esslöffel Butter zu erhalten (ein Dreiviertel eines Sticks, wenn 4 Sticks in einem Pfund enthalten sind, wie es in den USA üblich ist), könnten Sie die Markierungen auf dem Wachspapier um den Stick herum verwenden, vorausgesetzt, sie sind korrekt ausgerichtet. Oder Sie könnten die Methode meiner Mutter anwenden, die darin besteht, das Stäbchen auszupacken, eine leichte Markierung an einer Stelle zu machen, die wie die Hälfte des Stäbchens aussieht, und dann auf drei Viertel zu kommen, indem Sie die Hälfte der einen Hälfte mit dem Auge abschätzen. Oder Sie können meine Methode anwenden, bei der Sie die Dreiviertelmarkierung von Anfang an anvisieren und dann abschneiden. Jede dieser „Mess“-Methoden wird Ihnen ungefähr 6 Esslöffel Butter liefern, was für das Backen eines Kuchens sicherlich gut genug ist, aber wahrscheinlich nicht genau 3 Unzen wert ist, wie viel 6 Esslöffel Butter in den USA wiegen. Das Ausmaß, in dem Sie dieses Mal etwas über 3 Unzen und das nächste Mal vielleicht etwas unter 3 Unzen liegen, verursacht einen zufälligen Fehler in Ihrer Messung der Butter. Wenn Sie immer unter- oder überschätzt hätten, wäre das eine Verzerrung – aber Ihre konstant unter- oder überschätzten Messungen würden in sich selbst einen Zufallsfehler enthalten.
Für jede gegebene Variable, die wir in der Epidemiologie messen wollen (z.B., Größe, GPA, Herzfrequenz, Anzahl der Arbeitsjahre in einer bestimmten Fabrik, Serumtriglyceridspiegel usw.), erwarten wir, dass es eine Variabilität in der Stichprobe gibt, d.h. wir erwarten nicht, dass jeder in der Population genau den gleichen Wert hat. Dies ist kein Zufallsfehler. Zufällige Fehler (und Verzerrungen) treten auf, wenn wir versuchen, diese Dinge zu messen. In der Tat beruht die Epidemiologie als Fachgebiet auf dieser inhärenten Variabilität. Wenn alle Menschen genau gleich wären, könnten wir nicht feststellen, welche Menschen ein höheres Risiko haben, eine bestimmte Krankheit zu entwickeln.
In der Epidemiologie beruhen unsere Messungen manchmal darauf, dass ein anderer Mensch als der Studienteilnehmer etwas an oder über den Teilnehmer misst. Beispiele hierfür sind gemessene Größe oder Gewicht, Blutdruck oder Serumcholesterin. Bei einigen dieser Messungen (z. B. Gewicht und Serumcholesterin) schleicht sich der Zufallsfehler aufgrund des verwendeten Instruments in die Daten ein – hier eine Waage, die wahrscheinlich eine Schwankung von einem halben Pfund aufweist, oder ein Labortest mit einer Fehlermarge von einigen Milligramm pro Deziliter. Bei anderen Messungen (z. B. Körpergröße und Blutdruck) ist der Messende selbst für den zufälligen Fehler verantwortlich, wie im Beispiel mit der Butter.
Allerdings beruhen viele unserer Messungen auf Selbstauskünften der Teilnehmer. Es gibt ganze Lehrbücher und Kurse, die sich mit der Gestaltung von Fragebögen befassen, und die Wissenschaft, die dahinter steckt, wie man mit Umfragemethoden die genauesten Daten von Menschen erhält, ist ziemlich gut. Das Pew Research Center bietet auf seiner Website eine schöne Einführung in die Fragebogengestaltung an.
Relevant für unsere Diskussion hier ist, dass zufällige Fehler auch in Fragebogendaten auftreten. Bei einigen Variablen wird es weniger zufällige Fehler geben als bei anderen (z.B. ist die selbst angegebene Rasse wahrscheinlich ziemlich genau), aber es wird immer noch welche geben – z.B. wenn Leute versehentlich das falsche Feld ankreuzen. Bei anderen Variablen wird es mehr Zufallsfehler geben (z. B. ungenaue Antworten auf Fragen wie „Wie oft haben Sie im letzten Jahr Reis gegessen?“). Eine gute Frage, die Sie sich stellen sollten, wenn Sie die Menge an Zufallsfehlern in einer aus einem Fragebogen abgeleiteten Variable in Betracht ziehen, ist: „Können die Leute mir das sagen?“ Die meisten Leute könnten Ihnen theoretisch sagen, wie viel Schlaf sie letzte Nacht hatten, aber sie würden sich schwer tun, Ihnen zu sagen, wie viel Schlaf sie in derselben Nacht vor einem Jahr hatten. Ob sie es Ihnen sagen oder nicht, ist eine andere Sache und berührt die Verzerrung (siehe Kapitel 6). Unabhängig davon nimmt der Zufallsfehler in Fragebogendaten zu, je geringer die Wahrscheinlichkeit ist, dass die Befragten eine Antwort geben können.
Quantifizierung des Zufallsfehlers
Während wir daran arbeiten können – und sollten -, den Zufallsfehler zu minimieren (Verwendung von qualitativ hochwertigen Instrumenten, Schulung des Personals in der Durchführung von Messungen, Entwicklung von guten Fragebögen usw.), kann er nie ganz ausgeschlossen werden. Glücklicherweise können wir die Statistik nutzen, um die zufälligen Fehler in einer Studie zu quantifizieren. Genau dafür ist die Statistik da. In diesem Buch werde ich nur einen kleinen Ausschnitt aus dem weiten Feld der Statistik behandeln: die Interpretation von p-Werten und Konfidenzintervallen (CI). Anstatt mich darauf zu konzentrieren, wie man sie berechnet, werde ich mich stattdessen darauf konzentrieren, was sie bedeuten (und was sie nicht bedeuten). Die Kenntnis von p-Werten und CIs ist ausreichend, um eine genaue Interpretation der Ergebnisse epidemiologischer Studien für Epidemiologie-Anfänger zu ermöglichen.
p-Werte
Bei der Durchführung wissenschaftlicher Forschung jeglicher Art, einschließlich der Epidemiologie, beginnt man mit einer Hypothese, die dann während der Durchführung der Studie getestet wird. Wenn wir zum Beispiel die durchschnittliche Körpergröße von Studenten untersuchen, könnte unsere Hypothese (normalerweise mit H1 angegeben) lauten, dass männliche Studenten im Durchschnitt größer sind als weibliche Studenten. Für statistische Testzwecke müssen wir unsere Hypothese jedoch in eine Nullhypothese umformulieren. In diesem Fall würde unsere Nullhypothese (normalerweise mit H0 bezeichnet) wie folgt lauten:
Wir würden dann unsere Studie durchführen, um diese Hypothese zu testen. Wir bestimmen zunächst die Zielpopulation (Studenten) und ziehen eine Stichprobe aus dieser Population. Dann messen wir die Körpergröße und das Geschlecht aller Personen in der Stichprobe und berechnen die durchschnittliche Körpergröße der Männer im Vergleich zur Körpergröße der Frauen. Anschließend führen wir einen statistischen Test durch, um die mittleren Größen in den beiden Gruppen zu vergleichen. Da es sich um eine kontinuierliche Variable (Höhe) handelt, die in 2 Gruppen (Männer und Frauen) gemessen wurde, würden wir einen t-Test verwenden, und die mit diesem Test berechnete t-Statistik hätte einen entsprechenden p-Wert, was uns wirklich interessiert.
Angenommen, in unserer Studie finden wir, dass die männlichen Studenten im Durchschnitt 1,80 m groß sind und bei den weiblichen Studenten beträgt die durchschnittliche Körpergröße 1,80 m (bei einer Differenz von 4 cm), und wir berechnen einen p-Wert von 0,04. Das bedeutet, wenn es wirklich keinen Unterschied in der durchschnittlichen Körpergröße zwischen männlichen und weiblichen Studenten gibt (d.h. wenn die Nullhypothese wahr ist) und wir die Studie wiederholen (bis hin zur Ziehung einer neuen Stichprobe aus der Population), besteht eine Wahrscheinlichkeit von 4 %, dass wir wieder einen Unterschied in der durchschnittlichen Körpergröße von 4 Zoll oder mehr finden.
Es gibt mehrere Implikationen, die sich aus dem obigen Absatz ergeben. Erstens berechnen wir in der Epidemiologie immer 2-tailed p-values. Hier bedeutet dies einfach, dass die 4%ige Chance eines ≥4 Zoll Größenunterschieds nichts darüber aussagt, welche Gruppe größer ist – nur, dass eine Gruppe (entweder Männer oder Frauen) im Durchschnitt um mindestens 4 Zoll größer sein wird. Zweitens sind p-Werte bedeutungslos, wenn Sie zufällig in der Lage sind, die gesamte Bevölkerung in Ihre Studie einzuschließen. Ein Beispiel: Unsere Forschungsfrage bezieht sich auf Studenten in Public Health 425 (H425, Grundlagen der Epidemiologie) im Wintersemester 2020 an der Oregon State University (OSU). Sind Männer oder Frauen in dieser Population größer? Da die Population recht klein ist und alle Mitglieder leicht zu identifizieren sind, können wir alle einschließen, anstatt uns auf eine Stichprobe verlassen zu müssen. Es wird immer noch einen Zufallsfehler bei der Messung der Körpergröße geben, aber wir verwenden keinen p-Wert mehr, um diesen zu quantifizieren. Das liegt daran, dass wir bei einer Wiederholung der Studie genau das Gleiche herausfinden würden, da wir tatsächlich jeden in der Population gemessen haben. P-Werte gelten nur, wenn wir mit Stichproben arbeiten.
Schließlich ist zu beachten, dass der p-Wert die Wahrscheinlichkeit Ihrer Daten beschreibt, unter der Annahme, dass die Nullhypothese wahr ist – er beschreibt nicht die Wahrscheinlichkeit, dass die Nullhypothese angesichts Ihrer Daten wahr ist. Dies ist ein häufiger Interpretationsfehler, der sowohl von Anfängern als auch von erfahrenen Lesern von epidemiologischen Studien gemacht wird. Der p-Wert sagt nichts darüber aus, wie wahrscheinlich es ist, dass die Nullhypothese wahr ist (und damit im Umkehrschluss über den Wahrheitsgehalt Ihrer eigentlichen Hypothese). Vielmehr quantifiziert er die Wahrscheinlichkeit, die Daten zu erhalten, die Sie erhalten haben, wenn die Nullhypothese tatsächlich wahr ist. Dies ist ein feiner Unterschied, aber ein sehr wichtiger.
Statistische Signifikanz
Was passiert als nächstes? Wir haben einen p-Wert, der uns sagt, wie groß die Chance ist, dass unsere Daten bei der Nullhypothese wahr sind. Aber was bedeutet das eigentlich im Hinblick darauf, was man aus den Ergebnissen einer Studie schließen kann? In der öffentlichen Gesundheit und in der klinischen Forschung ist es die Standardpraxis, p ≤ 0,05 zu verwenden, um statistische Signifikanz anzuzeigen. Mit anderen Worten, jahrzehntelange Forscher auf diesem Gebiet haben gemeinsam entschieden, dass wir die Nullhypothese „verwerfen“, wenn die Chance, einen Fehler vom Typ I zu begehen (mehr dazu weiter unten), 5 % oder weniger beträgt. Wenn wir das Beispiel mit der Körpergröße von oben fortsetzen, würden wir also schlussfolgern, dass es einen Unterschied in der Körpergröße zwischen den Geschlechtern gibt, zumindest bei den Studenten im Grundstudium. Bei p-Werten über 0,05 „verwerfen wir die Nullhypothese nicht“ und schlussfolgern stattdessen, dass unsere Daten keinen Beweis dafür liefern, dass es einen Unterschied in der Körpergröße zwischen männlichen und weiblichen Studenten gibt.
Wenn p > 0,05, verwerfen wir die Nullhypothese nicht. Wir akzeptieren niemals die Nullhypothese, weil es sehr schwierig ist, die Abwesenheit von etwas zu beweisen. „Akzeptieren“ der Nullhypothese impliziert, dass wir bewiesen haben, dass es wirklich keinen Unterschied in der Körpergröße zwischen männlichen und weiblichen Studenten gibt, was nicht der Fall ist. Wenn p > 0,05 ist, bedeutet das lediglich, dass wir keine Beweise gegen die Nullhypothese gefunden haben – nicht, dass es diese Beweise nicht gibt. Wir könnten eine seltsame Stichprobe bekommen haben, wir könnten eine zu kleine Stichprobe gehabt haben, usw. Es gibt ein ganzes Feld der klinischen Forschung (vergleichende Wirksamkeitsforschungvi), das sich dem Nachweis widmet, dass eine Behandlung nicht besser oder schlechter ist als eine andere; die Methoden dieses Feldes sind komplex, und die erforderlichen Stichprobengrößen sind ziemlich groß. Für die meisten epidemiologischen Studien bleiben wir einfach dabei, nicht abzulehnen.
Ist der Grenzwert p ≤ 0,05 willkürlich? Auf jeden Fall. Das sollte man im Hinterkopf behalten, insbesondere bei p-Werten, die sehr nahe an diesem Cutoff liegen. Ist 0,49 wirklich so verschieden von 0,51? Wahrscheinlich nicht, aber sie befinden sich auf gegenüberliegenden Seiten dieser willkürlichen Linie. Die Größe eines p-Wertes hängt von drei Dingen ab: der Stichprobengröße, der Effektgröße (es ist einfacher, die Nullhypothese abzulehnen, wenn der wahre Unterschied in der Körpergröße – wenn wir jeden in der Population messen würden, anstatt nur unsere Stichprobe – 6 Zoll anstatt 2 Zoll beträgt) und der Konsistenz der Daten, die am häufigsten durch die Standardabweichungen um die mittlere Körpergröße in den beiden Gruppen gemessen wird. Daher könnte ein p-Wert von 0,51 mit ziemlicher Sicherheit kleiner gemacht werden, indem einfach mehr Personen in die Studie aufgenommen werden (dies bezieht sich auf die Aussagekraft, die das Gegenteil des Typ-II-Fehlers ist, der unten besprochen wird). Es ist wichtig, diese Tatsache im Hinterkopf zu behalten, wenn Sie Studien lesen.
Statistische Signifikanztests gehören zu einem Zweig der Statistik, der als frequentistische Statistik bezeichnet wird.ii Obwohl sie in der Epidemiologie und verwandten Bereichen sehr verbreitet sind, wird diese Praxis aus einer Reihe von Gründen nicht allgemein als ideale Wissenschaft angesehen. Zuallererst ist der Grenzwert von 0,05 völlig willkürlich,iii und ein strenger Signifikanztest würde die Null für p = 0,049 zurückweisen, aber nicht für p = 0,051, obwohl sie fast identisch sind. Zweitens gibt es viel mehr Nuancen bei der Interpretation von p-Werten und Konfidenzintervallen als die, die ich in diesem Kapitel behandelt habe.iv Zum Beispiel testet der p-Wert wirklich alle Analyseannahmen, nicht nur die Nullhypothese, und ein großer p-Wert zeigt oft nur an, dass die Daten nicht zwischen zahlreichen konkurrierenden Hypothesen unterscheiden können. Da jedoch sowohl das öffentliche Gesundheitswesen als auch die klinische Medizin Ja-oder-Nein-Entscheidungen erfordern (Sollen wir Ressourcen für diese Aufklärungskampagne aufwenden? Sollte dieser Patient dieses Medikament bekommen?), muss es ein System geben, um Ja oder Nein zu entscheiden, und das ist derzeit der statistische Signifikanztest. Es gibt andere Möglichkeiten, den Zufallsfehler zu quantifizieren, und in der Tat wird die Bayes’sche Statistik (die anstelle einer Ja-oder-Nein-Antwort eine Wahrscheinlichkeit dafür liefert, dass etwas passiert)ii immer beliebter. Da jedoch die frequentistische Statistik und der Nullhypothesentest immer noch die bei weitem am häufigsten verwendeten Methoden in der epidemiologischen Literatur sind, stehen sie im Mittelpunkt dieses Kapitels.
Typ-I- und Typ-II-Fehler
Ein Typ-I-Fehler (gewöhnlich symbolisiert durch α, den griechischen Buchstaben Alpha, und eng verwandt mit den p-Werten) ist die Wahrscheinlichkeit, dass Sie die Nullhypothese fälschlicherweise ablehnen – mit anderen Worten, dass Sie etwas „finden“, das nicht wirklich vorhanden ist. Indem wir 0,05 als statistische Signifikanzgrenze gewählt haben, haben wir in der öffentlichen Gesundheit und in der klinischen Forschung stillschweigend zugestimmt, dass wir bereit sind, zu akzeptieren, dass 5 % unserer Ergebnisse tatsächlich Typ-I-Fehler oder falsch-positive Ergebnisse sind.
Ein Typ-II-Fehler (gewöhnlich symbolisiert durch β, den griechischen Buchstaben Beta) ist das Gegenteil: β ist die Wahrscheinlichkeit, dass Sie die Nullhypothese fälschlicherweise nicht ablehnen – mit anderen Worten, dass Sie etwas übersehen, das wirklich vorhanden ist.
Die Power in epidemiologischen Studien variiert stark: Idealerweise sollte sie mindestens 90% betragen (was bedeutet, dass die Typ-II-Fehlerrate 10% beträgt), aber oft ist sie viel niedriger. Die Aussagekraft ist proportional zur Stichprobengröße, aber in exponentieller Weise – die Aussagekraft steigt mit zunehmender Stichprobengröße, aber um von 90 auf 95 % Aussagekraft zu kommen, ist ein viel größerer Sprung in der Stichprobengröße erforderlich als um von 40 auf 45 % Aussagekraft zu kommen. Wenn eine Studie die Nullhypothese nicht zurückweisen kann, aber die Daten so aussehen, als ob es einen großen Unterschied zwischen den Gruppen geben könnte, liegt das Problem oft darin, dass die Studie nicht ausreichend aussagekräftig war, und mit einer größeren Stichprobe würde der p-Wert wahrscheinlich unter den magischen Grenzwert von 0,05 fallen. Andererseits besteht ein Teil des Problems bei kleinen Stichproben darin, dass Sie vielleicht nur zufällig eine nicht repräsentative Stichprobe erhalten haben und das Hinzufügen zusätzlicher Teilnehmer die Ergebnisse nicht in Richtung statistischer Signifikanz treiben würde. Nehmen wir als Beispiel an, dass wir wieder an geschlechtsspezifischen Größenunterschieden interessiert sind, aber diesmal nur unter College-Sportlern. Wir beginnen mit einer sehr kleinen Studie – nur ein Männerteam und ein Frauenteam. Wenn wir z.B. die Basketballmannschaft der Männer und die Gymnastikmannschaft der Frauen auswählen, werden wir wahrscheinlich einen gewaltigen Unterschied in der durchschnittlichen Körpergröße finden – vielleicht 18 Zoll oder mehr. Das Hinzufügen anderer Teams zu unserer Studie würde mit ziemlicher Sicherheit zu einem viel geringeren Unterschied in der durchschnittlichen Körpergröße führen, und der in unserer anfänglichen kleinen Studie „gefundene“ Unterschied von 18 Zoll würde sich im Laufe der Zeit nicht halten.
Konfidenzintervalle
Da wir das akzeptable \alpha-Niveau auf 5 % festgelegt haben, verwenden wir in der Epidemiologie und verwandten Bereichen meistens 95 %-Konfidenzintervalle (95 % CI). Man kann ein 95%-KI verwenden, um Signifikanztests durchzuführen: Wenn das 95%-KI den Nullwert nicht einschließt (0 für die Risikodifferenz und 1,0 für Odds Ratios, Risk Ratios und Rate Ratios), dann ist p < 0.05, und das Ergebnis ist statistisch signifikant.
Obwohl 95% CI für Signifikanztests verwendet werden können, enthalten sie viel mehr Informationen als nur, ob der p-Wert <0,05 ist oder nicht. Die meisten epidemiologischen Studien geben 95%-KI um die dargestellten Punktschätzer herum an. Die korrekte Interpretation eines 95%-KI ist wie folgt:
Wir können dies auch visuell veranschaulichen:
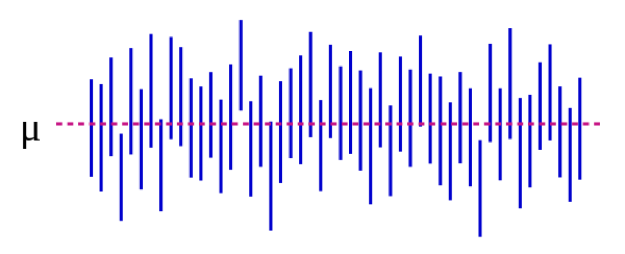
Quelle: https://es.wikipedia.org/wiki/Intervalo_de_confianza
In Abbildung 5-1 stellt der Populationsparameter μ die „echte“ Antwort dar, die man erhalten würde, wenn man absolut jeden in der Population in die Studie aufnehmen könnte. Wir schätzen μ mit Daten aus unserer Stichprobe. Um bei unserem Beispiel der Körpergröße zu bleiben: Wenn wir auf magische Weise die Körpergröße jedes einzelnen Studenten in den USA (oder auf der ganzen Welt, je nachdem, wie Sie Ihre Zielpopulation definieren) messen könnten, würde der mittlere Unterschied zwischen männlichen und weiblichen Studenten 5 Zoll betragen. Wichtig ist, dass dieser Populationsparameter fast immer unbeobachtbar ist – er wird nur beobachtbar, wenn Sie Ihre Population so eng definieren, dass Sie jeden einschließen können. Jede blaue vertikale Linie repräsentiert den CI einer einzelnen „Studie“ – in diesem Fall 50 Stück. Die CIs variieren, weil die Stichprobe jedes Mal etwas anders ist – die meisten CIs (alle bis auf 3) enthalten jedoch μ.
Wenn wir unsere Studie durchführen und einen mittleren Unterschied von 4 Zoll (95% CI, 1.5 – 7) finden, sagt uns der CI zwei Dinge. Erstens würde der p-Wert für unseren t-Test <0,05 sein, da der CI 0 ausschließt (der Nullwert in diesem Fall, da wir ein Differenzmaß berechnen). Zweitens ist die Interpretation des CI: Wenn wir unsere Studie 100 Mal wiederholen würden (einschließlich der Ziehung einer neuen Stichprobe), dann würde unser CI in 95 dieser Fälle den tatsächlichen Wert einschließen (von dem wir hier wissen, dass er 5 Zoll beträgt, den Sie aber im wirklichen Leben nicht kennen würden). Wenn man also den CI von 1,5 – 7,0 Zoll betrachtet, erhält man eine Vorstellung davon, wie groß der tatsächliche Unterschied sein könnte – er liegt mit ziemlicher Sicherheit irgendwo in diesem Bereich, könnte aber so klein wie 1,5 Zoll oder so groß wie 7 Zoll sein. Wie die p-Werte hängen auch die CIs vom Stichprobenumfang ab. Eine große Stichprobe ergibt einen vergleichsweise schmaleren CI. Engere CIs werden als besser angesehen, weil sie eine genauere Schätzung der „wahren“ Antwort liefern.
Zusammenfassung
Zufallsfehler sind bei allen Messungen vorhanden, obwohl einige Variablen anfälliger dafür sind als andere. P-Werte und CIs werden verwendet, um den Zufallsfehler zu quantifizieren. Ein p-Wert von 0,05 oder weniger wird normalerweise als „statistisch signifikant“ angesehen, und der entsprechende CI würde den Nullwert ausschließen. CIs sind nützlich, um den potenziellen Bereich des geschätzten „echten“ Wertes auf Bevölkerungsebene auszudrücken.
i. Butter in den USA und im Rest der Welt. Errens Kitchen. März 2014. https://www.errenskitchen.com/cooking-conversions/butter-measurement-weight-conversions/. Accessed September 26, 2018. (↵ Return)
ii. Bayesianischer vs. frequentistischer Ansatz: gleiche Daten, entgegengesetzte Ergebnisse. 365 Data Sci. August 2017. https://365datascience.com/bayesian-vs-frequentist-approach/. Accessed October 17, 2018. (↵ Return 1) (↵ Return 2)
iii. Smith RJ. The continuing misuse of null hypothesis significance testing in biological anthropology. Am J Phys Anthropol. 2018;166(1):236-245. doi:10.1002/ajpa.23399 (↵ Return)
iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. P-Values and reproductive health: what can clinical researchers learn from the American Statistical Association? Hum Reprod Oxf Engl. 2016;31(11):2406-2410. doi:10.1093/humrep/dew192 (↵ Return)
v. Greenland S, Senn SJ, Rothman KJ, et al. Statistische Tests, p-Werte, Konfidenzintervalle und Power: ein Leitfaden für Fehlinterpretationen. Eur J Epidemiol. 2016;31:337-350. doi:10.1007/s10654-016-0149-3
vi. Warum ist vergleichende Wirksamkeitsforschung wichtig? Patient-Centered Outcomes Research Institute. https://www.pcori.org/files/why-comparative-effectiveness-research-important. Accessed October 17, 2018. (↵ Return)
- Es gibt nicht nur eine Formel zur Berechnung eines p-Wertes oder eines CIs. Vielmehr ändern sich die Formeln je nachdem, welcher statistische Test angewendet wird. Jeder einführende Biostatistik-Text, der bespricht, welche statistischen Methoden wann anzuwenden sind, würde auch die entsprechenden Informationen zur p-Wert- und CI-Berechnung liefern. ↵
- Verbringen Sie nicht zu viel Zeit damit, herauszufinden, warum wir eine Nullhypothese brauchen; wir brauchen sie einfach. Die Begründung ist in Jahrhunderten akademischer wissenschaftsphilosophischer Argumente begraben. ↵
- Wie man den richtigen Test wählt, geht über den Rahmen dieses Buches hinaus – siehe jedes Buch über einführende Biostatistik ↵
Inhärent in allen Messungen. „Rauschen“ in den Daten. Wird immer vorhanden sein, aber die Menge hängt davon ab, wie genau Ihre Messinstrumente sind. Zum Beispiel haben Badezimmerwaagen normalerweise einen Zufallsfehler von 0,5 – 1 Pfund; in Physiklabors gibt es oft Waagen, die nur ein paar Mikrogramm Zufallsfehler haben (diese sind teurer und können nur kleine Mengen wiegen). Man kann den Einfluss des Zufallsfehlers auf die Studienergebnisse verringern, indem man den Stichprobenumfang erhöht. Dadurch wird der Zufallsfehler nicht eliminiert, sondern der Forscher kann die Daten innerhalb des Rauschens besser erkennen. Daraus folgt, dass eine Vergrößerung der Stichprobe den p-Wert verringert und das Konfidenzintervall verkleinert, da dies Möglichkeiten zur Quantifizierung des zufälligen Fehlers sind.
Systematischer Fehler. Selektionsverzerrungen entstehen durch eine schlechte Stichprobenziehung (Ihre Stichprobe ist nicht repräsentativ für die Zielpopulation), eine schlechte Rücklaufquote von denjenigen, die zur Teilnahme an einer Studie eingeladen wurden, durch die unterschiedliche Behandlung von Fällen und Kontrollen oder exponierten/unexponierten Personen und/oder durch ungleiche Verluste bis zum Follow-up zwischen den Gruppen. Um eine Selektionsverzerrung zu beurteilen, fragen Sie sich „wen haben sie erwischt und wen haben sie übersehen?“ – und dann fragen Sie sich auch „spielt das eine Rolle“? Manchmal spielt es eine Rolle, manchmal aber auch nicht.
Fehlklassifikationsbias bedeutet, dass etwas (entweder die Exposition, das Ergebnis, ein Confounder oder alle drei) falsch gemessen wurde. Beispiele sind, dass Menschen nicht in der Lage sind, Ihnen etwas zu sagen, dass Menschen nicht bereit sind, Ihnen etwas zu sagen, und dass eine objektive Messung irgendwie systematisch falsch ist (z.B. immer in die gleiche Richtung abweicht, wie eine Blutdruckmanschette, die nicht korrekt nullgestellt ist). Recall Bias, Social Desirability Bias, Interviewer Bias – das sind alles Beispiele für Misclassification Bias. Das Endergebnis ist, dass Personen in einer 2×2-Tabelle in das falsche Feld eingeordnet werden. Wenn die Fehlklassifikation gleichmäßig zwischen den Gruppen verteilt ist (z. B. haben sowohl exponierte als auch nicht exponierte Personen die gleiche Chance, in das falsche Feld gesetzt zu werden), handelt es sich um nicht-differentielle Fehlklassifikation. Andernfalls handelt es sich um eine differentielle Fehlklassifikation.
Eine Möglichkeit, den Zufallsfehler zu quantifizieren. Die korrekte Interpretation eines p-Wertes ist: die Wahrscheinlichkeit, dass man bei einer Wiederholung der Studie (zurück zur Zielpopulation gehen, eine neue Stichprobe ziehen, alles messen, die Analyse durchführen) ein Ergebnis finden würde, das mindestens so extrem ist, vorausgesetzt die Nullhypothese ist wahr. Wenn es tatsächlich wahr ist, dass es keinen Unterschied zwischen den Gruppen gibt, Ihre Studie aber herausgefunden hat, dass es 15% mehr Raucher in Gruppe A gibt, mit einem p-Wert von 0,06, dann bedeutet das, dass es eine 6%ige Chance gibt, dass Sie, wenn Sie die Studie wiederholen, wieder 15% (oder eine größere Zahl) mehr Raucher in einer der Gruppen finden würden. In der öffentlichen Gesundheit und in der klinischen Forschung verwenden wir normalerweise einen Grenzwert von p < 0,05, um „statistisch signifikant“ zu bedeuten – wir erlauben also eine Typ-I-Fehlerrate von 5%. In 5% der Fälle werden wir also etwas „finden“, obwohl es in Wirklichkeit keinen Unterschied gibt (d.h. obwohl die Nullhypothese wahr ist). In den anderen 95% der Fälle lehnen wir die Nullhypothese korrekt ab und folgern, dass es einen Unterschied zwischen den Gruppen gibt.
Eine Möglichkeit, den Zufallsfehler zu quantifizieren. Die korrekte Interpretation eines Konfidenzintervalls ist: Wenn Sie die Studie 100 Mal wiederholen (zurück zur Zielpopulation gehen, eine neue Stichprobe nehmen, alles messen, die Analyse durchführen), dann wird das Konfidenzintervall, das Sie als Teil dieses Prozesses berechnen, in 95 von 100 Fällen den wahren Wert enthalten, vorausgesetzt, die Studie enthält keine Verzerrung. Hier ist der wahre Wert derjenige, den Sie erhalten würden, wenn Sie in der Lage wären, jeden aus der Population in Ihre Studie einzuschließen – dies ist fast nie tatsächlich beobachtbar, da Populationen normalerweise zu groß sind, um jeden in eine Stichprobe einzuschließen. Korollarisch: Wenn Ihre Population klein genug ist, dass Sie jeden in Ihre Studie aufnehmen können, dann ist die Berechnung eines Konfidenzintervalls überflüssig.
Wird bei statistischen Signifikanztests verwendet. Die Nullhypothese ist immer, dass es keinen Unterschied zwischen den beiden untersuchten Gruppen gibt.
Ein statistischer Test, der bestimmt, ob die Mittelwerte in zwei Gruppen unterschiedlich sind.
Eine etwas willkürliche Methode, um zu bestimmen, ob man den Ergebnissen einer Studie Glauben schenken soll oder nicht. In der klinischen und epidemiologischen Forschung wird die statistische Signifikanz typischerweise auf p < 0,05 festgelegt, was eine Fehlerrate vom Typ I von <5% bedeutet. Wie bei allen statistischen Methoden gilt auch hier, dass es sich nur um einen zufälligen Fehler handelt; eine Studie kann statistisch signifikant sein, aber nicht glaubwürdig, z.B. wenn die Wahrscheinlichkeit einer erheblichen Verzerrung besteht. Eine Studie kann auch statistisch signifikant sein (z.B. p war < 0,05), aber klinisch nicht signifikant (z.B. wenn der Unterschied im systolischen Blutdruck zwischen den beiden Gruppen 2 mm Hg betrug – bei einer ausreichend großen Stichprobe wäre dies statistisch signifikant, aber es ist klinisch überhaupt nicht von Bedeutung).
Die Wahrscheinlichkeit, dass eine Studie etwas „findet“, das nicht vorhanden ist. Wird typischerweise durch α dargestellt und ist eng mit den p-Werten verwandt. Wird für klinische und epidemiologische Studien üblicherweise auf 0,05 gesetzt.
Die Wahrscheinlichkeit, dass Ihre Studie etwas findet, das da ist. Power = 1 – β; beta ist die Fehlerrate vom Typ II. Kleine Studien oder Studien zu seltenen Ereignissen haben typischerweise eine zu geringe Power.
Die Wahrscheinlichkeit, dass eine Studie etwas nicht gefunden hat, das da war. Wird typischerweise durch β dargestellt und hängt eng mit der Power zusammen. Im Idealfall liegt sie bei klinischen und epidemiologischen Studien über 90 %, obwohl dies in der Praxis oft nicht der Fall ist.
Das Maß der Assoziation, das in einer Studie berechnet wird. Wird typischerweise mit einem entsprechenden 95%-Konfidenzintervall angegeben.