Die Heaviside-Schrittfunktion ist eine mathematische Funktion mit der Bezeichnung 
, oder manchmal 
oder 
(Abramowitz und Stegun 1972, S. 1020), und auch als „Einheitsschrittfunktion“ bekannt. Der Begriff „Heaviside-Stufenfunktion“ und ihr Symbol können entweder eine stückweise konstante Funktion oder eine verallgemeinerte Funktion darstellen.
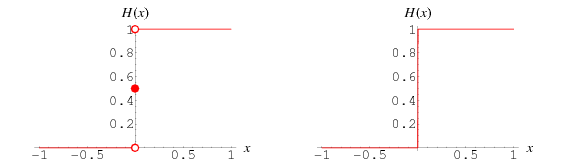
Wenn sie als stückweise konstante Funktion definiert ist, ist die Heaviside-Stufenfunktion gegeben durch
 |
(1)
|
(Abramowitz und Stegun 1972, p. 1020; Bracewell 2000, S. 61). Das obige Diagramm zeigt diese Funktion (linke Abbildung) und wie sie bei der Darstellung auf einem Oszilloskop aussehen würde (rechte Abbildung).
Wenn sie als verallgemeinerte Funktion definiert ist, kann sie als eine Funktion 
definiert werden, die
 |
(2)
|
für 
die Ableitung einer hinreichend glatten Funktion 
, die hinreichend schnell abklingt (Kanwal 1998).
Die Wolfram Language stellt die verallgemeinerte Heaviside-Funktion als HeavisideTheta dar, während sie die stückweise Funktion Piecewise mit UnitStep repräsentiert (die, wohlgemerkt, die Konvention 
anstelle der konventionellen Definition 
übernimmt).
Die Kurzschreibweise
 |
(3)
|
wird manchmal auch verwendet.
Die Heaviside-Stufenfunktion ist mit der Boxcarfunktion verwandt durch
 |
(4)
|
und kann in Bezug auf die Vorzeichenfunktion definiert werden durch
 |
(5)
|
Die Ableitung der der Stufenfunktion ist gegeben durch
 |
(6)
|
wobei 
die Delta-Funktion ist (Bracewell 2000, S. 97).
Die Heaviside-Stufenfunktion ist mit der Rampenfunktion 
verwandt durch
 |
(7)
|
und zur Ableitung von 
durch
 |
(8)
|
Die beiden sind auch verbunden durch
 |
(9)
|
wobei 
die Faltung bezeichnet.
Bracewell (2000) gibt viele Identitäten an, von denen einige die folgende sind. Lassen wir 
die Faltung bezeichnen,
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
Zudem,
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
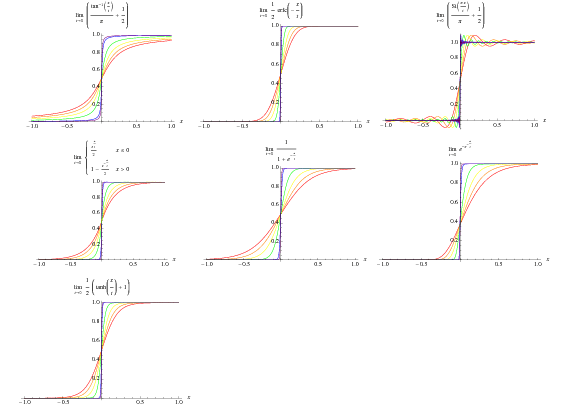
Die Heaviside-Stufenfunktion kann durch die folgenden Grenzwerte definiert werden,
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
 |
 |
 |
(21)
|
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
 |
 |
 |
(25)
|
 |
 |
 |
(26)
|
 |
 |
 |
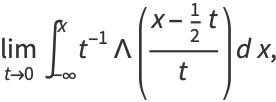(27)
|
wobei 
die erfc-Funktion ist, 
ist das Sinus-Integral, 
ist die sinc-Funktion und 
ist die Ein-Argument-Dreieck-Funktion. Die ersten vier davon sind oben für 
, 0,1 und 0,01 dargestellt.
Natürlich ist jede monotone Funktion mit konstanten ungleichen horizontalen Asymptoten eine Heaviside-Stufenfunktion unter geeigneter Skalierung und möglicher Spiegelung. Die Fourier-Transformierte der Heaviside-Stufenfunktion ist gegeben durch
 |
 |
 |
(28)
|
 |
 |
 |
(29)
|
wobei 
die Deltafunktion ist.