Eine 
Matrix 
ist eine orthogonale Matrix, wenn
 |
(1)
|
wobei 
die Transponierte von 
ist und 
die Identitätsmatrix ist. Insbesondere ist eine orthogonale Matrix immer invertierbar, und
 |
(2)
|
In Komponentenform,
 |
(3)
|
Durch diese Beziehung sind orthogonale Matrizen besonders einfach zu berechnen, da die Transponierungsoperation viel einfacher ist als die Berechnung einer Inversen.
Beispielsweise,
 |
 |
 |
(4)
|
 |
 |
 |
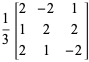(5)
|
Sind orthogonale Matrizen.
Eine Matrix 
kann in der Wolfram Language mit OrthogonalMatrixQ auf ihre Orthogonalität getestet werden.
Die Zeilen einer orthogonalen Matrix bilden eine Orthonormalbasis. Das heißt, jede Zeile hat die Länge eins und ist zueinander senkrecht. In ähnlicher Weise sind auch die Spalten eine orthonormale Basis. Tatsächlich ist bei jeder orthonormalen Basis die Matrix, deren Zeilen diese Basis sind, eine orthogonale Matrix. Es ist automatisch der Fall, dass die Spalten eine weitere orthonormale Basis sind.
Die orthogonalen Matrizen sind genau die Matrizen, die das Innenprodukt erhalten
 |
(6)
|
Also, ist die Determinante von 
entweder 1 oder 
. Als Teilmenge von 
sind die orthogonalen Matrizen nicht verbunden, da die Determinante eine stetige Funktion ist. Stattdessen gibt es zwei Komponenten, je nachdem, ob die Determinante 1 oder 
ist. Die orthogonalen Matrizen mit 
sind Rotationen, und eine solche Matrix heißt eine spezielle orthogonale Matrix.
Das Matrixprodukt zweier orthogonaler Matrizen ist eine weitere orthogonale Matrix. Außerdem ist die Inverse einer orthogonalen Matrix eine orthogonale Matrix, ebenso wie die Identitätsmatrix. Daher bildet die Menge der orthogonalen Matrizen eine Gruppe, die orthogonale Gruppe 
.