![]()
Eine Vektorbasis eines Vektorraums ![]() ist definiert als eine Teilmenge
ist definiert als eine Teilmenge ![]() von Vektoren in
von Vektoren in ![]() , die linear unabhängig sind und
, die linear unabhängig sind und ![]() aufspannen. Folglich, wenn
aufspannen. Folglich, wenn ![]() eine Liste von Vektoren in
eine Liste von Vektoren in ![]() ist, dann bilden diese Vektoren eine Vektorbasis, wenn und nur wenn jedes
ist, dann bilden diese Vektoren eine Vektorbasis, wenn und nur wenn jedes ![]() eindeutig geschrieben werden kann als
eindeutig geschrieben werden kann als
|
(1)
|
wobei ![]()
![]() sind Elemente des Basisfeldes.
sind Elemente des Basisfeldes.
Wenn das Basisfeld die Reellen sind, so dass ![]() für
für ![]() , sind die resultierenden Basisvektoren
, sind die resultierenden Basisvektoren ![]() -Tupel von Realen, die den
-Tupel von Realen, die den ![]() -dimensionalen euklidischen Raum
-dimensionalen euklidischen Raum ![]() aufspannen. Andere mögliche Basisfelder sind die Komplexe
aufspannen. Andere mögliche Basisfelder sind die Komplexe ![]() , sowie verschiedene Felder positiver Charakteristik, die in der Algebra, Zahlentheorie und algebraischen Geometrie betrachtet werden.
, sowie verschiedene Felder positiver Charakteristik, die in der Algebra, Zahlentheorie und algebraischen Geometrie betrachtet werden.
Ein Vektorraum ![]() hat viele verschiedene Vektorbasen, aber es gibt immer die gleiche Anzahl von Basisvektoren in jeder von ihnen. Die Anzahl der Basisvektoren in
hat viele verschiedene Vektorbasen, aber es gibt immer die gleiche Anzahl von Basisvektoren in jeder von ihnen. Die Anzahl der Basisvektoren in ![]() wird die Dimension von
wird die Dimension von ![]() genannt. Jede aufspannende Liste in einem Vektorraum kann auf eine Basis des Vektorraums reduziert werden.
genannt. Jede aufspannende Liste in einem Vektorraum kann auf eine Basis des Vektorraums reduziert werden.
Das einfachste Beispiel für eine Vektorbasis ist die Standardbasis im euklidischen Raum ![]() , in dem die Basisvektoren entlang jeder Koordinatenachse liegen. Mit einem Basiswechsel können Vektoren (und Operatoren) in einer gegebenen Basis in eine andere transformiert werden.
, in dem die Basisvektoren entlang jeder Koordinatenachse liegen. Mit einem Basiswechsel können Vektoren (und Operatoren) in einer gegebenen Basis in eine andere transformiert werden.
Gegeben eine Hyperebene, die definiert ist durch
|
(2)
|
eine Basis kann gefunden werden, indem man ![]() in Termen von
in Termen von ![]() löst,
löst, ![]()
![]() , und
, und ![]() . Die Durchführung dieses Verfahrens,
. Die Durchführung dieses Verfahrens,
|
(3)
|
so
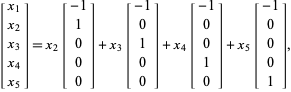 |
(4)
|
Und die obigen Vektoren bilden eine (nicht normierte) Basis.
Gegeben eine Matrix ![]() mit einer orthonormalen Basis, so ist die Matrix, die einer Änderung der Basis entspricht, ausgedrückt in Form der ursprünglichen
mit einer orthonormalen Basis, so ist die Matrix, die einer Änderung der Basis entspricht, ausgedrückt in Form der ursprünglichen ![]() ist
ist
|
(5)
|
Wenn ein Vektorraum unendlich dimensional ist, dann existiert eine Basis, solange man das Wahlaxiom annimmt. Eine Teilmenge der Basis, die linear unabhängig ist und deren Spannweite dicht ist, heißt vollständige Menge und ist ähnlich wie eine Basis. Wenn ![]() ein Hilbert-Raum ist, dann heißt eine vollständige Menge Hilbert-Basis.
ein Hilbert-Raum ist, dann heißt eine vollständige Menge Hilbert-Basis.