Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Expliquer un scénario dans lequel les champs magnétiques et électriques sont croisés et leurs forces s’équilibrent lorsqu’une particule chargée se déplace à travers un sélecteur de vitesse
- Comparer comment les porteurs de charge se déplacent dans un matériau conducteur et expliquer comment cela est lié à l’effet Hall
En 1879, E.H. Hall a conçu une expérience qui peut être utilisée pour identifier le signe des porteurs de charge prédominants dans un matériau conducteur. D’un point de vue historique, cette expérience a été la première à démontrer que les porteurs de charge dans la plupart des métaux sont négatifs.
Visitez ce site web pour trouver plus d’informations sur l’effet Hall.
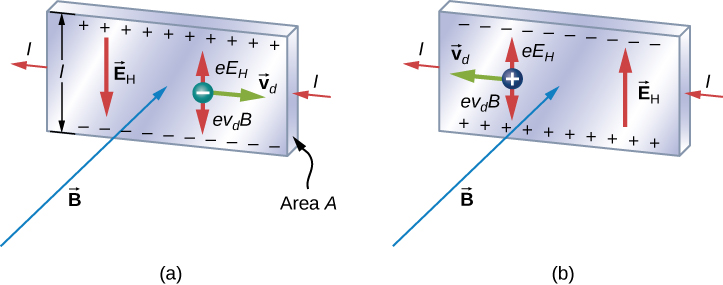
Nous étudions l’effet Hall en étudiant le mouvement des électrons libres le long d’une bande métallique de largeur l dans un champ magnétique constant (figure \(\PageIndex{1}\)). Les électrons se déplaçant de gauche à droite, la force magnétique qu’ils subissent les pousse vers le bord inférieur de la bande. Cela laisse un excès de charge positive sur le bord supérieur de la bande, ce qui crée un champ électrique E dirigé du haut vers le bas. La concentration de charges aux deux bords s’accumule jusqu’à ce que la force électrique sur les électrons dans une direction soit équilibrée par la force magnétique sur eux dans la direction opposée. L’équilibre est atteint lorsque :
\
où e est la magnitude de la charge de l’électron, \(v_d\) est la vitesse de dérive des électrons, et E est la magnitude du champ électrique créé par la charge séparée. En résolvant ceci pour la vitesse de dérive, on obtient
Un scénario dans lequel les champs électriques et magnétiques sont perpendiculaires les uns aux autres est appelé une situation de champ croisé. Si ces champs produisent des forces égales et opposées sur une particule chargée avec la vitesse qui égalise les forces, ces particules sont capables de passer à travers un appareil, appelé sélecteur de vitesse, sans être déviées. Cette vitesse est représentée dans l’équation \ref{11.26}. Toute autre vitesse d’une particule chargée envoyée dans les mêmes champs serait déviée par la force magnétique ou la force électrique.
Pour en revenir à l’effet Hall, si le courant dans la bande est I, alors à partir de Courant et résistance, nous savons que
\
où n est le nombre de porteurs de charge par volume et A est la surface de la section transversale de la bande. En combinant les équations pour \(v_d\) et I, on obtient
Le champ E est lié à la différence de potentiel V entre les bords de la bande par
La quantité \(V\) est appelée le potentiel de Hall et peut être mesurée avec un voltmètre. Enfin, en combinant les équations pour I et E, on obtient
où le bord supérieur de la bande de la figure \(\PageIndex{1}\) est positif par rapport au bord inférieur.
On peut également combiner l’équation \ref{11.24} et l’équation \ref{11.28} pour obtenir une expression de la tension de Hall en fonction du champ magnétique :
Qu’en est-il si les porteurs de charge sont positifs, comme sur la figure \(\PageIndex{1}\) ? Pour le même courant I, la magnitude de V est toujours donnée par l’équation \ref{hallV}. Cependant, le bord supérieur est maintenant négatif par rapport au bord inférieur. Par conséquent, en mesurant simplement le signe de V, nous pouvons déterminer le signe des porteurs de charge majoritaires dans un métal.
Les mesures du potentiel de Hall montrent que les électrons sont les porteurs de charge dominants dans la plupart des métaux. Cependant, les potentiels de Hall indiquent que pour quelques métaux, comme le tungstène, le béryllium et de nombreux semi-conducteurs, la majorité des porteurs de charge sont positifs. Il s’avère que la conduction par charge positive est causée par la migration des sites d’électrons manquants (appelés trous) sur les ions. La conduction par les trous est étudiée plus loin dans la physique de la matière condensée.
L’effet Hall peut être utilisé pour mesurer les champs magnétiques. Si un matériau avec une densité connue de porteurs de charge n est placé dans un champ magnétique et que V est mesuré, alors le champ peut être déterminé à partir de l’équation \ref{11.29}. Dans les laboratoires de recherche où les champs des électro-aimants utilisés pour des mesures précises doivent être extrêmement stables, une » sonde de Hall » est couramment utilisée dans le cadre d’un circuit électronique qui régule le champ.
Exemple \(\PageIndex{1}\) : Sélecteur de vitesse
Un faisceau d’électrons entre dans un sélecteur de vitesse à champ croisé avec des champs magnétique et électrique de 2,0 mT et \(6,0 \times 10^3 \, N/C\), respectivement. (a) Quelle doit être la vitesse du faisceau d’électrons pour traverser les champs croisés sans être dévié ? Si le champ électrique est désactivé, (b) quelle est l’accélération du faisceau d’électrons et (c) quel est le rayon du mouvement circulaire qui en résulte ?
Stratégie
Le faisceau d’électrons n’est dévié par aucun des champs magnétique ou électrique si ces forces sont équilibrées. En fonction de ces forces équilibrées, on calcule la vitesse du faisceau. Sans le champ électrique, seule la force magnétique est utilisée dans la deuxième loi de Newton pour trouver l’accélération. Enfin, le rayon de la trajectoire est basé sur le mouvement circulaire résultant de la force magnétique.
Solution
- La vitesse du faisceau non perturbé d’électrons à champs croisés est calculée par l’équation \ref{11.25} : \
- L’accélération est calculée à partir de la force nette du champ magnétique, égale à la masse fois l’accélération. La magnitude de l’accélération est : \N
- Le rayon de la trajectoire provient de l’équilibre des forces circulaire et magnétique, soit l’équation \ref{11.25} : \
Signification
Si les électrons du faisceau avaient des vitesses supérieures ou inférieures à la réponse de la partie (a), ces électrons auraient une force nette plus forte exercée par le champ magnétique ou électrique. Par conséquent, seuls les électrons à cette vitesse spécifique passeraient à travers.
Le potentiel de Hall dans un ruban d’argent
La figure \(\PageIndex{2}\) montre un ruban d’argent dont la section transversale est de 1,0 cm par 0,20 cm. Le ruban transporte un courant de 100 A de gauche à droite, et il se trouve dans un champ magnétique uniforme de magnitude 1,5 T. En utilisant une valeur de densité de \(n = 5,9 \times 10^{28}\) électrons par mètre cube pour l’argent, trouver le potentiel de Hall entre les bords du ruban.
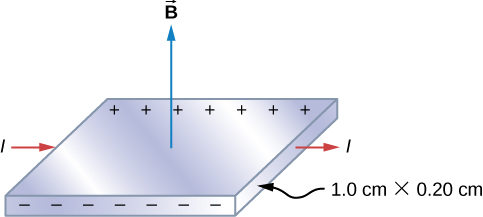
Stratégie
Puisque la majorité des porteurs de charge sont des électrons, la polarité de la tension de Hall est celle indiquée sur la figure. La valeur de la tension de Hall est calculée à l’aide de l’équation \ref{hallV}.
Solution
Lorsque l’on calcule la tension de Hall, il faut connaître le courant qui traverse le matériau, le champ magnétique, la longueur, le nombre de porteurs de charge et la surface. Comme tous ces éléments sont donnés, la tension de Hall se calcule comme suit :
\ &= \frac{(100 \, A)(1.5 \, T)(1.0 \times 10^{-2}m)}{(5.9 \times 10^{28} /m^3)(1.6 \times 10^{-19}C)(2.0 \times 10^{-5}m^2)} \\N &= 7.9 \times 10^{-6}V. \end{align*} \]
Signification
Comme dans cet exemple, le potentiel de Hall est généralement très faible, et une expérimentation minutieuse avec un équipement sensible est nécessaire pour sa mesure.
Exercice \(\PageIndex{1}\)
Une sonde de Hall est constituée d’une bande de cuivre, \(n = 8,5 \times 10^{28}\) électrons par mètre cube, qui mesure 2,0 cm de large et 0,10 cm d’épaisseur. Quel est le champ magnétique lorsque I = 50 A et que le potentiel de Hall est
- \(4,0 \, \mu V\) et
- \(6,0 \, \mu V\)?
Réponse a
1,1 T
Réponse b
1.6 T
Contributeurs et attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) et Bill Moebs avec de nombreux auteurs collaborateurs. Ce travail est autorisé par OpenStax University Physics sous une licence Creative Commons Attribution License (by 4.0).
.