Bases du graphique. Fonctions exponentielles
La fonction exponentielle y=b^x où b>0 est une fonction qui restera proportionnelle à sa valeur initiale lorsqu’elle croît ou décroît.
Objectifs d’apprentissage
Décrire les propriétés des graphiques des fonctions exponentielles
Principaux points à retenir
Principaux points
- Si la base, b, est supérieure à 1, alors la fonction augmente exponentiellement à un taux de croissance de b. C’est ce qu’on appelle la croissance exponentielle.
- Si la base, b, est inférieure à 1 (mais supérieure à 0), la fonction décroît exponentiellement à un taux de b. C’est ce qu’on appelle la décroissance exponentielle.
- Si la base, b, est égale à 1, alors la fonction devient trivialement y=a.
- Les points (0,1) et (1,b) sont toujours sur le graphe de la fonction y=b^x
- La fonction y=b^x ne prend que des valeurs positives et a pour asymptote horizontale l’axe des x.
Termes clés
- La croissance exponentielle : La croissance de la valeur d’une quantité, dans laquelle le taux de croissance est proportionnel à la valeur instantanée de la quantité ; par exemple, lorsque la valeur a doublé, le taux d’augmentation aura également doublé. Le taux peut être positif ou négatif. S’il est négatif, on parle aussi de décroissance exponentielle.
- asymptote : Une ligne dont une courbe s’approche arbitrairement de près. Une asymptote peut être verticale, oblique ou horizontale. Les asymptotes horizontales correspondent à la valeur dont la courbe s’approche lorsque x devient très grand ou très petit.
- Fonction exponentielle : Toute fonction dans laquelle une variable indépendante se présente sous la forme d’un exposant ; ce sont les fonctions inverses des logarithmes.
Définitions
Au niveau le plus élémentaire, une fonction exponentielle est une fonction dans laquelle la variable apparaît dans l’exposant. La fonction exponentielle la plus basique est une fonction de la forme y=b^x où b est un nombre positif.
Lorsque b>1 la fonction croît de manière proportionnelle à sa valeur initiale. On parle de croissance exponentielle.
Lorsque 0>b>1 la fonction décroît de manière proportionnelle à sa valeur initiale. C’est ce qu’on appelle la décroissance exponentielle.
Graphie d’une fonction exponentielle
considérons la fonction y=2^x lorsque b>1. Une façon de représenter graphiquement cette fonction est de choisir des valeurs pour x et de les substituer dans l’équation pour générer des valeurs pour y. Ce faisant, nous pouvons obtenir les points suivants :
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) et (2,4)
En reliant les points, vous remarquerez une courbe lisse qui croise l’axe des y au point (0,1) et qui augmente à mesure que x prend des valeurs de plus en plus grandes. Autrement dit, la courbe s’approche de l’infini lorsque x s’approche de l’infini. Au fur et à mesure que x prend des valeurs de plus en plus petites, la courbe se rapproche de plus en plus de l’axe des x. Autrement dit, la courbe s’approche de zéro lorsque x s’approche de l’infini négatif, ce qui fait que l’axe des x est une asymptote horizontale de la fonction. Le point (1,b) se trouve sur le graphique. Ceci est vrai du graphique de toutes les fonctions exponentielles de la forme y=b^x pour x>1.
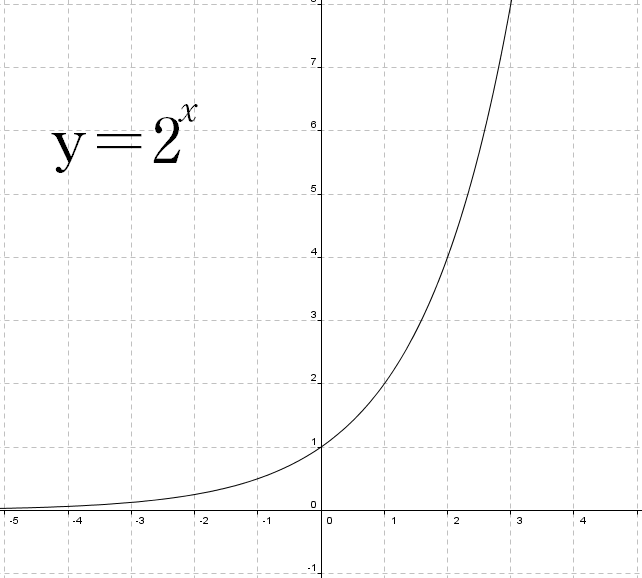
Graphe de y=2^x : Le graphique de cette fonction croise l’axe des y à (0,1) et augmente lorsque x s’approche de l’infini. L’axe des x est une asymptote horizontale de la fonction.
Exemple 2
Regardons la fonction y=\frac{1}{2}^x lorsque 0<b<1. Une façon de représenter graphiquement cette fonction est de choisir des valeurs pour x et de les substituer dans l’équation pour générer des valeurs pour y. En procédant ainsi, vous pouvez obtenir les points suivants :
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) et (2,\frac{1}{4})
En reliant les points, vous remarquerez une courbe lisse qui croise l’axe des y au point (0,1) et qui diminue à mesure que x prend des valeurs de plus en plus grandes. La courbe s’approche de l’infini zéro en s’approchant de l’infini. Au fur et à mesure que x prend des valeurs de plus en plus petites, la courbe se rapproche de plus en plus de l’axe des x. Autrement dit, la courbe s’approche de zéro lorsque x s’approche de l’infini négatif, faisant de l’axe des x une asymptote horizontale de la fonction. Le point (1,b) se trouve sur le graphique. Ceci est vrai du graphique de toutes les fonctions exponentielles de la forme y=b^x pour 0<x<1.
Comme vous pouvez le voir sur le graphique ci-dessous, le graphique de y=\frac{1}{2}^x est symétrique à celui de y=2^x sur l’axe des y. C’est-à-dire que si le plan était replié sur l’axe des y, les deux courbes seraient l’une sur l’autre.
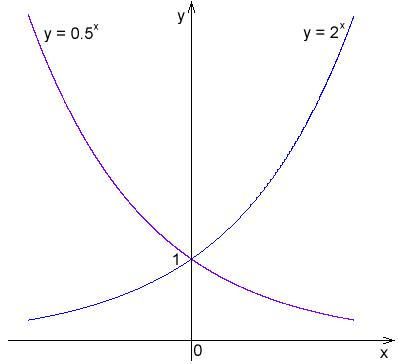
Graphe de y=2^x et y=\frac{1}{2}^x : Les graphes de ces fonctions sont symétriques sur l’axe des y.
Pourquoi b doit-il être un nombre positif ?
Si b=1, alors la fonction devient y=1^x. Comme 1 à toute puissance donne 1, la fonction est équivalente à y=1 qui est une ligne horizontale, et non une équation exponentielle.
Si b est négatif, alors élever b à une puissance paire entraîne une valeur positive pour y tandis qu’élever b à une puissance impaire entraîne une valeur négative pour y, ce qui rend impossible de joindre les points obtenus d’une manière significative et certainement pas d’une manière qui génère une courbe comme celles des exemples ci-dessus.
Propriétés des graphiques exponentiels
Le point (0,1) est toujours sur le graphique d’une fonction exponentielle de la forme y=b^x car b est positif et tout nombre positif à la puissance zéro donne 1.
Le point (1,b) est toujours sur le graphique d’une fonction exponentielle de la forme y=b^x car tout nombre positif b élevé à la première puissance donne 1.
La fonction y=b^x ne prend que des valeurs positives car tout nombre positif b ne donne que des valeurs positives lorsqu’il est élevé à une puissance quelconque.
La fonction y=b^x a pour asymptote horizontale l’axe des x car la courbe s’approchera toujours de l’axe des x lorsque x s’approche de l’infini positif ou négatif, mais ne traversera jamais l’axe car elle ne sera jamais égale à zéro.
Graphes des fonctions logarithmiques
Les fonctions logarithmiques peuvent être graphiées manuellement ou électroniquement, les points étant généralement déterminés via une calculatrice ou un tableau.
Objectifs d’apprentissage
Décrire les propriétés des graphiques des fonctions logarithmiques
Principaux points à retenir
Principaux points
- Lorsqu’elle est représentée graphiquement, la fonction logarithmique a une forme similaire à la fonction racine carrée, mais avec une asymptote verticale lorsque x s’approche de 0 par la droite.
- Le point (1,0) est sur le graphique de toutes les fonctions logarithmiques de la forme y=log{_b}x, où b est un nombre réel positif.
- Le domaine de la fonction logarithmique y=log{_b}x, où b est tout nombre réel positif, est l’ensemble de tous les nombres réels positifs, alors que l’étendue de cette fonction est tout nombre réel.
- Le graphique d’une fonction logarithmique de la forme y=log{_b}x peut être décalé horizontalement et/ou verticalement en ajoutant une constante à la variable x ou à y, respectivement.
- Une fonction logarithmique de la forme y=log{_b}x où b est un nombre réel positif, peut être représentée graphiquement en utilisant une calculatrice pour déterminer les points sur le graphique ou peut être représentée graphiquement sans calculatrice en utilisant le fait que son inverse est une fonction exponentielle.
Termes clés
- Fonction logarithmique : Toute fonction dans laquelle une variable indépendante apparaît sous la forme d’un logarithme. L’inverse d’une fonction logarithmique est une fonction exponentielle et vice versa.
- logarithme : Le logarithme d’un nombre est l’exposant par lequel une autre valeur fixe, la base, doit être élevée pour produire ce nombre.
- asymptote : Une ligne dont une courbe s’approche arbitrairement de près. Les asymptotes peuvent être horizontales, verticales ou obliques.
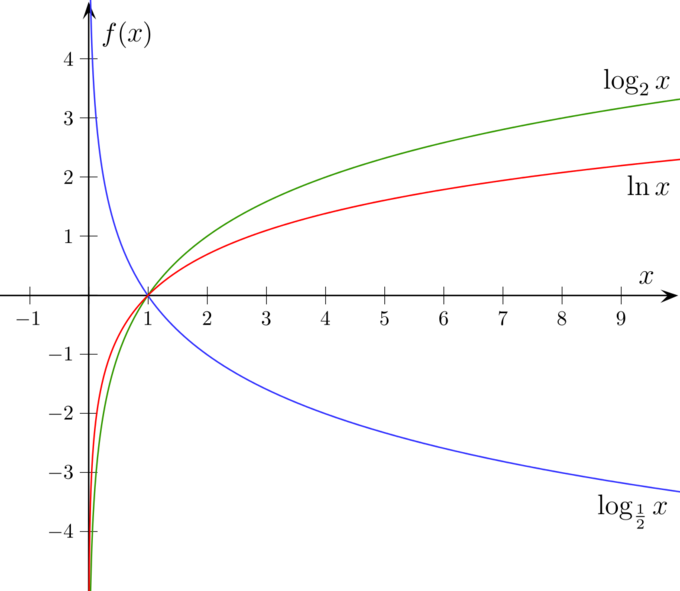
Vous trouverez ci-dessous des graphiques de fonctions logarithmiques avec les bases 2, e et 10.
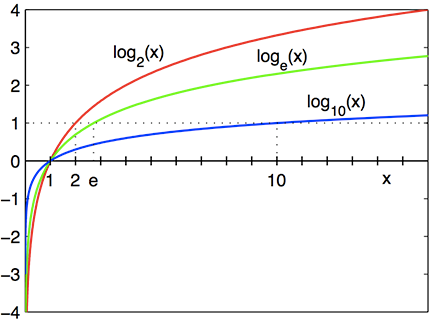
Graphes logarithmiques : Après x=1, là où les graphiques croisent l’axe des x, \log_2(x) en rouge est au-dessus de \log_e(x) en vert, qui est au-dessus de \log_{10}(x) en bleu. Avant ce point, l’ordre est inversé. Les trois logarithmes ont tous l’axe des y comme asymptote verticale, et sont toujours croissants.
Les trois graphiques logarithmiques commencent par une montée abrupte après x=0, mais s’étirent de plus en plus horizontalement, leur pente diminuant toujours au fur et à mesure que x augmente. Ils croisent tous l’axe des x à x=1.
Propriétés des graphes des fonctions logarithmiques
Le graphe croise l’axe des x à 1. Autrement dit, le graphe a une ordonnée à l’origine de 1 et, à ce titre, le point (1,0) se trouve sur le graphe. En fait, le point (1,0) sera toujours sur le graphique d’une fonction de la forme y=log{_b}x où b>0. En effet, pour x=1, l’équation du graphique devient y=log{_b}1.
On cherche donc un exposant y tel que b^y=1. Comme b>0, l’exposant que nous cherchons est 1 quelle que soit la valeur de b. Cela signifie que le point (x,y)=(1,0) sera toujours sur une fonction logarithmique de ce type.
Asymptotes
L’axe des y est une asymptote verticale du graphique. Cela signifie que la courbe se rapproche de plus en plus de l’axe des y mais ne le traverse pas.
Envisageons ce qui se passe lorsque la valeur de x s’approche de zéro par la droite pour l’équation dont le graphique apparaît ci-dessus. À savoir, y=log{_b}x. Pour ce faire, nous pouvons choisir des valeurs pour x, les brancher dans l’équation et générer des valeurs pour y.
Supposons que b est un nombre positif supérieur à 1, et étudions les valeurs de x entre 0 et 1. Dans ces conditions, si nous laissons x=\frac{1}{b}, l’équation devient y=log\frac{1}{b}.
Donc, nous cherchons un exposant tel que b élevé à cet exposant donne \frac{1}{b}. L’exposant que nous cherchons est -1 et le point (\frac{1}{b},-1) est sur le graphique. De même, nous pouvons obtenir les points suivants qui sont également sur le graphique :
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) et ainsi de suite
Si nous prenons des valeurs de x encore plus proches de 0, nous pouvons arriver aux points suivants : (\frac{1}{b^{10}},-10),(\frac{1}{b^{100}},-100) et (\frac{1}{b^{1000}},-1000)
Comme on peut le voir, plus la valeur de x se rapproche de 0, plus le graphique devient négatif. Autrement dit, lorsque x s’approche de zéro, le graphique se rapproche de l’infini négatif. Cela signifie que l’axe des y est une asymptote verticale de la fonction.
Domaine et étendue
Le domaine de la fonction est constitué de tous les nombres positifs. Cela signifie que la valeur x de la fonction sera toujours positive. Commençons par examiner pourquoi la valeur x de la courbe n’est jamais 0.
Si la valeur x était nulle, la fonction se lirait y=log{_b}0.
Ici, nous cherchons un exposant tel que b élevé à cet exposant soit 0. Comme b est un nombre positif, il n’existe pas d’exposant auquel on puisse élever b de façon à obtenir 0. En fait, comme b est positif, l’élever à une puissance donnera toujours un nombre positif.
L’étendue de la fonction est l’ensemble des nombres réels. Autrement dit, le graphique peut prendre n’importe quel nombre réel.
Comparaison entre y=log{_x} et y=\sqrt{x}
A première vue, le graphique de la fonction logarithmique peut facilement être confondu avec celui de la fonction racine carrée.
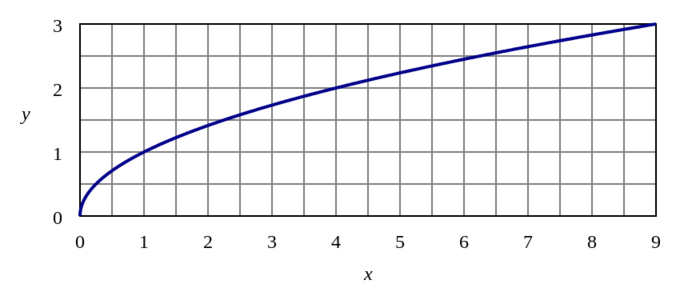
Graphe de y=\sqrt{x} : Le graphique de la fonction racine carrée ressemble à celui de la fonction logarithmique, mais ne possède pas d’asymptote verticale.
Les fonctions racine carrée et logarithmique ont toutes deux un domaine limité aux valeurs de x supérieures à 0. Cependant, la fonction logarithmique possède une asymptote verticale descendant vers -\infty lorsque x s’approche de 0, alors que la racine carrée atteint une valeur minimale de y de 0. Le domaine de la fonction racine carrée est constitué de tous les nombres réels non négatifs, alors que le domaine de la fonction logarithmique est constitué de tous les nombres réels.
Graphie des fonctions logarithmiques
La graphie des fonctions logarithmiques peut se faire en repérant des points sur la courbe soit manuellement, soit à l’aide d’une calculatrice.
Lorsque l’on graphie sans calculatrice, on utilise le fait que l’inverse d’une fonction logarithmique est une fonction exponentielle.
Lorsque nous faisons un graphique avec une calculatrice, nous utilisons le fait que la calculatrice ne peut calculer que des logarithmes communs (la base est 10), des logarithmes naturels (la base est e) ou des logarithmes binaires (la base est 2). Bien sûr, si nous avons une calculatrice graphique, la calculatrice peut tracer le graphique de la fonction sans que nous ayons besoin de trouver des points sur le graphique.
Tracer les fonctions logarithmiques en utilisant leurs inverses
Les fonctions logarithmiques peuvent être tracées à la main sans l’aide d’une calculatrice si nous utilisons le fait qu’elles sont les inverses des fonctions exponentielles.
Regardons à nouveau le graphique de la fonction suivante :
y=log{_3}x
Ceci peut être écrit sous forme exponentielle comme :
3^y=x
Envisageons maintenant l’inverse de cette fonction. Pour ce faire, nous interchangeons x et y :
3^x=y
La fonction exponentielle 3^x=y est une fonction pour laquelle nous pouvons facilement générer des points. Si nous prenons certaines valeurs pour x et les introduisons dans l’équation pour trouver les valeurs correspondantes pour y, nous pouvons obtenir les points suivants :
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) et (3,27)
Nous devons maintenant noter que ces points ne sont pas sur la fonction originale (y=log{_3}x) mais plutôt sur son inverse 3^x=y. Cependant, si nous interchangeons les coordonnées x et y de chaque point, nous obtiendrons en fait une liste de points sur la fonction originale.
Ce sont : (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) et (27,3).
Nous traçons et connectons ces points pour obtenir le graphique de la fonction y=log{_3}x ci-dessous.
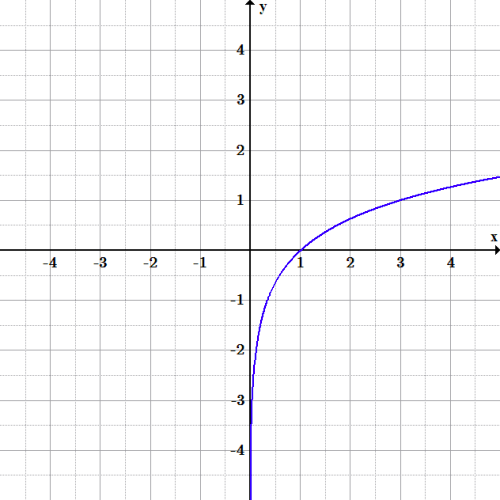
Graphe de y=log{_3}x : Le graphique de la fonction logarithmique en base 3 peut être généré en utilisant l’inverse de la fonction. Sa forme est la même que celle des autres fonctions logarithmiques, juste avec une échelle différente.
Graphie des fonctions logarithmiques dont la base est comprise entre 0 et 1
Jusqu’à présent, nous avons graphié les fonctions logarithmiques dont la base est supérieure à 1. Si nous considérons plutôt les fonctions logarithmiques avec une base b, telle que 0<b<1, nous obtenons un graphique très similaire à ceux que nous avons déjà vus.
En effet, si b>0, le graphe de y=log{_b}x et le graphe de y=log{_\frac{1}{b}}x sont symétriques sur l’axe des x. Ainsi, si l’on identifie un point (x,y) sur le graphe de y=log{_b}x, on peut trouver le point correspondant sur y=log{_\frac{1}{b}}x en changeant le signe de la coordonnée y. Le point correspondant est (x,-). Le point correspondant est (x,-y).
Voici un exemple pour b=2.
Graphes de log{_2}x et de log{_\frac{1}{2}}x : Les graphiques de log_2 x et de log{_\frac{1}{2}x sont symétriques sur l’axe des x
Résolution de problèmes avec des graphiques logarithmiques
Certaines fonctions dont la forme change rapidement sont mieux représentées sur une échelle qui augmente exponentiellement, comme un graphique logarithmique.
Objectifs d’apprentissage
Convertir les problèmes en échelles logarithmiques et discuter des avantages de le faire
Principaux points à retenir
Principaux points
- Les graphiques logarithmiques utilisent des échelles logarithmiques, dans lesquelles les valeurs diffèrent de façon exponentielle. Par exemple, au lieu d’inclure des marques à 0,1,2 et 3, une échelle logarithmique peut inclure des marques à 0,1, 1, 10 et 100, chacune à une distance égale de la précédente et de la suivante.
- Les graphiques logarithmiques permettent de tracer une très grande plage de données sans perdre la forme du graphique.
- Les graphiques logarithmiques facilitent l’interpolation dans des zones qui peuvent être difficiles à lire sur des axes linéaires. Par exemple, si le graphique y=x^5 est mis à l’échelle pour montrer une très large gamme de valeurs de y, la courbure près de l’origine peut être indiscernable sur des axes linéaires. Elle est beaucoup plus claire sur des axes logarithmiques.
Termes clés
- logarithme : Le logarithme d’un nombre est l’exposant par lequel une autre valeur fixe, la base, doit être élevée pour produire ce nombre.
- Interpoler : Estimer la valeur d’une fonction entre deux points entre lesquels elle est tabulée.
Pourquoi utiliser une échelle logarithmique ?
De nombreuses relations mathématiques et physiques dépendent fonctionnellement de variables d’ordre élevé. Cela signifie que pour de petits changements dans la variable indépendante, il y a de très grands changements dans la variable dépendante. Ainsi, il devient difficile de représenter graphiquement de telles fonctions sur l’axe standard.
Considérez, par exemple, la loi de Stefan-Boltzmann, qui relie la puissance (j*) émise par un corps noir à la température (T).
j^*= \sigma T^4
Sur un graphique standard, cette équation peut être assez difficile à manier. La dépendance au quatrième degré de la température signifie que la puissance augmente extrêmement rapidement. Le fait que le taux soit toujours croissant (et de façon abrupte) signifie qu’un changement d’échelle (mise à l’échelle des axes par 5, 10 ou même 100) n’est pas d’une grande aide pour rendre le graphique plus facile à interpréter.
Pour les fonctions très abruptes, il est possible de tracer les points de façon plus fluide tout en conservant l’intégrité des données : on peut utiliser un graphique avec une échelle logarithmique, où au lieu que chaque espace sur un graphique représente une augmentation constante, il représente une augmentation exponentielle. Alors qu’un graphique normal (linéaire) pourrait avoir des intervalles égaux allant de 1, 2, 3, 4, une échelle logarithmique aurait ces mêmes intervalles égaux représentant 1, 10, 100, 1000. Voici quelques exemples de fonctions représentées graphiquement sur une échelle linéaire, une échelle semi-logarithmique et une échelle logarithmique.
Le haut à gauche est une échelle linéaire. La partie inférieure droite est une échelle logarithmique. Les échelles supérieure droite et inférieure gauche sont appelées échelles semi-logarithmiques parce qu’un axe est mis à l’échelle de façon linéaire tandis que l’autre est mis à l’échelle à l’aide de logarithmes.

Échelle logarithmique : Les graphiques des fonctions f(x)=10^x,f(x)=x et f(x)=\log x sur quatre tracés de coordonnées différents. En haut à gauche est une échelle linéaire, en haut à droite et en bas à gauche sont des échelles semi-logarithmiques et en bas à droite est une échelle logarithmique.
Comme vous pouvez le voir, lorsque les deux axes ont utilisé une échelle logarithmique (en bas à droite), le graphique a conservé les propriétés du graphique original (en haut à gauche) où les deux axes ont été mis à l’échelle en utilisant une échelle linéaire. Cela signifie que si nous voulons représenter graphiquement une fonction qui est peu maniable sur une échelle linéaire, nous pouvons utiliser une échelle logarithmique sur chaque axe et conserver les propriétés du graphique tout en le rendant plus facile à représenter.
Avec les échelles semi-logarithmiques, les fonctions ont des formes qui sont biaisées par rapport à l’original. Lorsque seul l’axe des x a une échelle logarithmique, la courbe logarithmique apparaît comme une ligne et les courbes linéaire et exponentielle ont toutes deux un aspect exponentiel. Lorsque seul l’axe des y a une échelle logarithmique, la courbe exponentielle apparaît comme une ligne et les courbes linéaires et logarithmiques apparaissent toutes deux logarithmiques.Il convient de noter que les exemples des graphiques visaient à illustrer un point et que les fonctions représentées graphiquement n’étaient pas nécessairement difficiles à manier sur un ensemble d’axes à échelle linéaire.
Conversion des échelles linéaires en échelles logarithmiques
La principale différence entre les échelles logarithmiques et linéaires est que, si la différence de valeur entre des points linéaires de distance égale reste constante (c’est-à-dire que si l’espace de 0 à 1 sur l’échelle est de 1 cm sur la page, la distance de 1 à 2, 2 à 3, etc, sera la même), la différence de valeur entre les points sur une échelle logarithmique changera de façon exponentielle. Une échelle logarithmique commencera à une certaine puissance de 10, et avec chaque unité, elle augmentera d’une puissance de 10.
Donc, si l’on voulait convertir une échelle linéaire (avec les valeurs 0-5 en une échelle logarithmique, une option serait de remplacer 1,2,3,4 et 5 par 0,001,0,01,0,1,1,10 et 100, respectivement. Entre chaque valeur majeure de l’échelle logarithmique, les points de suspension se rapprochent de plus en plus à mesure que la valeur augmente. Par exemple, dans l’espace entre 1 et 10, les 8 et 9 sont beaucoup plus proches que les 2 et 3.
Les avantages de l’utilisation d’une échelle logarithmique sont doubles. Premièrement, en procédant ainsi, on peut tracer une très large gamme de données sans perdre la forme du graphique. Deuxièmement, cela permet d’interpoler en tout point du graphique, quelle que soit l’étendue du graphique. Des données similaires tracées sur une échelle linéaire sont moins claires.
Résolution de problèmes à l’aide de graphiques logarithmiques
Un point clé de l’utilisation de graphiques logarithmiques pour résoudre des problèmes est qu’ils élargissent les échelles au point où de grandes plages de données ont plus de sens. Dans l’équation mentionnée ci-dessus (j^*= \sigma T^4), tracer j en fonction de T générerait la courbe attendue, mais l’échelle serait telle que les changements infimes passent inaperçus et que les effets à grande échelle de la relation dominent le graphique : Elle est si grande que les » zones intéressantes » ne tiendront pas sur le papier à une échelle lisible.
En prenant le logarithme de chaque côté des équations, on obtient : logj=log{(\sigma\tau ) }^4 . Nous nous appuyons maintenant sur les propriétés des logarithmes pour réécrire l’équation.
Rappelons les propriétés suivantes des logarithmes :
\log(ab)=\log(a)+\log(b) \\\log(a)^b=(b)\log(a)
En utilisant ce qui précède, notre équation devient :
\begin{align} \log j&=4\log{(\sigma\tau ) } \\N &=4\log{(\sigma)}+4\log{(\tau ) } \\N &=4\log{(\tau ) }+4\log{(\sigma)} \end{align}