Une base vectorielle d’un espace vectoriel 
est définie comme un sous-ensemble 
de vecteurs dans 
qui sont linéairement indépendants et couvrent 
. Par conséquent, si 
est une liste de vecteurs dans 
, alors ces vecteurs forment une base vectorielle si et seulement si chaque 
peut être écrit de manière unique comme
 |
(1)
|
où 
sont des éléments du champ de base.
Lorsque le champ de base est le réel de sorte que 
pour 
, les vecteurs de base résultants sont 
-tuples de réels qui couvrent 
espace euclidien à dimension 
. D’autres champs de base possibles incluent les complexes 
, ainsi que divers champs de caractéristique positive considérés en algèbre, en théorie des nombres et en géométrie algébrique.
Un espace vectoriel 
possède de nombreuses bases vectorielles différentes, mais il y a toujours le même nombre de vecteurs de base dans chacune d’elles. Le nombre de vecteurs de base dans 
est appelé la dimension de 
. Chaque liste d’étendue dans un espace vectoriel peut être réduite à une base de l’espace vectoriel.
L’exemple le plus simple d’une base vectorielle est la base standard dans l’espace euclidien 
, dans laquelle les vecteurs de base se trouvent le long de chaque axe de coordonnées. Un changement de base peut être utilisé pour transformer les vecteurs (et les opérateurs) d’une base donnée en une autre.
Donné un hyperplan défini par
 |
(2)
|
une base peut être trouvée en résolvant 
en termes de 
, et 
. En effectuant cette procédure,
 |
(3)
|
alors
 |
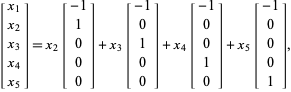(4)
|
et les vecteurs ci-dessus forment une base (non normalisée).
Donné à une matrice 
avec une base orthonormée, la matrice correspondant à un changement de base, exprimée en termes de 
est
 |
(5)
|
Lorsqu’un espace vectoriel est de dimension infinie, alors une base existe tant qu’on suppose l’axiome du choix. Un sous-ensemble de la base qui est linéairement indépendant et dont l’étendue est dense est appelé un ensemble complet, et est similaire à une base. Lorsque 
est un espace de Hilbert, un ensemble complet est appelé une base de Hilbert.