Fonction à pas de Heaviside

.

La fonction échelon de Heaviside est une fonction mathématique notée , ou parfois ou (Abramowitz et Stegun 1972, p. 1020), et également connue sous le nom de « fonction échelon unitaire ». Le terme « fonction échelon de Heaviside » et son symbole peuvent représenter soit une fonction constante par morceaux, soit une fonction généralisée.

Lorsqu’elle est définie comme une fonction constante par morceaux, la fonction d’étape de Heaviside est donnée par

(1)

(Abramowitz et Stegun 1972, p. 1020 ; Bracewell 2000, p. 61). Le tracé ci-dessus montre cette fonction (figure de gauche), et comment elle apparaîtrait si elle était affichée sur un oscilloscope (figure de droite).

Lorsqu’elle est définie comme une fonction généralisée, elle peut être définie comme une fonction telle que

(2)

pour la dérivée d’une fonction suffisamment lisse qui décroît suffisamment vite (Kanwal 1998).

Le langage Wolfram représente la fonction généralisée de Heaviside sous la forme HeavisideTheta, tout en utilisant UnitStep pour représenter la fonction par morceaux Piecewise (qui, notons-le, adopte la convention au lieu de la définition conventionnelle ).

La notation abrégée

(3)

est parfois aussi utilisé.

La fonction échelon de Heaviside est liée à la fonction boxcar par

(4)

et peut être définie en termes de fonction de signe par définie en termes de fonction de signe par

(5)

La dérivée de la la fonction échelon est donnée par

(6)

où est la fonction delta (Bracewell 2000, p. 97).

La fonction échelon de Heaviside est liée à la fonction rampe par

(7)

et à la dérivée de par

(8)

Les deux sont également reliés par

(9)

où désigne la convolution.

Bracewell (2000) donne de nombreuses identités, dont certaines sont les suivantes . En laissant dénoter la convolution,

(10)

.

			(11)
			(12)
			(13)
.			(14)

En outre,

			(15)
.			(16)

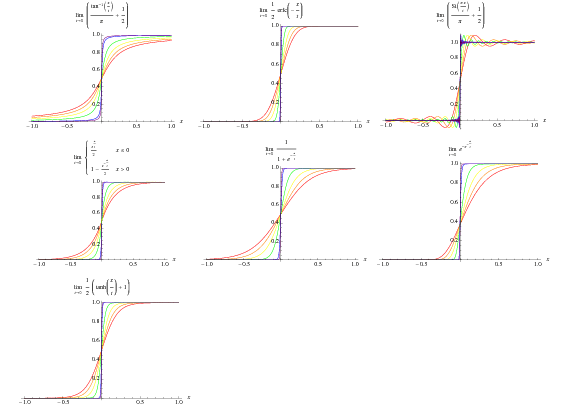
La fonction échelon de Heaviside peut être définie par les limites suivantes,

			(17)
			(18)
			(19)
			(20)
			(21)
			(22)
			(23)
			(24)
.			(25)
.			(26)
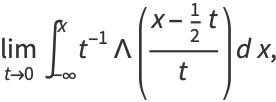			(27)

où est la fonction erfc, est l’intégrale du sinus, est la fonction sinc, et est la fonction triangle à un argument. Les quatre premières sont illustrées ci-dessus pour , 0,1 et 0,01.

Bien sûr, toute fonction monotone avec des asymptotes horizontales inégales constantes est une fonction échelon de Heaviside sous une mise à l’échelle appropriée et une réflexion éventuelle. La transformée de Fourier de la fonction échelon de Heaviside est donnée par

			(28)
			(29)

où est la fonction delta.