Après avoir lu ce chapitre, vous serez en mesure de faire ce qui suit :
- Définir l’erreur aléatoire et la différencier du biais
- Illustrer l’erreur aléatoire à l’aide d’exemples
- Interpréter une valeur p-.valeur
- Interpréter un intervalle de confiance
- Différencier les erreurs statistiques de type 1 et de type 2 et expliquer comment elles s’appliquent à la recherche épidémiologique
- Décrire comment la puissance statistique affecte la recherche
Dans ce chapitre, nous allons couvrir l’erreur aléatoire – d’où elle vient, comment nous la traitons et ce qu’elle signifie pour l’épidémiologie.
Avant tout, l’erreur aléatoire n’est pas un biais. Le biais est une erreur systématique et est abordé plus en détail au chapitre 6.
L’erreur aléatoire est exactement ce qu’elle semble être : des erreurs aléatoires dans les données. Toutes les données contiennent des erreurs aléatoires, car aucun système de mesure n’est parfait. L’ampleur des erreurs aléatoires dépend en partie de l’échelle à laquelle quelque chose est mesuré (les erreurs dans les mesures au niveau moléculaire seraient de l’ordre du nanomètre, alors que les erreurs dans les mesures de la taille humaine sont probablement de l’ordre d’un centimètre ou deux) et en partie de la qualité des outils utilisés. Les laboratoires de physique et de chimie disposent de balances très précises et coûteuses qui peuvent mesurer la masse au gramme, au microgramme ou au nanogramme près, alors que la balance moyenne dans la salle de bain de quelqu’un est probablement précise à une demi-livre ou une livre près.
Pour vous faire une idée de l’erreur aléatoire, imaginez que vous préparez un gâteau qui nécessite 6 cuillères à soupe de beurre. Pour obtenir les 6 cuillères à soupe de beurre (trois quarts de bâton, s’il y a 4 bâtons dans une livre, comme c’est généralement le cas aux États-Unis), vous pourriez utiliser les marques qui apparaissent sur le papier ciré autour du bâton, en supposant qu’elles soient alignées correctement. Vous pouvez aussi suivre la méthode de ma mère, qui consiste à déballer le bâtonnet, à faire une légère marque sur ce qui ressemble à la moitié du bâtonnet, puis à arriver aux trois quarts en évaluant à vue d’œil la moitié de cette moitié. Ou vous pouvez utiliser ma méthode, qui consiste à évaluer à vue d’œil la marque des trois quarts depuis le début et à couper. Toutes ces méthodes de « mesure » vous donneront environ 6 cuillères à soupe de beurre, ce qui est certainement suffisant pour la préparation d’un gâteau, mais probablement pas exactement la valeur de 3 onces, qui est le poids de 6 cuillères à soupe de beurre aux États-Unis. La mesure dans laquelle vous êtes légèrement au-dessus de 3 onces cette fois-ci et peut-être légèrement en dessous de 3 onces la prochaine fois est due à une erreur aléatoire dans votre mesure du beurre. Si vous sous-estimez ou surestimez toujours, il s’agirait alors d’un biais – cependant, vos mesures constamment sous-estimées ou surestimées contiendraient en elles-mêmes une erreur aléatoire.
Pour toute variable donnée que nous pourrions vouloir mesurer en épidémiologie (par ex, la taille, la moyenne générale, la fréquence cardiaque, le nombre d’années passées à travailler dans une usine donnée, le taux de triglycérides sériques, etc.), nous nous attendons à ce qu’il y ait une variabilité dans l’échantillon – c’est-à-dire que nous ne nous attendons pas à ce que tous les membres de la population aient exactement la même valeur. Il ne s’agit pas d’une erreur aléatoire. L’erreur aléatoire (et le biais) se produit lorsque nous essayons de mesurer ces choses. En effet, l’épidémiologie en tant que domaine repose sur cette variabilité inhérente. Si tout le monde était exactement pareil, alors nous ne serions pas en mesure d’identifier quels types de personnes ont un risque plus élevé de développer une maladie particulière.
En épidémiologie, nos mesures reposent parfois sur un humain autre que le participant à l’étude mesurant quelque chose sur ou à propos du participant. Il s’agit par exemple de la mesure de la taille ou du poids, de la pression artérielle ou du cholestérol sérique. Pour certaines de ces mesures (par exemple, le poids et le cholestérol sérique), l’erreur aléatoire se glisse dans les données à cause de l’instrument utilisé – ici, une balance qui a probablement une fluctuation d’une demi-livre, ou un test de laboratoire avec une marge d’erreur de quelques milligrammes par décilitre. Pour d’autres mesures (par exemple, la taille et la pression artérielle), le mesureur lui-même est responsable de toute erreur aléatoire, comme dans l’exemple du beurre.
Cependant, nombre de nos mesures reposent sur l’autodéclaration des participants. Il existe des manuels et des cours entiers consacrés à la conception de questionnaires, et la science derrière la façon d’obtenir les données les plus précises des gens via les méthodes d’enquête est assez bonne. Le Pew Research Center propose un beau tutoriel d’introduction à la conception de questionnaires sur son site web.
Pour ce qui est de notre discussion ici, l’erreur aléatoire apparaîtra également dans les données de questionnaire. Pour certaines variables, il y aura moins d’erreurs aléatoires que d’autres (par exemple, la race autodéclarée est probablement assez précise), mais il y en aura quand même – par exemple, des personnes cochant accidentellement la mauvaise case. Pour d’autres variables, il y aura davantage d’erreurs aléatoires (par exemple, des réponses imprécises à des questions telles que « Au cours de l’année écoulée, combien de fois par mois avez-vous mangé du riz ? »). Une bonne question à se poser lorsqu’on considère la quantité d’erreur aléatoire qui pourrait se trouver dans une variable dérivée d’un questionnaire est la suivante : « Les gens peuvent-ils me dire cela ? » La plupart des gens pourraient théoriquement vous dire combien ils ont dormi la nuit dernière, mais ils seraient bien en peine de vous dire combien ils ont dormi la même nuit il y a un an. Le fait qu’ils vous le disent ou non est une autre question et touche au biais (voir chapitre 6). Quoi qu’il en soit, l’erreur aléatoire dans les données de questionnaire augmente à mesure que la probabilité que les personnes puissent vous donner la réponse diminue.
Quantification de l’erreur aléatoire
Bien que nous puissions – et devions – travailler pour minimiser l’erreur aléatoire (en utilisant des instruments de haute qualité, en formant le personnel sur la façon de prendre des mesures, en concevant de bons questionnaires, etc.), elle ne peut jamais être entièrement éliminée. Heureusement, nous pouvons utiliser les statistiques pour quantifier les erreurs aléatoires présentes dans une étude. En effet, c’est à cela que servent les statistiques. Dans ce livre, je ne couvrirai qu’une petite partie du vaste domaine des statistiques : l’interprétation des valeurs p et des intervalles de confiance (IC). Plutôt que de me concentrer sur la façon de les calculer, je vais plutôt m’intéresser à ce qu’ils signifient (et ce qu’ils ne signifient pas). La connaissance des p-values et des IC est suffisante pour permettre une interprétation précise des résultats des études épidémiologiques pour les étudiants débutants en épidémiologie.
p-values
Lorsque l’on mène une recherche scientifique, quelle qu’elle soit, y compris en épidémiologie, on commence par une hypothèse, qui est ensuite testée au fur et à mesure de l’étude. Par exemple, si nous étudions la taille moyenne des étudiants de premier cycle, notre hypothèse (généralement indiquée par H1) pourrait être que les étudiants masculins sont, en moyenne, plus grands que les étudiantes. Toutefois, à des fins de tests statistiques, nous devons reformuler notre hypothèse sous la forme d’une hypothèse nulle. Dans ce cas, notre hypothèse nulle (généralement indiquée par H0) serait la suivante :
Nous entreprendrions alors notre étude pour tester cette hypothèse. Nous déterminons d’abord la population cible (les étudiants de premier cycle) et tirons un échantillon de cette population. Nous mesurons ensuite la taille et le sexe de toutes les personnes de l’échantillon, et nous calculons la taille moyenne des hommes par rapport à celle des femmes. Nous effectuons ensuite un test statistique pour comparer les hauteurs moyennes des deux groupes. Comme nous avons une variable continue (la taille) mesurée dans 2 groupes (hommes et femmes), nous utiliserions un test t, et la statistique t calculée via ce test aurait une valeur p correspondante, qui est ce qui nous intéresse vraiment.
Disons que dans notre étude, nous trouvons que les étudiants masculins mesurent en moyenne 5 pieds 10 pouces, et que chez les étudiantes, la taille moyenne est de 5 pieds 6 pouces (pour une différence de 4 pouces), et nous calculons une valeur p de 0,04. Cela signifie que s’il n’y a vraiment aucune différence de taille moyenne entre les étudiants masculins et les étudiants féminins (c’est-à-dire si l’hypothèse nulle est vraie) et que nous répétons l’étude (jusqu’à tirer un nouvel échantillon de la population), il y a 4 % de chances que nous trouvions à nouveau une différence de taille moyenne de 4 pouces ou plus.
Il y a plusieurs implications qui découlent du paragraphe ci-dessus. Premièrement, en épidémiologie, nous calculons toujours des valeurs p bilatérales. Ici, cela signifie simplement que les 4 % de chances d’une différence de taille ≥4 pouces ne disent rien sur le groupe qui est plus grand – simplement qu’un groupe (soit les hommes, soit les femmes) sera plus grand en moyenne d’au moins 4 pouces. Deuxièmement, les valeurs p n’ont aucun sens si vous parvenez à recruter l’ensemble de la population dans votre étude. Par exemple, disons que notre question de recherche concerne les étudiants du cours de santé publique 425 (H425, Fondements de l’épidémiologie) pendant le trimestre d’hiver 2020 à l’Oregon State University (OSU). Les hommes ou les femmes sont-ils plus grands dans cette population ? Comme la population est assez petite et que tous les membres sont facilement identifiables, nous pouvons inscrire tout le monde au lieu de devoir nous fier à un échantillon. Il y aura toujours une erreur aléatoire dans la mesure de la taille, mais nous n’utilisons plus de valeur p pour la quantifier. En effet, si nous devions répéter l’étude, nous trouverions exactement la même chose, puisque nous avons effectivement mesuré tous les membres de la population. Les valeurs P ne s’appliquent que si nous travaillons avec des échantillons.
Enfin, notez que la valeur p décrit la probabilité de vos données, en supposant que l’hypothèse nulle est vraie – elle ne décrit pas la probabilité que l’hypothèse nulle soit vraie compte tenu de vos données. Il s’agit d’une erreur d’interprétation courante commise par les lecteurs débutants et expérimentés d’études épidémiologiques. La valeur p ne dit rien sur la probabilité que l’hypothèse nulle soit vraie (et donc, à l’inverse, sur la vérité de votre hypothèse réelle). Elle quantifie plutôt la probabilité d’obtenir les données que vous avez obtenues si l’hypothèse nulle était vraie. C’est une distinction subtile mais très importante.
Significativité statistique
Que se passe-t-il ensuite ? Nous avons une valeur p, qui nous indique la chance d’obtenir nos données compte tenu de l’hypothèse nulle. Mais qu’est-ce que cela signifie réellement en termes de ce qu’il faut conclure sur les résultats d’une étude ? Dans le domaine de la santé publique et de la recherche clinique, la pratique courante consiste à utiliser p ≤ 0,05 pour indiquer la signification statistique. En d’autres termes, des décennies de chercheurs dans ce domaine ont collectivement décidé que si la probabilité de commettre une erreur de type I (nous y reviendrons plus loin) est de 5 % ou moins, nous allons « rejeter l’hypothèse nulle ». En reprenant l’exemple de la taille ci-dessus, nous conclurions donc qu’il existe une différence de taille entre les sexes, du moins chez les étudiants de premier cycle. Pour les valeurs p supérieures à 0,05, nous » ne rejetons pas l’hypothèse nulle » et concluons plutôt que nos données n’ont fourni aucune preuve de l’existence d’une différence de taille entre les étudiants de premier cycle masculins et féminins.
Si p > 0,05, nous ne rejetons pas l’hypothèse nulle. Nous n’acceptons jamais l’hypothèse nulle car il est très difficile de prouver l’absence de quelque chose. « Accepter » l’hypothèse nulle implique que nous avons prouvé qu’il n’y a vraiment aucune différence de taille entre les étudiants masculins et féminins, ce qui n’est pas le cas. Si p > 0,05, cela signifie simplement que nous n’avons pas trouvé de preuve contraire à l’hypothèse nulle – et non pas que ladite preuve n’existe pas. Il se peut que nous ayons obtenu un échantillon bizarre, que nous ayons eu un échantillon trop petit, etc. Il existe tout un domaine de la recherche clinique (la recherche comparative sur l’efficacitévi) qui vise à démontrer qu’un traitement n’est ni meilleur ni pire qu’un autre ; les méthodes de ce domaine sont complexes et la taille des échantillons nécessaires est assez importante. Pour la plupart des études épidémiologiques, nous nous en tenons simplement à l’absence de rejet.
Le seuil de p ≤ 0,05 est-il arbitraire ? Absolument. Il convient de le garder à l’esprit, en particulier pour les valeurs de p très proches de ce seuil. 0,49 est-il vraiment si différent de 0,51 ? Probablement pas, mais ils se trouvent de part et d’autre de cette ligne arbitraire. La taille d’une valeur p dépend de trois facteurs : la taille de l’échantillon, la taille de l’effet (il est plus facile de rejeter l’hypothèse nulle si la véritable différence de taille – si nous mesurons tous les individus de la population, et pas seulement notre échantillon – est de 15 cm plutôt que de 5 cm) et la cohérence des données, le plus souvent mesurée par les écarts types autour des hauteurs moyennes dans les deux groupes. Ainsi, une valeur p de 0,51 pourrait presque certainement être réduite en recrutant simplement plus de personnes dans l’étude (ceci concerne la puissance, qui est l’inverse de l’erreur de type II, discutée ci-dessous). Il est important de garder ce fait à l’esprit lorsque vous lisez des études.
Les tests de signification statistique font partie d’une branche de la statistique appelée statistique fréquentiste.ii Bien qu’extrêmement courante en épidémiologie et dans les domaines connexes, cette pratique n’est généralement pas considérée comme une science idéale, pour un certain nombre de raisons. Tout d’abord, le seuil de 0,05 est totalement arbitraire,iii et un test de signification strict rejetterait l’hypothèse nulle pour p = 0,049 mais ne la rejetterait pas pour p = 0,051, même s’ils sont presque identiques. Deuxièmement, l’interprétation des valeurs p et des intervalles de confiance comporte beaucoup plus de nuances que celles que j’ai abordées dans ce chapitre.iv Par exemple, la valeur p teste en réalité toutes les hypothèses de l’analyse, et pas seulement l’hypothèse nulle, et une valeur p élevée indique souvent simplement que les données ne permettent pas de distinguer entre les nombreuses hypothèses concurrentes. Cependant, étant donné que la santé publique et la médecine clinique requièrent toutes deux des décisions de type oui ou non (Devons-nous consacrer des ressources à cette campagne d’éducation sanitaire ? Faut-il donner ce médicament à ce patient ?), il faut un système pour décider si oui ou non, et le test de signification statistique est actuellement ce système. Il existe d’autres moyens de quantifier l’erreur aléatoire, et les statistiques bayésiennes (qui, au lieu d’une réponse par oui ou par non, donnent une probabilité que quelque chose se produise)ii sont de plus en plus populaires. Néanmoins, comme les statistiques fréquentistes et les tests d’hypothèses nulles restent de loin les méthodes les plus courantes utilisées dans la littérature épidémiologique, elles font l’objet de ce chapitre.
Erreurs de type I et de type II
Une erreur de type I (généralement symbolisée par α, la lettre grecque alpha, et étroitement liée aux valeurs p) est la probabilité que vous rejetiez à tort l’hypothèse nulle – en d’autres termes, que vous » trouviez » quelque chose qui n’est pas vraiment là. En choisissant 0,05 comme seuil de signification statistique, nous, dans les domaines de la santé publique et de la recherche clinique, avons tacitement convenu que nous étions prêts à accepter que 5 % de nos résultats soient en réalité des erreurs de type I, ou faux positifs.
Une erreur de type II (généralement symbolisée par β, la lettre grecque bêta) est l’inverse : β est la probabilité que vous échouiez à tort à rejeter l’hypothèse nulle – en d’autres termes, que vous manquiez quelque chose qui est vraiment là.
La puissance des études épidémiologiques varie considérablement : idéalement, elle devrait être d’au moins 90 % (ce qui signifie que le taux d’erreur de type II est de 10 %), mais elle est souvent beaucoup plus faible. La puissance est proportionnelle à la taille de l’échantillon, mais de manière exponentielle – la puissance augmente avec la taille de l’échantillon, mais pour passer d’une puissance de 90 à 95 %, il faut un saut beaucoup plus important dans la taille de l’échantillon que pour passer d’une puissance de 40 à 45 %. Si une étude ne parvient pas à rejeter l’hypothèse nulle, mais que les données semblent indiquer une différence importante entre les groupes, le problème est souvent que l’étude n’était pas assez puissante et qu’avec un échantillon plus important, la valeur p serait probablement inférieure au seuil magique de 0,05. D’un autre côté, une partie du problème avec les petits échantillons est que vous pourriez, par hasard, avoir obtenu un échantillon non représentatif et que l’ajout de participants supplémentaires ne ferait pas progresser les résultats vers la signification statistique. À titre d’exemple, supposons que nous nous intéressions à nouveau aux différences de taille entre les sexes, mais cette fois-ci uniquement chez les athlètes universitaires. Nous commençons par une très petite étude – une seule équipe masculine et une seule équipe féminine. Si nous choisissons, par exemple, l’équipe de basket-ball masculine et l’équipe de gymnastique féminine, nous avons toutes les chances de trouver une différence énorme dans les hauteurs moyennes, peut-être 18 pouces ou plus. L’ajout d’autres équipes à notre étude entraînerait presque certainement une différence beaucoup plus étroite dans les hauteurs moyennes, et la différence de 18 pouces « trouvée » dans notre petite étude initiale ne tiendrait pas dans le temps.
Intervalles de confiance
Parce que nous avons fixé le niveau de \alpha acceptable à 5%, en épidémiologie et dans les domaines connexes, nous utilisons le plus souvent des intervalles de confiance à 95% (IC 95%). On peut utiliser un IC à 95 % pour effectuer des tests de signification : si l’IC à 95 % n’inclut pas la valeur nulle (0 pour la différence de risque et 1,0 pour les odds ratios, les rapports de risque et les rapports de taux), alors p < 0.05, et le résultat est statistiquement significatif.
Bien que les IC à 95 % puissent être utilisés pour les tests de signification, ils contiennent beaucoup plus d’informations que le simple fait de savoir si la valeur p est <0,05 ou non. La plupart des études épidémiologiques font état d’un IC à 95 % autour de toute estimation ponctuelle qui est présentée. L’interprétation correcte d’un IC à 95 % est la suivante :
Nous pouvons également illustrer cela visuellement:
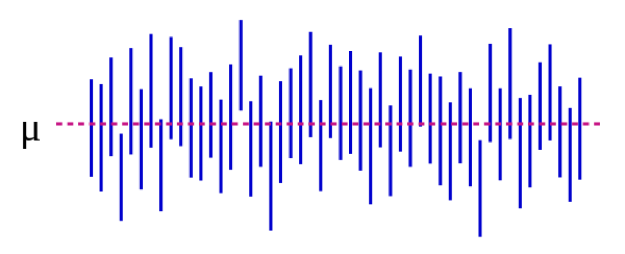
Source : https://es.wikipedia.org/wiki/Intervalo_de_confianza
Dans la figure 5-1, le paramètre de population μ représente la réponse « réelle » que vous obtiendriez si vous pouviez inscrire absolument tout le monde dans la population à l’étude. Nous estimons μ avec les données de notre échantillon. Pour poursuivre avec notre exemple de taille, cela pourrait être 5 pouces : si nous pouvions, comme par magie, mesurer la taille de chaque étudiant de premier cycle aux États-Unis (ou dans le monde, selon la façon dont vous avez défini votre population cible), la différence moyenne entre les étudiants masculins et féminins serait de 5 pouces. Il est important de noter que ce paramètre de population est presque toujours inobservable – il ne devient observable que si vous définissez votre population de manière suffisamment étroite pour pouvoir recruter tout le monde. Chaque ligne verticale bleue représente l’IC d’une « étude » individuelle – 50 dans le cas présent. Les IC varient parce que l’échantillon est légèrement différent à chaque fois – cependant, la plupart des IC (tous sauf 3, en fait) contiennent μ.
Si nous menons notre étude et trouvons une différence moyenne de 4 pouces (IC à 95 %, 1,5 – 7), l’IC nous dit 2 choses. Premièrement, la valeur p de notre test t serait <0,05, puisque l’IC exclut 0 (la valeur nulle dans ce cas, car nous calculons une mesure de différence). Deuxièmement, l’interprétation de l’IC est la suivante : si nous répétons notre étude (y compris le tirage d’un nouvel échantillon) 100 fois, alors 95 fois sur 100, notre IC inclura la valeur réelle (que nous savons ici être de 10 cm, mais que vous ne connaissez pas dans la vie réelle). Ainsi, l’examen de l’IC de 1,5 à 7,0 pouces donne une idée de ce que pourrait être la différence réelle – elle se situe presque certainement quelque part dans cette fourchette, mais pourrait être aussi petite que 1,5 pouce ou aussi grande que 7 pouces. Comme les valeurs p, les IC dépendent de la taille de l’échantillon. Un grand échantillon donnera un IC comparativement plus étroit. Les IC plus étroits sont considérés comme meilleurs car ils donnent une estimation plus précise de ce que pourrait être la » vraie » réponse.
Résumé
L’erreur aléatoire est présente dans toutes les mesures, bien que certaines variables y soient plus sujettes que d’autres. Les valeurs P et les IC sont utilisés pour quantifier l’erreur aléatoire. Une valeur p de 0,05 ou moins est généralement considérée comme » statistiquement significative « , et l’IC correspondant exclut la valeur nulle. Les IC sont utiles pour exprimer la plage potentielle de la valeur » réelle » au niveau de la population qui est estimée.
i. Le beurre aux États-Unis et dans le reste du monde. Errens Kitchen. Mars 2014. https://www.errenskitchen.com/cooking-conversions/butter-measurement-weight-conversions/. Consulté le 26 septembre 2018. (↵ Retour)
ii. Approche bayésienne vs fréquentiste : mêmes données, résultats opposés. 365 Data Sci. août 2017. https://365datascience.com/bayesian-vs-frequentist-approach/. Consulté le 17 octobre 2018. (↵ Retour 1) (↵ Retour 2)
iii. Smith RJ. L’abus continu des tests de signification de l’hypothèse nulle en anthropologie biologique. Am J Phys Anthropol. 2018;166(1):236-245. doi:10.1002/ajpa.23399 (↵ Retour)
iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. Valeurs P et santé reproductive : que peuvent apprendre les chercheurs cliniques de l’American Statistical Association ? Hum Reprod Oxf Engl. 2016;31(11):2406-2410. doi:10.1093/humrep/dew192 (↵ Retour)
v. Greenland S, Senn SJ, Rothman KJ, et al. Tests statistiques, valeurs p, intervalles de confiance et puissance : un guide des interprétations erronées. Eur J Epidemiol. 2016;31:337-350. doi:10.1007/s10654-016-0149-3
vi. Pourquoi la recherche sur l’efficacité comparative est-elle importante ? Institut de recherche sur les résultats centrés sur le patient. https://www.pcori.org/files/why-comparative-effectiveness-research-important. Consulté le 17 octobre 2018. (↵ Retour)
- Il n’y a pas qu’une seule formule pour calculer une valeur p ou un IC. Au contraire, les formules changent en fonction du test statistique qui est appliqué. Tout texte d’introduction à la biostatistique qui traite des méthodes statistiques à utiliser et à quel moment fournirait également les informations correspondantes sur le calcul de la valeur p et de l’IC. ↵
- Ne passez pas trop de temps à essayer de comprendre pourquoi nous avons besoin d’une hypothèse nulle ; nous en avons tout simplement besoin. Le raisonnement est enterré dans des siècles d’arguments académiques de philosophie des sciences. ↵
- Comment choisir le bon test est au-delà de la portée de ce livre – voir n’importe quel livre sur la biostatistique d’introduction ↵
Inhérent à toutes les mesures. » Bruit » dans les données. Sera toujours présent, mais sa quantité dépend de la précision de vos instruments de mesure. Par exemple, les pèse-personnes ont généralement une erreur aléatoire de 0,5 à 1 livre ; les laboratoires de physique contiennent souvent des balances qui n’ont que quelques microgrammes d’erreur aléatoire (celles-ci sont plus chères, et ne peuvent peser que de petites quantités). On peut réduire l’importance de l’erreur aléatoire dans les résultats d’une étude en augmentant la taille de l’échantillon. Cela n’élimine pas l’erreur aléatoire, mais permet au chercheur de mieux voir les données dans le bruit. Corollaire : l’augmentation de la taille de l’échantillon diminuera la valeur p, et réduira l’intervalle de confiance, puisque ce sont des façons de quantifier l’erreur aléatoire.
Erreur systématique. Le biais de sélection découle d’un mauvais échantillonnage (votre échantillon n’est pas représentatif de la population cible), d’un faible taux de réponse des personnes invitées à participer à une étude, d’un traitement différent des cas et des témoins ou des exposés/non exposés, et/ou d’une perte de suivi inégale entre les groupes. Pour évaluer le biais de sélection, il faut se demander « qui ont-ils inclus et qui ont-ils manqué ? » et ensuite se demander « est-ce important » ? Parfois oui, d’autres fois, peut-être pas.
Le biais de mauvaise classification signifie que quelque chose (soit l’exposition, le résultat, un facteur de confusion, ou les trois) a été mesuré de manière incorrecte. Les exemples incluent les personnes qui ne sont pas capables de vous dire quelque chose, les personnes qui ne sont pas disposées à vous dire quelque chose, et une mesure objective qui est en quelque sorte systématiquement erronée (par exemple toujours dans la même direction, comme un brassard de pression sanguine qui n’est pas mis à zéro correctement). Le biais de rappel, le biais de désirabilité sociale, le biais de l’enquêteur – ce sont tous des exemples de biais de classification erronée. Le résultat final de tous ces biais est que des personnes sont placées dans la mauvaise case d’un tableau 2×2. Si l’erreur de classification est répartie de manière égale entre les groupes (par exemple, les personnes exposées et non exposées ont la même chance d’être placées dans la mauvaise case), il s’agit d’une erreur de classification non différentielle. Sinon, il s’agit d’une erreur de classification différentielle.
Un moyen de quantifier l’erreur aléatoire. L’interprétation correcte d’une valeur p est la suivante : la probabilité que, si vous répétiez l’étude (retourner dans la population cible, tirer un nouvel échantillon, tout mesurer, faire l’analyse), vous trouviez un résultat au moins aussi extrême, en supposant que l’hypothèse nulle soit vraie. S’il est vrai qu’il n’y a pas de différence entre les groupes, mais que votre étude a révélé qu’il y avait 15 % de fumeurs en plus dans le groupe A avec une valeur p de 0,06, cela signifie qu’il y a 6 % de chances que, si vous répétez l’étude, vous trouviez à nouveau 15 % (ou un chiffre plus élevé) de fumeurs en plus dans l’un des groupes. Dans le domaine de la santé publique et de la recherche clinique, nous utilisons généralement un seuil de p < 0,05 pour signifier « statistiquement significatif » — ainsi, nous autorisons un taux d’erreur de type I de 5%. Ainsi, dans 5 % des cas, nous » trouverons » quelque chose, même si en réalité il n’y a pas de différence (c’est-à-dire même si en réalité l’hypothèse nulle est vraie). Les autres 95% du temps, nous rejetons correctement l’hypothèse nulle et concluons qu’il y a une différence entre les groupes.
Une façon de quantifier l’erreur aléatoire. L’interprétation correcte d’un intervalle de confiance est la suivante : si vous répétez l’étude 100 fois (retournez dans votre population cible, obtenez un nouvel échantillon, mesurez tout, faites l’analyse), alors 95 fois sur 100, l’intervalle de confiance que vous calculez dans le cadre de ce processus inclura la vraie valeur, en supposant que l’étude ne contient aucun biais. Dans ce cas, la valeur réelle est celle que vous obtiendriez si vous étiez en mesure d’inclure tous les membres de la population dans votre étude – ce qui n’est presque jamais observable, car les populations sont généralement trop grandes pour que tout le monde soit inclus dans un échantillon. Corollaire : Si votre population est suffisamment petite pour que vous puissiez avoir tout le monde dans votre étude, alors le calcul d’un intervalle de confiance est sans objet.
Utilisé dans les tests de signification statistique. L’hypothèse nulle est toujours qu’il n’y a pas de différence entre les deux groupes étudiés.
Test statistique qui détermine si les valeurs moyennes de deux groupes sont différentes.
Méthode quelque peu arbitraire pour déterminer s’il faut croire ou non les résultats d’une étude. En recherche clinique et épidémiologique, la signification statistique est généralement fixée à p < 0,05, soit un taux d’erreur de type I de <5%. Comme pour toutes les méthodes statistiques, ne concerne que l’erreur aléatoire ; une étude peut être statistiquement significative mais non crédible, par exemple, s’il y a une probabilité de biais substantiel. Une étude peut également être statistiquement significative (par exemple, p était < 0,05) mais pas cliniquement significative (par exemple, si la différence de pression artérielle systolique entre les deux groupes était de 2 mm Hg – avec un échantillon suffisamment grand, cela serait statistiquement significatif, mais cela n’a aucune importance sur le plan clinique).
La probabilité qu’une étude « trouve » quelque chose qui n’est pas là. Généralement représentée par α, et étroitement liée aux valeurs p. Habituellement fixée à 0,05 pour les études cliniques et épidémiologiques.
La probabilité que votre étude trouve quelque chose qui est là. Puissance = 1 – β ; bêta est le taux d’erreur de type II. Les petites études, ou les études d’événements rares, sont généralement sous-puissantes.
La probabilité qu’une étude ne trouve pas quelque chose qui était là. Typiquement représentée par β, et étroitement liée à la puissance. Idéalement, elle sera supérieure à 90 % pour les études cliniques et épidémiologiques, bien qu’en pratique, ce ne soit souvent pas le cas.
La mesure de l’association qui est calculée dans une étude. Généralement présentée avec un intervalle de confiance à 95 % correspondant.
.