Frontiers | Rarefaction, Alpha Diversity, and Statistics | Microbiology

Introduction

Les métriques de diversité alpha résument la structure d’une communauté écologique en ce qui concerne sa richesse (nombre de groupes taxonomiques), sa régularité (distribution des abondances des groupes), ou les deux. Étant donné que de nombreuses perturbations d’une communauté affectent la diversité alpha de celle-ci, résumer et comparer la structure de la communauté par le biais de la diversité alpha est une approche omniprésente dans l’analyse des enquêtes sur les communautés. En écologie microbienne, l’analyse de la diversité alpha des données de séquençage amplicon est une première approche commune pour évaluer les différences entre les environnements.

Malheureusement, déterminer comment estimer et comparer de manière significative la diversité alpha n’est pas trivial. À titre d’illustration, considérons l’exemple suivant où la métrique de diversité alpha d’intérêt est la richesse au niveau des souches d’une communauté microbienne (le nombre total de variantes de souches présentes dans l’environnement). Supposons que je réalise une expérience dans laquelle je prélève un échantillon dans l’environnement A et que je compte le nombre de taxons microbiens différents présents dans mon échantillon. Je prélève ensuite un échantillon dans l’environnement B, je compte le nombre de taxons différents dans cet échantillon et je le compare au nombre de taxons dans l’environnement A. Je suis susceptible d’observer un nombre plus élevé de taxons différents dans l’échantillon avec plus de lectures microbiennes. La taille des bibliothèques peut dominer la biologie en déterminant le résultat de l’analyse de la diversité (Lande, 1996).

La raréfaction est une méthode qui ajuste les différences de taille des bibliothèques entre les échantillons pour faciliter les comparaisons de la diversité alpha. Proposée pour la première fois par Sanders (1968), la raréfaction consiste à sélectionner un nombre spécifié d’échantillons qui est égal ou inférieur au nombre d’échantillons du plus petit échantillon, puis à écarter aléatoirement les lectures des échantillons plus grands jusqu’à ce que le nombre d’échantillons restants soit égal à ce seuil (voir Hurlbert, 1971 pour une version déterministe). Sur la base de ces sous-échantillons de taille égale, il est possible de calculer des métriques de diversité qui peuvent contraster les écosystèmes » équitablement « , indépendamment des différences de taille des échantillons (Weiss et al., 2017).

Malheureusement, la raréfaction n’est ni justifiable ni nécessaire, un point de vue encadré statistiquement par McMurdie et Holmes (2014) dans le contexte de la comparaison des abondances relatives. Dans cet article, je discute des raisons pour lesquelles les tailles d’échantillon inégales semblent causer des problèmes particuliers dans l’analyse de la diversité alpha. Je présente une perspective statistique sur l’estimation de la diversité alpha, et je soutiens qu’une vision commune des indices de diversité est à l’origine de problèmes fondamentaux dans la comparaison des échantillons. Sans préconiser un modèle particulier d’échantillonnage microbien, je suggère une approche générale de la comparaison de la diversité microbienne, qui tient compte de l’incertitude dans l’estimation des paramètres de diversité. Cependant, étant donné que les estimations de la diversité alpha sont fortement biaisées lorsque les taxons ne sont pas observés, la comparaison de la diversité alpha à l’aide de données brutes ou raréfiées ne devrait pas être entreprise. Je décris une méthodologie statistique pour l’analyse de la diversité alpha qui s’ajuste aux taxons manquants, qui devrait être utilisée à la place des approches courantes existantes pour l’analyse de la diversité en écologie. Bien que les exemples soient axés sur l’analyse des données du microbiome, les questions et la discussion s’appliquent également à l’analyse des données macroécologiques. En outre, cette discussion s’applique également aux analyses de diversité effectuées au niveau de la souche, de l’espèce ou d’un autre niveau taxonomique.

Erreur de mesure et variance dans les études sur le microbiome

Imaginez que nous ayons une connaissance complète de chaque microbe existant, y compris son identité, son abondance et sa localisation. Pour comparer la diversité microbienne, nous définirions des environnements spécifiques (par exemple, l’intestin distal de femmes âgées de 35 ans vivant dans les États-Unis contigus) et comparerions les métriques de diversité à travers différents gradients écologiques (par exemple, avec ou sans diagnostic de syndrome du côlon irritable). La diversité alpha pourrait être comparée exactement, car nous connaîtrions des populations microbiennes entières avec une précision parfaite.

Malheureusement, nous n’avons pas la connaissance de chaque microbe. Nous prélevons des échantillons dans des environnements, et nous étudions la communauté microbienne présente dans l’échantillon. Nous utilisons nos résultats sur l’échantillon pour tirer des déductions sur l’environnement qui nous intéresse vraiment. Les échantillons ne présentent pas d’intérêt particulier, si ce n’est qu’ils reflètent l’environnement dans lequel ils ont été prélevés. Au fur et à mesure que nous échantillonnons de plus en plus l’environnement en utilisant des échantillons plus grands, nous nous rapprochons de la compréhension de la communauté microbienne réelle et totale qui nous intéresse. Cela signifie qu’à mesure que nous augmentons l’échantillonnage, notre calcul de toute métrique de diversité se rapproche de la valeur de cette métrique de diversité telle qu’elle est calculée en utilisant la population entière.

L’observation de petits échantillons d’une grande population n’est pas un montage expérimental propre à l’écologie microbienne : il est presque universel en statistique. Le montage où l’estimation d’une quantité converge vers la valeur correcte à mesure que l’on obtient plus d’échantillons est également bien compris en statistique. La propriété unique des expériences sur le microbiome et de l’analyse de la diversité alpha est que les échantillons ne représentent pas fidèlement l’ensemble de la communauté microbienne étudiée. Il y a une erreur non ajustée dans l’utilisation de nos échantillons comme procurations pour la communauté entière.

Pour illustrer cette distinction, je contraste les expériences de diversité microbienne avec une expérience non microbienne. Supposons que nous soyons intéressés par la modélisation du flux de CO2 d’un sol traité avec différents amendements. Nous mesurons le flux de sites de taille égale traités avec les différents amendements, en effectuant des répétitions biologiques sur plusieurs sites pour chaque amendement. Pour évaluer si les amendements affectent le flux, nous adapterons un modèle de type régression (tel que l’ANOVA) au flux avec l’amendement comme variable explicative. Implicitement, ce modèle reconnaît que nous pouvons évaluer le flux avec une grande précision, c’est-à-dire que la marge d’erreur pour déterminer le flux est négligeable.

Supposons maintenant que nous sachions que notre machine à mesurer le flux sous-estime systématiquement le flux d’exactement 5 unités. Nous ajusterions l’erreur de mesure en ajoutant 5 unités à chaque mesure avant de les comparer. Mais que se passe-t-il lorsque l’erreur de mesure est aléatoire ? Si l’erreur de mesure de la machine était aléatoire (par exemple, avec une moyenne de 0 et une variance de 1 unité pour tous les amendements), cela n’affecterait aucun amendement particulier. Cependant, la détection d’une différence entre les effets de l’amendement sur le flux serait plus difficile sur le plan statistique : nous aurions besoin de plus d’échantillons pour détecter une véritable différence par rapport au cas sans erreur de mesure. Pour tenir compte du bruit expérimental supplémentaire, nous utiliserions un modèle qui tiendrait compte de l’erreur de mesure dans l’évaluation des différences entre les amendements. Si la variance de l’erreur de mesure était de 1 unité pour l’amendement A mais de 5 unités pour l’amendement B, nous procéderions à un ajustement similaire avec un modèle d’erreur de mesure.

Pour décider si l’erreur de mesure doit être prise en compte lorsque des observations sont effectuées dans une expérience, il est nécessaire de considérer l’effet de la répétition du processus d’observation sur la même unité expérimentale. Dans l’expérience de flux, cela impliquerait de mesurer à nouveau le flux des mêmes sites de sol en utilisant les mêmes conditions expérimentales. Sans erreur de mesure dans les observations, nous observerions systématiquement la même mesure de flux, alors que si nous avions une erreur de mesure aléatoire, nous observerions très probablement des mesures de flux légèrement différentes. Étant donné que les répétitions techniques dans les expériences sur le microbiome produisent différents nombres de lectures, différentes compositions de communautés et différents niveaux de diversité alpha, nous avons une erreur de mesure dans les expériences microbiennes. Nous ne tenons actuellement pas compte de l’erreur de mesure dans les études sur la diversité microbienne.

Bias dans l’estimation et la comparaison de la diversité alpha

Bien que l’erreur de mesure dans les études sur le microbiome affecte toutes les analyses des données du microbiome, la diversité alpha est particulièrement affectée car les estimations de la diversité alpha couramment utilisées sont fortement biaisées par rapport à d’autres problèmes d’estimation en écologie microbienne (comme l’estimation des abondances relatives). Certains outils permettant de résoudre les problèmes de biais dans la diversité alpha existent dans la littérature statistique (Chao et Bunge, 2002 ; Willis et Bunge, 2015 ; Arbel et al., 2016 ; Willis et Martin, 2018). Cependant, deux pratiques incorrectes entourant la diversité alpha empêchent l’adoption de méthodologies motivées par la statistique. La première pratique consiste à utiliser des estimations biaisées des indices de diversité alpha. La seconde pratique consiste à traiter les estimations de la diversité alpha comme des quantités précisément observées qui ne présentent pas d’erreur de mesure.

Pour clarifier cette discussion, je me concentrerai sur la richesse taxonomique (le cas le plus simple), puis je généraliserai l’argument à d’autres mesures de la diversité alpha. Considérons le cadre de la figure 1A, où nous étudions 2 environnements différents, et la richesse de l’environnement A (appelons-la CA) est plus élevée que celle de l’environnement B (CB). Supposons que nous ayons deux répliques biologiques d’échantillons de chaque environnement : nA1 et nA2 lectures de l’environnement A, nB1 et nB2 lectures de l’environnement B, et nA1 < nB1 < nA2 < nB2. Soit cij la richesse observée de l’environnement i sur le réplicat j. Comme cela peut se produire couramment dans la pratique, cA1 < cA2 < cB1 < cB2.

FIGURE 1

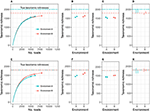
Figure 1. La richesse taxonomique attendue de l’échantillon augmente avec le nombre de lectures (A,E). La comparaison de la richesse taxonomique des échantillons peut donc souvent conduire à des conclusions erronées sur la richesse réelle (B,F). La raréfaction des échantillons au même nombre de lectures peut également conduire à des conclusions incorrectes (C,G). L’ajustement pour les taxons non observés et la prise en compte de l’incertitude de l’estimation permettent de détecter correctement les vraies (D) et les fausses (H) différences de richesse. Si l’exemple employé ici concerne la richesse microbienne, le même argument s’applique à la richesse macroécologique, ainsi qu’aux autres indices de diversité alpha.

Il existe actuellement deux méthodes couramment utilisées pour comparer la diversité alpha. La première méthode, figure 1B, consiste à utiliser les estimations cA1, cA2, cB1 et cB2, et à effectuer la modélisation et les tests d’hypothèse (tels que l’ANOVA) comme si le biais et la variance de ces estimations étaient tous deux nuls (voir, par exemple, Makipaa et al., 2017). Dans le cadre de la figure 1A, cela conduit à la conclusion erronée que l’environnement A a une richesse plus faible que l’environnement B. La deuxième méthode consiste à générer un échantillon normalisé, ou raréfié, en éliminant au hasard les lectures de tous les échantillons jusqu’à ce que chaque échantillon ait nA1 lectures (le nombre de lectures dans le plus petit échantillon), figure 1C. Les niveaux de richesse raréfiés qui en résultent sont alors cA1, cA2′, cB1′, et cB2′. Ces estimations sont ensuite utilisées pour la modélisation et les tests d’hypothèses (voir, par exemple, Arora et al., 2017). Cela permet de conclure que l’environnement A et l’environnement B n’ont pas de richesses significativement différentes, et que les estimations de la richesse sont bien inférieures aux richesses réelles de chaque écosystème (il existe un biais négatif important dans les estimations), ce qui interdit la comparaison de la richesse entre les différentes expériences. De plus, toutes les informations collectées dans les échantillons n’ont pas été utilisées pour effectuer la comparaison.

Je plaide ici pour une troisième stratégie : ajuster la richesse de l’échantillon de chaque écosystème en y ajoutant une estimation du nombre d’espèces non observées, estimer la variance de l’estimation de la richesse totale, et comparer les diversités par rapport à ces erreurs (figure 1D). Cette option présente les avantages de tirer parti de toutes les lectures observées, de comparer les estimations du paramètre réel d’intérêt (la richesse taxonomique) et de tenir compte du bruit expérimental. Dans le cas où les environnements ont une richesse égale (figures 1E-H), cette approche détecte correctement une richesse égale, même lorsque les structures d’abondance diffèrent.

Modéliser les paramètres observés avec une erreur d’estimation n’est pas une nouvelle suggestion : cette approche provient du domaine de la méta-analyse statistique, où les résultats de plusieurs études estimant la même taille d’effet sont comparés (Demidenko, 2004 ; Willis et al., 2016 ; Washburne et al., 2018). Dans les méta-analyses, il faut accorder plus de poids aux études de grande taille pour déterminer la taille de l’effet global, ce qui est intégré dans une méta-analyse via les erreurs standard plus petites sur les estimations de la taille de l’effet. De même, lors de la comparaison de la réponse de différents groupes de traitement dans les essais cliniques, le nombre de sujets dans chaque groupe de traitement est pris en compte dans la comparaison de l’effet global du traitement. L’ajustement de la taille de l’échantillon lors de la comparaison de différents groupes d’observations sans rejeter de données est largement répandu dans les sciences, et le rejet de données pour ajuster des tailles d’échantillon inégales est l’exception. La stratégie décrite ici pour modéliser la richesse après avoir ajusté les espèces manquantes ajuste à la fois le biais et la variance, tenant ainsi compte des différences de taille des bibliothèques et des enquêtes microbiennes incomplètes.

Bien que l’exemple discuté ici soit la richesse, cette approche pour estimer et comparer la diversité alpha en utilisant une correction du biais (incorporant les taxons non observés) et un ajustement de la variance (modèle d’erreur de mesure) pourrait s’appliquer à toute métrique de diversité alpha. Cependant, l’estimation de la richesse fait l’objet d’une littérature statistique bien étudiée, et des estimateurs de richesse adaptés aux données du microbiome existent (voir Bunge et al., 2014 pour une revue). Il n’en va pas de même pour les autres métriques de diversité alpha. Par exemple, les estimateurs Chao-Bunge (Chao et Bunge, 2002) et breakaway (Willis et Bunge, 2015) de la richesse taxonomique fournissent des estimations de la variance, tiennent compte des taxons non observés et ne sont pas trop sensibles au nombre de singleton (le nombre d’espèces observées une fois). En revanche, l’estimateur de l’entropie ajustée à la couverture de l’indice de Shannon (Chao et Shen, 2003) fournit des estimations de la variance et tient compte des taxons non observés, mais il est extrêmement sensible au nombre de singleton, qui est souvent difficile à déterminer dans les études sur le microbiome. Bien que l’estimation de la diversité alpha pour les microbiomes soit un domaine de recherche actif en statistique (Arbel et al., 2016 ; Zhang et Grabchak, 2016 ; Willis et Martin, 2018), il reste de nombreuses caractéristiques des écosystèmes microbiens (telles que la diaphonie entre les échantillons et l’organisation spatiale des microbes) qui ne sont pas encore intégrées dans la méthodologie statistique d’estimation de la diversité alpha. Malgré cela, les estimations de la diversité alpha qui tiennent compte des taxons non observés et fournissent des estimations de la variance sont largement préférables aux estimations plug-in et raréfiées, qui ne tiennent pas compte des taxons non observés et ne fournissent pas d’estimations de la variance.

Discussion

Les estimations plug-in de nombreux indices de diversité alpha (notamment la richesse et la diversité de Shannon) sont biaisées négativement pour le paramètre de diversité alpha de l’environnement, c’est-à-dire qu’elles sous-estiment la véritable diversité alpha (Lande, 1996). Tenter de résoudre ce problème en utilisant la raréfaction induit en fait plus de biais. Ceci est parfois justifié en affirmant que les estimations raréfiées sont également biaisées. Cependant, ce n’est généralement pas vrai, car les environnements peuvent être identiques en ce qui concerne une mesure de diversité alpha, mais les différentes structures d’abondance induiront des biais différents lors de la raréfaction. Par exemple, la figure 1E montre deux environnements avec des structures d’abondance différentes mais une richesse égale ; la raréfaction donne la fausse impression d’une richesse inégale (voir aussi Lande et al., 2000). De cette façon, la richesse de l’échantillon et la richesse raréfiée sont déterminées par des artefacts de l’expérience (taille de la bibliothèque), et non par la structure pure de la communauté microbienne. Afin de tirer des conclusions significatives sur l’ensemble de la communauté microbienne, il est nécessaire d’ajuster l’échantillonnage non exhaustif en utilisant des estimations de paramètres statistiquement motivées pour la diversité alpha. Afin de tirer des conclusions significatives concernant les comparaisons de communautés microbiennes, il est nécessaire d’utiliser des modèles d’erreur de mesure pour ajuster l’incertitude de l’estimation de la diversité alpha.

Il a récemment été avancé que l’étude de la diversité microbienne sans contexte nous détourne de la compréhension des mécanismes écologiques (Shade, 2016). À cette critique, j’ajoute que la mauvaise application des outils statistiques nuit à de nombreuses analyses de la diversité alpha. J’encourage les écologistes microbiens à utiliser des estimations de la diversité alpha qui tiennent compte des espèces non observées, et à utiliser la variance des estimations dans les modèles d’erreur de mesure pour comparer la diversité entre les écosystèmes.

Contributions de l’auteur

AW a rédigé le manuscrit et a effectué l’analyse des données.

Financement

AW est soutenu par des fonds de démarrage accordés par le département de biostatistique de l’Université de Washington, et les National Institutes of Health (R35GM133420).

Conflit d’intérêts

L’auteur déclare que la recherche a été menée en l’absence de toute relation commerciale ou financière qui pourrait être interprétée comme un conflit d’intérêts potentiel.

Remerciements

Cet article est basé sur des notes de cours présentées par l’auteur au Marine Biological Laboratory lors du cours STAMPS en 2013, 2014, 2015, 2016, 2017 et 2018. L’auteur est reconnaissant envers Berry Brosi, le MBL, les directeurs du cours STAMPS et les participants au cours STAMPS pour les innombrables discussions sur ce sujet. L’auteur remercie également Thea Whitman et deux arbitres pour leurs nombreuses suggestions réfléchies sur le manuscrit. Ce manuscrit a été publié en tant que preprint via bioRxiv (Willis, 2017).

Arbel, J., Mengersen, K., et Rousseau, J. (2016). Modèle bayésien non paramétrique dépendant pour des données partiellement répliquées : l’influence des déversements de carburant sur la diversité des espèces. Ann. Appl. Stat. 10, 1496-1516. doi : 10.1214/16-AOAS944