Une 
matrice 
est une matrice orthogonale si
 |
(1)
|
où 
est la transposée de 
et 
est la matrice identité. En particulier, une matrice orthogonale est toujours inversible, et
 |
(2)
|
Sous forme de composant,
 |
(3)
|
Cette relation rend les matrices orthogonales particulièrement faciles à calculer avec, puisque l’opération de transposition est beaucoup plus simple que le calcul d’un inverse.
Par exemple ,
 |
 |
 |
(4)
|
 |
 = |
 |
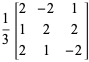(5)
|
sont des matrices orthogonales.
Une matrice 
peut être testée pour voir si elle est orthogonale dans le Wolfram Language en utilisant OrthogonalMatrixQ.
Les lignes d’une matrice orthogonale constituent une base orthonormale. C’est-à-dire que chaque ligne a une longueur de un, et sont mutuellement perpendiculaires. De même, les colonnes constituent également une base orthonormée. En fait, étant donné toute base orthonormale, la matrice dont les rangées sont cette base est une matrice orthogonale. Il en résulte automatiquement que les colonnes sont une autre base orthonormée.
Les matrices orthogonales sont précisément les matrices qui préservent l’innerproduct
 |
(6)
|
Aussi, le déterminant de 
est soit 1, soit 
. En tant que sous-ensemble de 
, les matrices orthogonales ne sont pas connectées puisque le déterminant est une fonction continue. Au lieu de cela, il y a deux composantes correspondant au fait que le déterminant est 1 ou 
. Les matrices orthogonales avec 
sont des rotations, et une telle matrice est appelée matrice orthogonale spéciale.
Le produit matriciel de deux matrices orthogonales est une autre matrice orthogonale. De plus, l’inverse d’une matrice orthogonale est une matrice orthogonale, tout comme la matrice identité. Par conséquent, l’ensemble des matrices orthogonales forment un groupe, appelé groupe orthogonal 
.