Dans notre leçon précédente, nous avons étudié comment utiliser la règle de Cramer avec deux variables. Notre objectif ici est d’étendre l’application de la règle de Cramer à trois variables généralement en termes de \large{x}, \large{y}, et \large{z}. Je vais passer en revue cinq (5) exemples travaillés pour vous aider à vous familiariser avec ce concept.
Pour bien réussir ce sujet, vous devez avoir une idée sur la façon de trouver le déterminant d’une matrice 3⨉3. C’est donc ce que nous allons faire dans un premier temps. Vous êtes prêts ?
Formule pour trouver le déterminant d’une matrice 3⨉3
.
- Donné une matrice 3⨉3

- Son déterminant peut être calculé à l’aide de la formule suivante.
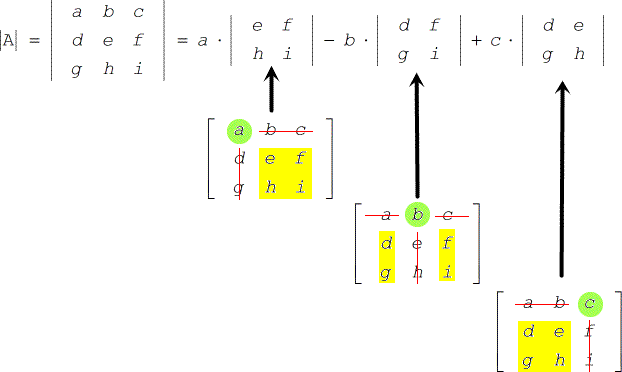
Faisons un exemple rapide.
Trouver le déterminant de la matrice A
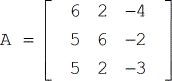
Solution : Assurez-vous de suivre attentivement la formule sur la façon de trouver le déterminant d’une matrice 3×3, comme indiqué ci-dessus. De plus, ne vous précipitez pas lorsque vous effectuez les opérations arithmétiques requises à chaque étape. C’est là que les erreurs courantes se produisent généralement, mais elles peuvent être évitées. Lorsque vous le faites correctement, votre solution devrait être similaire à celle ci-dessous.
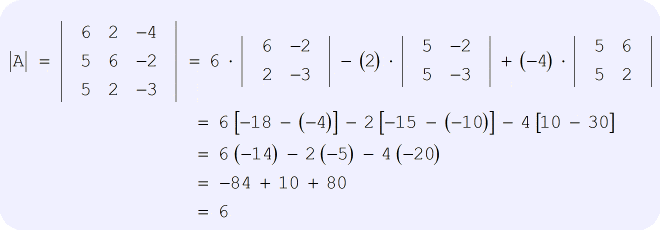
Maintenant, il est temps de passer en revue la procédure sur la façon d’utiliser la règle de Cramer dans un système linéaire impliquant trois variables.
Règle de Cramer pour les systèmes d’équations linéaires à trois variables
- Donné. un système linéaire

- Étiquetage de chacune des quatre matrices
matrice des coefficients :
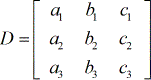
X – matrice :
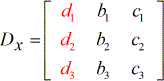
Y – matrice :
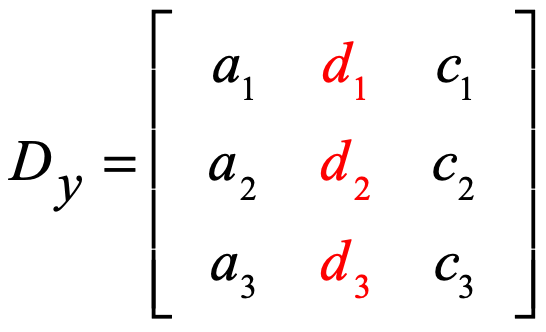
Z – matrice :
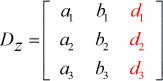
- Pour résoudre x :
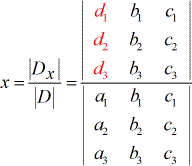
- Pour résoudre y :
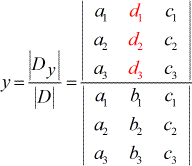
- Pour résoudre z :
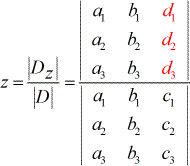
Ce qu’il faut observer dans le montage ci-dessus :
1) Les coefficients des variables x, y et z font appel respectivement aux indices a, b et c. Tandis que les termes constants utilisent l’indice d.
2) Les dénominateurs pour trouver les valeurs de x, y et z sont tous les mêmes qui est le déterminant de la matrice des coefficients (coefficients provenant des colonnes de x, y et z).
3) Pour résoudre x, on remplace les coefficients de la colonne x par la colonne constante (en rouge).
4) Pour résoudre y, on remplace les coefficients de la colonne y par la colonne constante (en rouge).
5) De la même manière, pour résoudre z, les coefficients de la colonne z sont remplacés par la colonne constante (en rouge).
Exemples de résolution de systèmes d’équations linéaires à trois variables par la règle de Cramer
Exemple 1 : Résoudre le système à trois variables par la règle de Cramer.
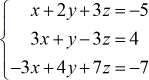
À partir du système d’équations linéaires donné, je construirai les quatre matrices qui seront utilisées pour résoudre les valeurs de \large{\color{green}x}, \large{\color{green}y}, et \large{\color{green}z}.
Utilisez le guide ci-dessus pour configurer correctement ces matrices spéciales.
- matrice des coefficients
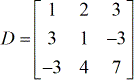
- X – matrice
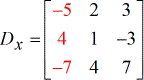
- Y – matrice
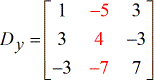
- Z – matrice
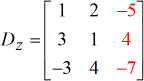
Après, je vais résoudre le déterminant de chaque matrice. Pour ce faire, je peux résoudre manuellement le déterminant de chaque matrice sur papier en utilisant la formule fournie ci-dessus. Cela peut être fastidieux, mais ce n’est pas grave puisque de bonnes compétences en mathématiques se développent en faisant beaucoup de problèmes.
Les valeurs des déterminants sont listées ci-dessous.
Déterminants de chaque matrice:
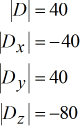
Les réponses ou solutions finales sont facilement calculées ou calculées une fois que tous les déterminants requis sont trouvés.
Valeurs résolues pour \large{\color{green}x}, \large{\color{green}y} et \large{\color{green}z}.
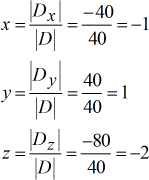
La réponse finale écrite en notation ponctuelle est \color{blue}\left( {x,y,z} \right) = \left( { – 1,1, – 2} \right).
Exemple 2 : Résolvez le système à trois variables par la règle de Cramer.
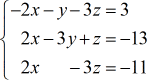
Je considère en fait la matrice des coefficients comme la matrice « primaire » car les trois autres matrices en sont dérivées. Par exemple, la matrice x est juste la matrice « primaire » avec la colonne x remplacée par la colonne constante (en rouge). Vous pouvez observer que le même schéma est appliqué pour construire les autres matrices : y et z.
- matrice coefficient
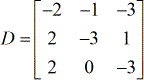
- X – matrice
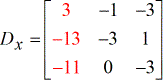
- Y – matrice
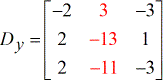
- Z – matrice
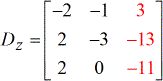
Après avoir résolu le déterminant de chaque matrice, je les ai toutes écrites.
Déterminants de chaque matrice:
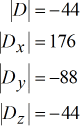
Les valeurs de x, y et z sont calculées comme suit. Remarquez que x est obtenu en prenant le déterminant de la matrice x divisé par le déterminant de la matrice des coefficients. Cette règle vaut pour le reste.
Valeurs résolues pour \large{\color{green}x}, \large{\color{green}y} et \large{\color{green}z}.
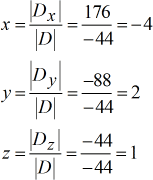
Notre réponse finale est \color{blue}\left( {x,y,z} \right) = \left( { – \,4,2,1} \right).
Exemple 3 : Résoudre le système à trois variables par la règle de Cramer.
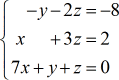
Ce problème est beaucoup plus facile que les deux premiers exemples en raison de la présence d’entrées nulles dans les colonnes x, y et constante. Vous le voyez ? Lorsque nous avons des entrées nulles dans une matrice, le calcul de son déterminant est considérablement simplifié.
En fait, lorsque vous augmentez le nombre de zéros dans une matrice carrée, le travail effectué pour trouver son déterminant est considérablement réduit.
Voici les matrices extraites du système d’équations linéaires.
- matrice des coefficients
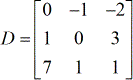
- X – matrice
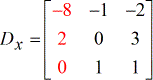
- Y – matrice
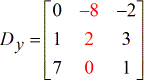
- Z – matrice
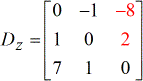
En résolvant leurs déterminants, j’ai obtenu les valeurs suivantes .
Déterminants de chaque matrice :
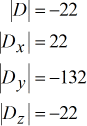
Cela nous amène à mettre en place et à calculer facilement les réponses finales.
Valeurs résolues de \large{\color{green}x}, et \large{\color{green}y}, et \large{\color{green}z}.
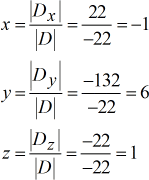
La réponse finale est \color{blue}\left( {x,y,z} \right) = \left( { – \,1,6,1} \right).
Exemple 4 : Résoudre le système à trois variables par la règle de Cramer
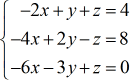
Écrivez les quatre matrices spéciales.
- matrice de coefficient
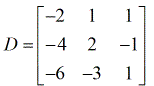
- X – matrice
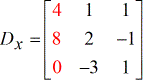
- Y – matrice
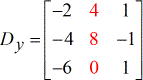
- Z – matrice
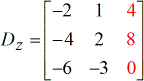
Evaluez chaque matrice pour trouver son déterminant.
Voici les déterminants de chaque matrice :
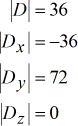
Utiliser la règle de Cramer pour obtenir les solutions suivantes.
Valeurs résolues de \large{\color{green}x}, \large{\color{green}y} et \large{\color{green}z}.
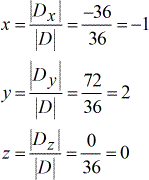
La réponse finale est \color{blue}\left( {x,y,z} \right) = \left( { – \,1,2,0} \right).
Exemple 5 : Résoudre le système à trois variables par la règle de Cramer
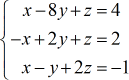
Faisons un dernier exemple ! J’espère qu’à ce stade, vous avez eu suffisamment de pratique sur la façon de résoudre des systèmes à trois variables en utilisant la règle de Cramer.
Je vous suggère de résoudre d’abord ceci sur papier et de revenir ensuite pour comparer votre réponse. Ne vous inquiétez pas, personne ne regarde. 👀 Lorsque vous êtes prêt, faites défiler vers le bas pour voir la solution.

Construire les quatre matrices spéciales.
- matrice des coefficients
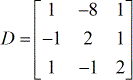
- X – matrice
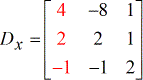
- Y – matrice
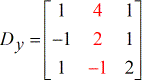
- Z – matrice
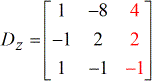
Trouver le déterminant de chaque matrice carrée.
Déterminants de chaque matrice
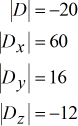
Solvez pour x, y et z en utilisant la formule donnée.
Valeurs résolues pour \large{\color{green}x}, \large{\color{green}y} et \large{\color{green}z}.
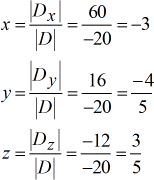
Fait ! La réponse finale sous forme de points est \color{blue}\left( {x,y,z} \right) = {\large{\left( { – \,3, – {4 \over 5},{3 \over 5}} \right)}}.
Pratique avec les feuilles de travail
Vous pourriez également être intéressé par :
La règle de Cramer 2×2