Introduction
L’analyse de régression est couramment utilisée pour modéliser la relation entre une seule variable dépendante Y et un ou plusieurs prédicteurs. Lorsque nous avons un seul prédicteur, nous appelons cela une régression linéaire « simple » :
E = β0 + β1X
C’est-à-dire que la valeur attendue de Y est une fonction linéaire de X. Les bêtas sont sélectionnés en choisissant la ligne qui minimise la distance au carré entre chaque valeur Y et la ligne de meilleur ajustement. Les bêtas sont choisis de telle sorte qu’ils minimisent cette expression :
∑i (yi – (β0 + β1X))2
Un graphique instructif que j’ai trouvé sur Internet
. graphique que j’ai trouvé sur Internet

Source : http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Lorsque nous avons plus d’un prédicteur, nous parlons de régression linéaire multiple :
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
Les valeurs ajustées (c’est-à-dire, les valeurs prédites) sont définies comme les valeurs de Y qui sont générées si nous branchons nos valeurs X dans notre modèle ajusté.
Les résidus sont les valeurs ajustées moins les valeurs réelles observées de Y.
Voici un exemple de régression linéaire avec deux prédicteurs et un résultat :
Au lieu de la » ligne de meilleur ajustement « , il existe un » plan de meilleur ajustement « .
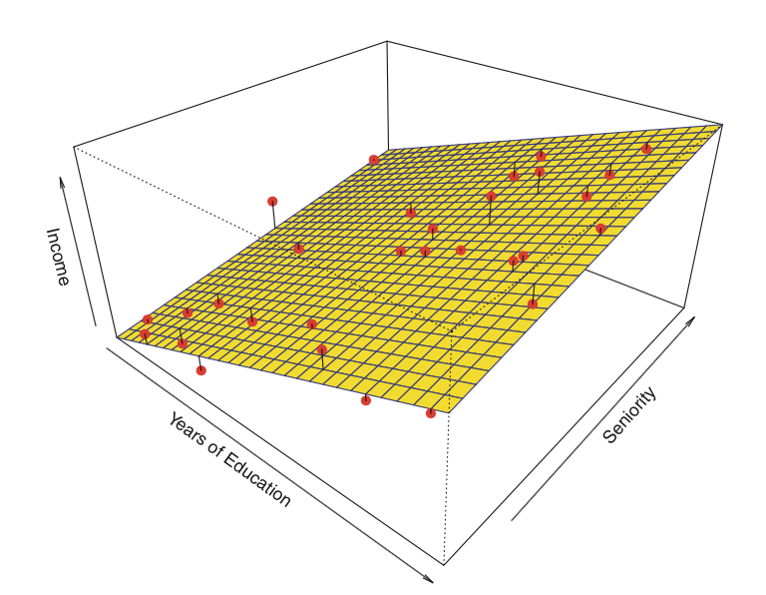
Source : James et al. Introduction to Statistical Learning (Springer 2013)
Il existe quatre hypothèses associées à un modèle de régression linéaire :
- Linéarité : La relation entre X et la moyenne de Y est linéaire.
- Homoscédasticité : La variance du résidu est la même pour toute valeur de X.
- Indépendance : Les observations sont indépendantes les unes des autres.
- Normalité : Pour toute valeur fixe de X, Y est normalement distribué.
Nous examinerons comment évaluer ces hypothèses plus tard dans le module.
Débutons par une régression simple. Dans R, les modèles sont généralement ajustés en appelant une fonction d’ajustement de modèle, dans notre cas lm(), avec un objet « formula » décrivant le modèle et un objet « data.frame » contenant les variables utilisées dans la formule. Un appel typique peut ressembler à
> mafonction <- lm(formule, données, …)
et elle renverra un objet modèle ajusté, ici stocké sous le nom de mafonction. Ce modèle ajusté peut ensuite être imprimé, résumé ou visualisé ; de plus, les valeurs ajustées et les résidus peuvent être extraits, et nous pouvons faire des prédictions sur de nouvelles données (valeurs de X) calculées à l’aide de fonctions telles que summary(), residuals(),predict(), etc. Ensuite, nous verrons comment ajuster une régression linéaire simple.
Retour en haut | page précédente | page suivante
.