Test d’adéquation : Qu’est-ce que c’est ?

Définitions statistiques > Tests d’adéquation

Le test d’adéquation est utilisé pour tester si les données d’un échantillon correspondent à une distribution d’une certaine population (c’est-à-dire.c’est-à-dire une population avec une distribution normale ou une population avec une distribution de Weibull). En d’autres termes, il vous indique si les données de votre échantillon représentent les données que vous vous attendez à trouver dans la population réelle. Les tests de qualité d’ajustement couramment utilisés en statistique sont :

• Le chi-deux.
• Kolmogorov-Smirnov.
• Anderson-Darling.
• Shipiro-Wilk.

Le test d’adéquation du chi carré

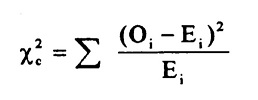
La formule du chi carré.

Le test du chi carré est le plus courant des tests d’adéquation et c’est celui que vous rencontrerez dans les statistiques AP ou les statistiques élémentaires. Le chi carré peut être utilisé pour des distributions discrètes comme la distribution binomiale et la distribution de Poisson, tandis que les tests d’adéquation de Kolmogorov-Smirnov et d’Anderson-Darling ne peuvent être utilisés que pour des distributions continues.

Deux inconvénients potentiels du chi carré sont :
1. Le test du chi carré ne peut être utilisé que pour des données mises en classes (bins). Si vous avez des données non classées, vous devrez faire un tableau de fréquence ou un histogramme avant de réaliser le test.
2. Un autre inconvénient du test du chi carré est qu’il nécessite une taille d’échantillon suffisante pour que l’approximation du chi carré soit valide.

Il existe un autre type de test du chi carré, appelé test du chi carré pour l’indépendance. Les deux sont parfois confondus mais ils sont bien différents.

• Le test du chi-deux pour l’indépendance compare deux ensembles de données pour voir s’il existe une relation.
• La qualité d’ajustement du chi-deux consiste à ajuster une variable catégorielle à une distribution.

Les deux tests utilisent la statistique du chi carré et la distribution. Pour plus d’informations sur le calcul de la statistique du chi carré, consultez :
La statistique du test du chi carré (comprend les calculs) : Qu’est-ce qu’une statistique du chi carré ?

Exécution du test

Typiquement, ce test est exécuté à l’aide d’un logiciel. L’hypothèse nulle du test d’adéquation du chi carré est que les données proviennent d’une distribution spécifiée. L’hypothèse alternative est que les données ne proviennent pas d’une distribution spécifiée.

Pour interpréter le test, vous devrez choisir un niveau alpha (1%, 5% et 10% sont courants). Le test du chi-deux renverra une valeur p. Si la valeur p est petite (inférieure au niveau de signification), vous pouvez rejeter l’hypothèse nulle selon laquelle les données proviennent de la distribution spécifiée.

Tests de qualité d’ajustement moins courants utilisés en statistique élémentaire

Kolmogorov-Smirnov

Bien que ce test soit appelé test de normalité, il ne vous dit pas en fait si un échantillon particulier provient probablement d’une population normale. Au lieu de cela, il vous indique quand il est peu probable que vous ayez une distribution normale. L’un des avantages de ce test est qu’il ne fait aucune hypothèse sur la distribution des données. Un échantillon peut être comparé à une distribution en utilisant un test K-S à un échantillon ou un test K-S à deux échantillons. Le test est généralement réalisé à l’aide d’un logiciel (comme SPSS), car les valeurs critiques doivent être calculées pour chaque distribution et trouver les tableaux de valeurs critiques n’est pas une tâche facile. Ce test est généralement recommandé pour les grands échantillons de plus de 2000 personnes. Pour les échantillons plus petits, utilisez Shapiro-Wilk.

Anderson-Darling

Ce test est une modification de Kolmogorov-Smirnov. Il est plus sensible aux déviations des queues d’une distribution. Comme le Kolmogorov-Smirnov, ce test vous indiquera quand il est peu probable que vous ayez une distribution normale et est normalement exécuté à l’aide d’un logiciel statistique.

Shapiro-Wilk

Ce test calcule une valeur W qui vous dira si un échantillon aléatoire provient d’une population normalement distribuée. Ce test est recommandé pour les échantillons jusqu’à n=2000.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL : CRC Press, pp. 536 et 571, 2002.
Dodge, Y. (2008). L’encyclopédie concise de la statistique. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Vogt, W.P. (2005). Dictionnaire des statistiques & Méthodologie : Un guide non technique pour les sciences sociales. SAGE.

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !