Ressources connexes : science des matériaux
Équation de définition du coefficient de Poisson
Résistance des matériaux
Le coefficient de Poisson est défini comme le négatif du rapport entre la déformation latérale et la déformation axiale pour un état de contrainte uniaxiale. Si une charge de traction est appliquée à un matériau, celui-ci s’allonge dans l’axe de la charge (perpendiculairement au plan de la contrainte de traction), comme l’illustre la figure 1 (a). À l’inverse, si la charge est compressive, la dimension axiale diminue, comme l’illustre la figure 1 (b). Si le volume est constant, une contraction ou une expansion latérale correspondante doit se produire. Cette variation latérale aura une relation fixe avec la déformation axiale. La relation, ou le rapport, entre la déformation latérale et la déformation axiale est appelée ratio de Poisson, du nom de son découvreur. Il est généralement symbolisé par v.
Rapport de Poisson des métaux et des matériaux courants
|
Équation du rapport de Poisson :
|
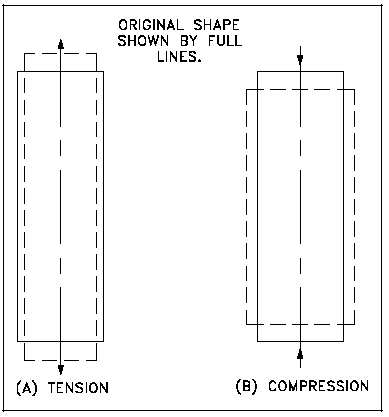 Figure 1
|
Note : Le coefficient de Poisson n’a pas d’unités
Le coefficient de Poisson est parfois aussi appelé le rapport des valeurs absolues de la déformation latérale et axiale. Ce rapport, comme la déformation, est sans unité puisque les deux déformations sont sans unité. Pour les contraintes situées dans le domaine élastique, ce rapport est approximativement constant. Pour un matériau élastique parfaitement isotrope, le coefficient de Poisson est de 0,25, mais pour la plupart des matériaux, la valeur est comprise entre 0,28 et 0,33. En général, pour les aciers, le coefficient de Poisson aura une valeur d’environ 0,3. Cela signifie que s’il y a un pouce par pouce de déformation dans la direction où la contrainte est appliquée, il y aura 0,3 pouce par pouce de déformation perpendiculaire à la direction où la force est appliquée.
![]()
