Leerdoelen
Aan het eind van dit deel zul je in staat zijn om:
- Een scenario uitleggen waarin het magnetische en elektrische veld elkaar kruisen en hun krachten elkaar in evenwicht houden als een geladen deeltje door een snelheidselector beweegt
- Vergelijken hoe ladingsdragers bewegen in een geleidend materiaal en uitleggen hoe dit verband houdt met het Hall-effect
In 1879, bedacht E.H. Hall een experiment dat kan worden gebruikt om het teken van de overheersende ladingsdragers in een geleidend materiaal te bepalen. Vanuit historisch perspectief was dit experiment het eerste dat aantoonde dat de ladingsdragers in de meeste metalen negatief zijn.
Bezoek deze website voor meer informatie over het Hall-effect.
We onderzoeken het Hall-effect door de beweging van de vrije elektronen langs een metalen strook met een breedte l in een constant magnetisch veld te bestuderen (figuur \(\PageIndex{1})). De elektronen bewegen van links naar rechts, dus de magnetische kracht die ze ondervinden duwt ze naar de onderkant van de strook. Hierdoor blijft aan de bovenrand van de strook een overmaat aan positieve lading over, wat resulteert in een elektrisch veld E dat van boven naar beneden is gericht. De ladingsconcentratie aan beide randen neemt toe totdat de elektrische kracht op de elektronen in de ene richting in evenwicht is met de magnetische kracht op hen in de tegenovergestelde richting. Het evenwicht is bereikt wanneer:
waarbij e de grootte is van de elektronlading, \(v_d\) de voortbewegingssnelheid van de elektronen, en E de grootte is van het elektrisch veld dat door de gescheiden lading wordt opgewekt. Als we dit oplossen voor de voortbewegingssnelheid krijgen we
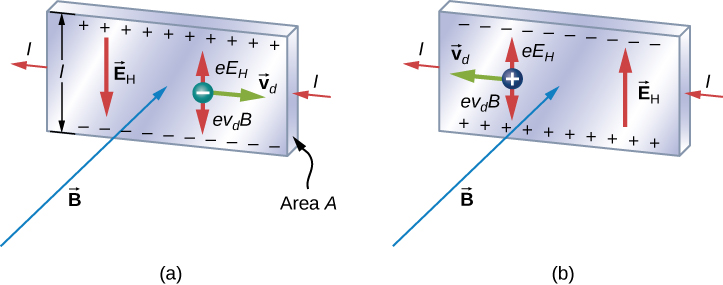
Een scenario waarin de elektrische en magnetische velden loodrecht op elkaar staan, wordt een gekruiste-veldsituatie genoemd. Als deze velden gelijke en tegengestelde krachten op een geladen deeltje produceren met de snelheid die de krachten evenaart, kunnen deze deeltjes door een apparaat gaan, dat een snelheidskeuzeschakelaar wordt genoemd, onverbogen. Deze snelheid wordt vertegenwoordigd in vergelijking ref{11.26}. Om het even welke andere snelheid van een geladen deeltje dat in de zelfde gebieden wordt verzonden zou door de magnetische kracht of de elektrische kracht worden afgebogen.
terugkerend naar het Hall-effect, als de stroom in de strook I is, dan van Stroom en Weerstand, weten wij dat
waarbij n het aantal ladingsdragers per volume is en A de dwarsdoorsnede van de strook is. Door de vergelijkingen voor \(v_d\) en I te combineren ontstaat
Het veld E is gerelateerd aan het potentiaalverschil V tussen de randen van de strook door
De grootheid \(V\) heet de Hall-potentiaal en kan gemeten worden met een voltmeter. Als we ten slotte de vergelijkingen voor I en E combineren, krijgen we
waarbij de bovenrand van de strook in figuur (\PageIndex{1}) positief is ten opzichte van de onderrand.
We kunnen ook vergelijking \ref{11.24} en vergelijking \ref{11.28} combineren om een uitdrukking te krijgen voor de Hall-spanning in termen van het magneetveld:
Wat als de ladingsdragers positief zijn, zoals in figuur \(\PageIndex{1}\)? Voor dezelfde stroom I is de grootte van V nog steeds gegeven door vergelijking \ref{hallV}. De bovenrand is nu echter negatief ten opzichte van de onderrand. Door eenvoudig het teken van V te meten, kunnen we dus het teken van de meerderheid van de ladingsdragers in een metaal bepalen.
Hall potentiaalmetingen laten zien dat elektronen de dominante ladingsdragers zijn in de meeste metalen. De Hall-potentialen geven echter aan dat bij enkele metalen, zoals wolfraam, beryllium en veel halfgeleiders, de meerderheid van de ladingsdragers positief is. Het blijkt dat geleiding door positieve lading wordt veroorzaakt door de migratie van ontbrekende elektronplaatsen (gaten genoemd) op ionen. Geleidingen door gaten worden later bestudeerd in Condensed Matter Physics.
Het Hall-effect kan worden gebruikt om magnetische velden te meten. Als een materiaal met een bekende dichtheid van ladingsdragers n in een magnetisch veld wordt geplaatst en V wordt gemeten, dan kan het veld worden bepaald uit Vergelijking \ref{11.29}. In onderzoekslaboratoria waar de velden van elektromagneten die voor nauwkeurige metingen worden gebruikt zeer constant moeten zijn, wordt vaak een “Hall probe” gebruikt als onderdeel van een elektronische schakeling die het veld regelt.
voorbeeld \PageIndex{1}\): Velocity Selector
Een elektronenbundel komt een crossed-field velocity selector binnen met magnetische en elektrische velden van respectievelijk 2,0 mT en \(6,0 \ maal 10^3 \, N/C\). (a) Hoe groot moet de snelheid van de elektronenbundel zijn om de gekruiste velden zonder afbuiging te doorkruisen? Als het elektrisch veld wordt uitgeschakeld, (b) wat is dan de versnelling van de elektronenstraal en (c) wat is dan de straal van de cirkelbeweging die het gevolg is?
Strategie
De elektronenstraal wordt door geen van beide magnetische of elektrische velden afgebogen als deze krachten in evenwicht zijn. Op basis van deze gebalanceerde krachten berekenen we de snelheid van de bundel. Zonder het elektrische veld wordt alleen de magnetische kracht gebruikt in de tweede wet van Newton om de versnelling te vinden. Tenslotte wordt de straal van het pad gebaseerd op de resulterende cirkelbeweging van de magnetische kracht.
Oplossing
- De snelheid van de ongestoorde bundel elektronen met gekruiste velden wordt berekend met vergelijking \ref{11.25}:
- De versnelling wordt berekend uit de netto kracht van het magnetisch veld, gelijk aan massa maal versnelling. De grootte van de versnelling is:
- De straal van het pad komt uit een evenwicht van de cirkelvormige en magnetische krachten, of Vergelijking \ref{11.25}: \
Betekenis
Als de elektronen in de bundel snelheden zouden hebben boven of onder het antwoord in deel (a), dan zouden die elektronen een sterkere netto kracht ondervinden uitgeoefend door ofwel het magnetische ofwel het elektrische veld. Daarom zouden alleen de elektronen met deze specifieke snelheid het halen.
De Hall Potentiaal in een Zilverlint
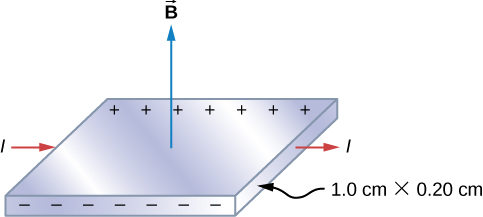
Figuur (PaginaIndex{2}) toont een zilverlint waarvan de doorsnede 1,0 cm bij 0,20 cm is. Het lint draagt van links naar rechts een stroom van 100 A, en het ligt in een uniform magneetveld van magnitude 1,5 T. Gebruik makend van een dichtheidswaarde van n = 5,9 maal 10^{28}) elektronen per kubieke meter voor zilver, bepaal dan de Hall-potentiaal tussen de randen van het lint.
Strategie
Omdat de meerderheid van de ladingsdragers elektronen zijn, is de polariteit van de Hall-spanning die welke in de figuur is aangegeven. De waarde van de Hall-spanning wordt berekend met behulp van vergelijking
Oplossing
Bij het berekenen van de Hall-spanning moeten we de stroom door het materiaal, het magnetisch veld, de lengte, het aantal ladingsdragers, en de oppervlakte weten. Omdat deze allemaal gegeven zijn, wordt de Hall-spanning berekend als:
&= \frac{(100 \, A)(1.5, T)(1,0 maal 10^{-2}m)}{(5,9 maal 10^{28} /m^3)(1,6 maal 10^{-19}C)(2,0 maal 10^{-5}m^2)} &= 7.9 \times 10^{-6}V.
Einde{align*}
Betekenis
Zoals in dit voorbeeld, is de Hall-potentiaal over het algemeen zeer klein, en zorgvuldig experimenteren met gevoelige apparatuur is vereist voor de meting ervan.
PageIndex{1})
Een Hall-sonde bestaat uit een koperstrip, n = 8,5 keer 10^{28}) elektronen per kubieke meter, die 2,0 cm breed en 0,10 cm dik is. Wat is het magnetisch veld als I = 50 A en de Hall-potentiaal
- (4,0 T, \mu V\) en
- (6,0 T, \mu V\)?
Antwoord a
1,1 T
Antwoord b
1.6 T
Bijdragers en toeschrijvingen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), en Bill Moebs met vele auteurs die een bijdrage hebben geleverd. Dit werk is gelicenseerd door OpenStax University Physics onder een Creative Commons Naamsvermelding Licentie (by 4.0).