Hypothesetoetsing en betrouwbaarheidsintervalEdit
De p-waarde voor kappa wordt zelden gerapporteerd, waarschijnlijk omdat zelfs betrekkelijk lage kappa-waarden toch significant van nul kunnen verschillen, maar niet groot genoeg zijn om onderzoekers tevreden te stellen.
Er kunnen betrouwbaarheidsintervallen voor kappa worden berekend, voor de verwachte kappa-waarden als we een oneindig aantal items zouden controleren, met de volgende formule:
C I : κ ± Z 1 – α / 2 S E κ {\displaystyle CI:\kappa \pm Z_{1-\alpha /2}SE_{\kappa }}

Waar Z 1 – α / 2 = 1,965 {{displaystyle Z_{1-alfa /2}=1,965}

is het standaard normale percentiel wanneer α = 5% {Displaystyle \alpha =5%}

, en S E κ = p o ( 1 – p o ) N ( 1 – p e ) 2 {\displaystyle SE_{\kappa }={\sqrt {{p_{o}(1-p_{o})} \over {N(1-p_{e})^{2}}}}}

Dit wordt berekend door te negeren dat pe wordt geschat op basis van de gegevens, en door po te behandelen als een geschatte kans van een binomiale verdeling terwijl gebruik wordt gemaakt van asymptotische normaliteit (d.w.z.: ervan uitgaande dat het aantal items groot is en dat po niet dicht bij hetzij 0 hetzij 1 ligt). S E κ {{{{} SE_{}}

(en de CI in het algemeen) kunnen ook worden geschat met bootstrapmethoden.
Interpretatie van magnitudeEdit

Als statistische significantie geen bruikbare leidraad is, welke grootte van kappa weerspiegelt dan adequate overeenstemming? Richtlijnen zouden nuttig zijn, maar andere factoren dan overeenkomst kunnen de grootte beïnvloeden, wat de interpretatie van een gegeven grootte problematisch maakt. Zoals Sim en Wright opmerkten, zijn twee belangrijke factoren prevalentie (zijn de codes equiprobeerbaar of variëren hun waarschijnlijkheden) en bias (zijn de marginale waarschijnlijkheden voor de twee waarnemers gelijk of verschillend). Als alle andere factoren gelijk zijn, zijn de kappa’s hoger wanneer de codes equiprobabel zijn. Anderzijds zijn de kappa’s hoger wanneer de codes asymmetrisch verdeeld zijn over de twee waarnemers. In tegenstelling tot waarschijnlijkheidsvariaties is het effect van bias groter wanneer de Kappa klein is dan wanneer hij groot is.:261-262
Een andere factor is het aantal codes. Naarmate het aantal codes toeneemt, worden de kappa’s groter. Op basis van een simulatiestudie concludeerden Bakeman en collega’s dat voor feilbare waarnemers de waarden voor kappa lager waren wanneer er minder codes waren. En, in overeenstemming met de verklaring van Sim & Wrights betreffende prevalentie, waren kappa’s hoger wanneer codes ruwweg equiprobabel waren. Bakeman et al. concludeerden dus dat “geen enkele waarde van kappa als universeel aanvaardbaar kan worden beschouwd.”:357 Zij bieden ook een computerprogramma aan waarmee gebruikers waarden voor kappa kunnen berekenen, waarbij ze het aantal codes, hun waarschijnlijkheid en de nauwkeurigheid van de waarnemer specificeren. Bijvoorbeeld, gegeven equiprobable codes en waarnemers die 85% accuraat zijn, zijn de waarden van kappa 0.49, 0.60, 0.66, en 0.69 wanneer het aantal codes respectievelijk 2, 3, 5, en 10 is.
Niettemin zijn er in de literatuur magnitude-richtlijnen verschenen. Misschien de eerste was Landis en Koch, die waarden < 0 gekenmerkt als indicatie geen overeenstemming en 0-0,20 als licht, 0,21-0,40 als redelijk, 0,41-0,60 als matig, 0,61-0,80 als substantieel, en 0,81-1 als bijna perfecte overeenstemming. Deze richtlijnen zijn echter geenszins universeel aanvaard; Landis en Koch hebben geen bewijs geleverd om ze te ondersteunen, maar baseren zich in plaats daarvan op persoonlijke opinie. Er is opgemerkt dat deze richtlijnen eerder schadelijk dan nuttig kunnen zijn. Fleiss’s:218 even arbitraire richtlijnen karakteriseren kappas boven 0.75 als uitstekend, 0.40 tot 0.75 als redelijk tot goed, en onder 0.40 als slecht.
Kappa maximumEdit
Kappa bereikt zijn theoretische maximumwaarde van 1 alleen als beide waarnemers codes hetzelfde verdelen, dat wil zeggen, als de corresponderende rij- en kolom-sommen identiek zijn. Alles minder is minder dan perfecte overeenstemming. Toch helpt de maximumwaarde die kappa zou kunnen bereiken bij ongelijke verdelingen om de werkelijk verkregen waarde van kappa te interpreteren. De vergelijking voor κ maximum is:
κ max = P max – P exp 1 – P exp {{\kappa _{\max }={\frac {P_{\max }-P_{\exp }}{1-P_{\exp }}}}

waar P exp = ∑ i = 1 k P i + P + i {\displaystyle P_{\exp }==\sum _{i=1}^{k}P_{i+}P_{+i}}

, zoals gebruikelijk, P max = ∑ i = 1 k min ( P i + , P + i ) {\displaystyle P_{\max }=\sum _{i=1}^{k}\min(P_{i+},P_{+i})}

,
k = aantal codes, P i + {{\displaystyle P_{i+}}

zijn de rijenwaarschijnlijkheden, en P + i {\displaystyle P_{+i}}

zijn de kolomwaarschijnlijkheden.
BeperkingenEdit
Kappa is een index die waargenomen overeenstemming beschouwt ten opzichte van een basislijnovereenkomst. Onderzoekers moeten echter zorgvuldig nagaan of Kappa’s baseline overeenkomst relevant is voor de specifieke onderzoeksvraag. Kappa’s baseline wordt vaak beschreven als de overeenkomst als gevolg van toeval, wat slechts gedeeltelijk juist is. Kappa’s basislijn overeenkomst is de overeenkomst die zou worden verwacht als gevolg van willekeurige toewijzing, gegeven de hoeveelheden die zijn gespecificeerd door de marginale totalen van de vierkante contingentietabel. Dus, Kappa = 0 wanneer de waargenomen toewijzing schijnbaar willekeurig is, ongeacht de hoeveelheid onenigheid zoals beperkt door de marginale totalen. Voor veel toepassingen zouden onderzoekers echter meer geïnteresseerd moeten zijn in het hoeveelheidsverschil in de marginale totalen dan in het allocatieverschil zoals beschreven door de extra informatie op de diagonaal van de vierkante contingentietabel. Voor veel toepassingen is de basislijn van Kappa dus eerder afleidend dan verhelderend. Neem het volgende voorbeeld:
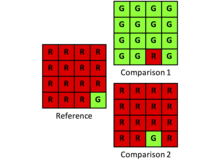
| Reference | |||
|---|---|---|---|
| G | R | ||
| Vergelijking | G | 1 | 14 |
| R | 0 | 1 | |
Het aandeel onenigheid is 14/16 of 0.875. De onenigheid is te wijten aan de hoeveelheid omdat de toewijzing optimaal is. Kappa is 0,01.
| Reference | |||
|---|---|---|---|
| G | R | ||
| Vergelijking | G | 0 | 1 |
| R | 1 | 14 | |
De onenigheidverhouding is 2/16 of 0.125. Het verschil is te wijten aan de toewijzing omdat de hoeveelheden identiek zijn. Kappa is -0,07.
Hier is het rapporteren van hoeveelheid- en allocatieafwijkingen informatief, terwijl Kappa informatie versluiert. Bovendien brengt Kappa enige problemen met zich mee bij de berekening en interpretatie, omdat Kappa een verhouding is. Het is mogelijk dat de Kappa-verhouding een ongedefinieerde waarde oplevert door nul in de noemer. Bovendien geeft een ratio noch de teller, noch de noemer prijs. Het is informatiever voor onderzoekers om onenigheid te rapporteren in twee componenten, kwantiteit en allocatie. Deze twee componenten beschrijven de relatie tussen de categorieën duidelijker dan een enkele samenvattende statistiek. Wanneer voorspellende nauwkeurigheid het doel is, kunnen onderzoekers gemakkelijker beginnen na te denken over manieren om een voorspelling te verbeteren door twee componenten van hoeveelheid en toewijzing te gebruiken, in plaats van één ratio van Kappa.
Sommige onderzoekers hebben hun bezorgdheid geuit over κ’s neiging om de waargenomen categoriefrequenties als gegeven te nemen, wat het onbetrouwbaar kan maken voor het meten van overeenkomst in situaties zoals de diagnose van zeldzame ziekten. In deze situaties heeft κ de neiging de overeenstemming over de zeldzame categorie te onderschatten. Om deze reden wordt κ beschouwd als een te conservatieve maat van overeenkomst. Anderen betwisten de bewering dat kappa “rekening houdt met” toevallige overeenstemming. Om dit effectief te doen zou een expliciet model nodig zijn van hoe toeval beslissingen van beoordelaars beïnvloedt. De zogenaamde toevalscorrectie van de kappastatistiek veronderstelt dat beoordelaars, wanneer ze niet helemaal zeker zijn, gewoon gissen – een zeer onrealistisch scenario.