In onze vorige les hebben we bestudeerd hoe we de regel van Cramer kunnen gebruiken met twee variabelen. Ons doel hier is om de toepassing van de regel van Cramer uit te breiden naar drie variabelen, meestal in termen van \groot{x}, \groot{y}, en \groot{z}. Ik zal vijf (5) uitgewerkte voorbeelden bespreken om je met dit concept vertrouwd te maken.
Om dit onderwerp goed te doen, moet je een idee hebben hoe je de determinant van een 3⨉3 matrix vindt. Dat is dus wat we eerst gaan doen. Klaar?
Formule om de determinant van een 3⨉3 matrix te vinden
- Geef een 3⨉3 matrix

- De determinant kan worden berekend met de volgende formule.
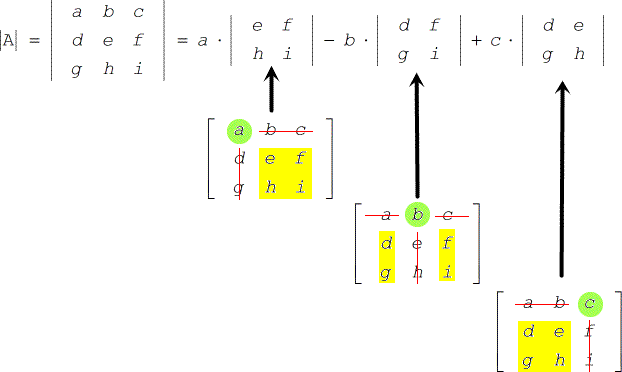
Laten we hier eens een snel voorbeeld van doen.
Vind de determinant van matrix A
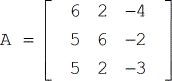
Oplossing: Zorg ervoor dat je de formule over hoe je de determinant van een 3×3 matrix vindt zorgvuldig volgt, zoals hierboven is aangegeven. Meer nog, haast je niet bij het uitvoeren van de vereiste rekenkundige bewerkingen in elke stap. Dit is waar veel voorkomende fouten meestal optreden, maar het kan worden voorkomen. Als je het goed doet, moet je oplossing lijken op die hieronder.
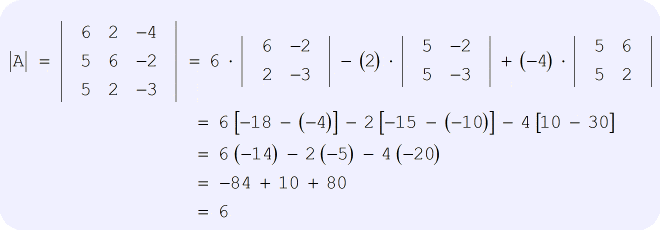
Nu is het tijd om de procedure door te nemen voor het gebruik van de regel van Cramer in een lineair stelsel met drie variabelen.
Cramer’s Regels voor stelsels lineaire vergelijkingen met drie variabelen
- Gegeven een lineair stelsel

- Labeling van elk van de vier matrices
coëfficiëntenmatrix:
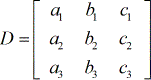
X – matrix:
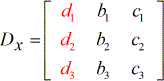
Y – matrix:
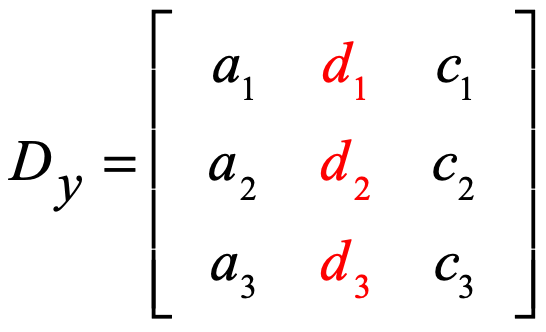
Z – matrix:
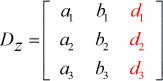
- Om voor x op te lossen:
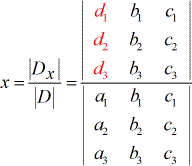
- Om voor y op te lossen:
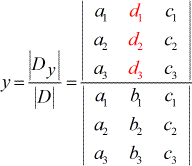
- Om voor z op te lossen:
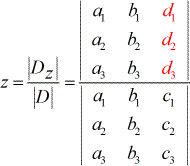
Dingen die je uit bovenstaande opzet kunt opmerken:
1) De coëfficiënten van de variabelen x, y, en z maken gebruik van respectievelijk subscripted a, b, en c. Terwijl de constante termen gebruik maken van subscripted d.
2) De noemers om de waarden van x, y, en z te vinden zijn allemaal hetzelfde en dat is de determinant van de coëfficiëntenmatrix (coëfficiënten afkomstig uit de kolommen van x, y, en z).
3) Om voor x op te lossen, worden de coëfficiënten van de x-kolom vervangen door de constante kolom (in rood).
4) Om voor y op te lossen, worden de coëfficiënten van de y-kolom vervangen door de constante kolom (in rood).
5) Op dezelfde manier worden, om voor z op te lossen, de coëfficiënten van de z-kolom vervangen door de constante kolom (in rood).
Voorbeelden van het oplossen van stelsels lineaire vergelijkingen met drie variabelen met behulp van de regel van Cramer
Voorbeeld 1: Los het stelsel met drie variabelen op met behulp van de regel van Cramer.
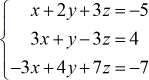
Van het gegeven stelsel van lineaire vergelijkingen, construeer ik de vier matrices die gebruikt zullen worden om de waarden van x, y en z op te lossen.
Gebruik bovenstaande handleiding om deze speciale matrices correct op te stellen.
- coëfficiëntenmatrix
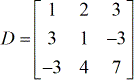
- X – matrix
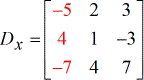
- Y – matrix
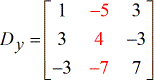
- Z – matrix
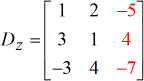
Volgende stap is het oplossen van de determinant van elke matrix. Om dit te doen, kan ik handmatig de determinant van elke matrix op papier oplossen met behulp van de bovenstaande formule. Het kan vervelend zijn, maar dat geeft niet, want goede wiskundevaardigheden ontwikkel je door veel problemen te maken.
De waarden van de determinanten staan hieronder vermeld.
Determinanten van elke matrix:
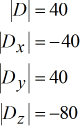
De uiteindelijke antwoorden of oplossingen zijn eenvoudig te berekenen of te berekenen als alle benodigde determinanten zijn gevonden.
De opgeloste waarden voor \groot{green}x}, \groot{green}y}, en \groot{green}z}.
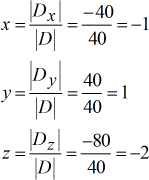
Het uiteindelijke antwoord geschreven in puntnotatie is links( {x,y,z} rechts) = links( { – 1,1, – 2} rechts).
Voorbeeld 2: Los het stelsel met drie variabelen op met de regel van Cramer.
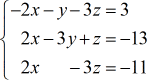
Ik beschouw de coëfficiëntenmatrix eigenlijk als de “primaire” matrix, omdat de andere drie matrices ervan zijn afgeleid. De x-matrix is bijvoorbeeld gewoon de “primaire” matrix met de x-kolom vervangen door de constante kolom (in rood). U ziet dat hetzelfde patroon wordt toegepast bij het construeren van de andere matrices: y en z.
- coëfficiëntenmatrix
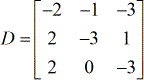
- X – matrix
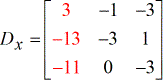
- Y – matrix
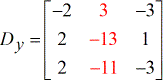
- Z – matrix
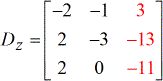
Na het oplossen van de determinant van elke matrix, heb ik ze allemaal opgeschreven.
Determinanten van elke matrix:
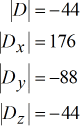
De waarden voor x, y en z worden als volgt berekend. Merk op dat x wordt verkregen door de determinant van de x-matrix te delen door de determinant van de coëfficiëntenmatrix. Deze regel geldt ook voor de rest.
Oplossingen voor de waarden van x, y en z.
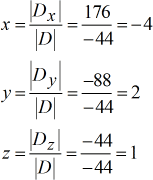
Het uiteindelijke antwoord is links( {x,y,z} rechts) = links( { – 4,2,1} rechts).
Voorbeeld 3: Los het stelsel met drie variabelen op met de regel van Cramer.
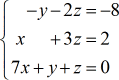
Dit probleem is veel eenvoudiger dan de eerste twee voorbeelden door de aanwezigheid van nulpunten in de kolommen x, y, en constante. Ziet u het? Wanneer we nul ingangen in een matrix hebben, wordt de berekening van de determinant dramatisch vereenvoudigd.
In feite, naarmate je het aantal nullen in een vierkante matrix verhoogt, wordt het werk dat je moet doen om de determinant te vinden sterk verminderd.
Hier zijn de matrices uit het stelsel van lineaire vergelijkingen.
- coëfficiëntenmatrix
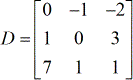
- X – matrix
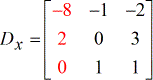
- Y – matrix
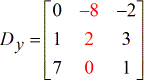
- Z – matrix
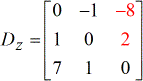
Oplossend voor hun determinanten, kreeg ik de volgende waarden.
Determinanten van elke matrix:
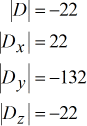
Dit leidt ons tot het eenvoudig opstellen en berekenen van de eindantwoorden.
De opgeloste waarden voor \groot{green}x}, en \groot{green}y}, en \groot{green}z}.
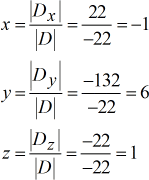
Het uiteindelijke antwoord is links( {x,y,z} rechts) = links( { – \,1,6,1} rechts).
Voorbeeld 4: Het stelsel met drie variabelen oplossen met de regel van Cramer
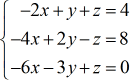
Opschrijven van de vier speciale matrices.
- coëfficiëntenmatrix
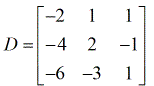
- X – matrix
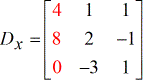
- Y – matrix
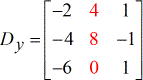
- Z – matrix
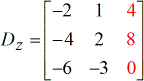
Evalueer elke matrix om de determinant ervan te vinden.
Dit zijn de determinanten van elke matrix:
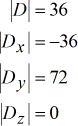
Gebruik de regel van Cramer om de volgende oplossingen te krijgen.
Oplossingswaarden voor \groot{groen}x}, \groot{groen}y}, en \groot{groen}z}.
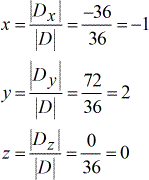
Het uiteindelijke antwoord is links( {x,y,z} rechts) = links( { – \,1,2,0} rechts).
Voorbeeld 5: Los het stelsel met drie variabelen op met de regel van Cramer
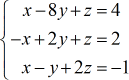
Laten we nog een laatste voorbeeld doen! Ik hoop dat je nu genoeg oefening hebt gehad in het oplossen van stelsels met drie variabelen met behulp van de regel van Cramer.
Ik stel voor dat je dit eerst op papier oplost en dan terugkomt om je antwoord te vergelijken. Maak je geen zorgen, niemand kijkt mee. 👀 Als je klaar bent, scroll je naar beneden om de oplossing te zien.

Bouw de vier speciale matrices.
- coëfficiëntenmatrix
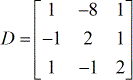
- X – matrix
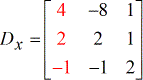
- Y – matrix
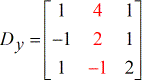
- Z – matrix
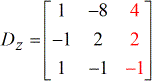
Vind de determinant van elke vierkante matrix.
Determinanten van elke matrix
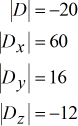
Oplos voor x, y en z met behulp van de gegeven formule.
Oplos voor \groot{groen}x}, \groot{groen}y}, en \groot{groen}z}.
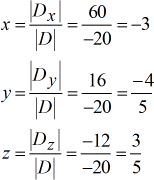
Doen! Het uiteindelijke antwoord in puntvorm is links( {x,y,z}} rechts) = {groot} links( { – \,3, – {4 \over 5},{3 \over 5}} rechts)}}.
Oefenen met werkbladen
Je bent misschien ook geïnteresseerd in:
Cramer’s Regel 2×2