Inleiding
Regressieanalyse wordt gewoonlijk gebruikt voor het modelleren van het verband tussen een enkele afhankelijke variabele Y en een of meer voorspellers. Wanneer we één voorspeller hebben, noemen we dit “eenvoudige” lineaire regressie:
E = β0 + β1X
Dat wil zeggen dat de verwachte waarde van Y een rechtlijnige functie is van X. De bèta’s worden gekozen door de lijn te kiezen die de gekwadrateerde afstand tussen elke Y-waarde en de best passende lijn zo klein mogelijk maakt. De bèta’s worden zo gekozen dat zij deze uitdrukking minimaliseren:
∑i (yi – (β0 + β1X))2
Een instructieve afbeelding die ik op het internet vond

Bron: http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Wanneer we meer dan één voorspeller hebben, spreken we van meervoudige lineaire regressie:
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
De gepaste waarden (d.w.z., de voorspelde waarden) zijn gedefinieerd als de waarden van Y die worden gegenereerd als we onze X-waarden in ons geteste model stoppen.
De residuen zijn de geteste waarden min de werkelijke waargenomen waarden van Y.
Hier volgt een voorbeeld van een lineaire regressie met twee voorspellers en één uitkomst:
In plaats van de “line of best fit,” is er een “plane of best fit.”
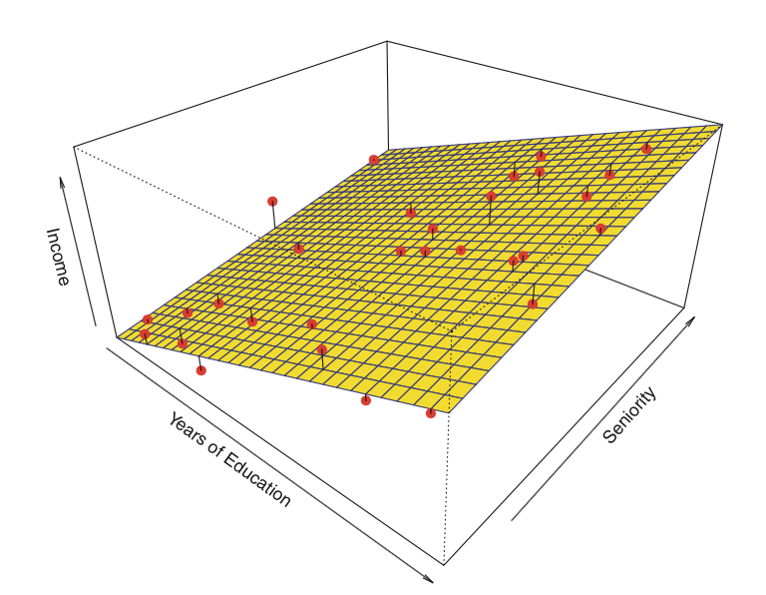
Bron: James et al. Introduction to Statistical Learning (Springer 2013)
Er zijn vier aannames verbonden aan een lineair regressiemodel:
- Lineariteit: Het verband tussen X en het gemiddelde van Y is lineair.
- Homoscedasticiteit: De variantie van het residu is gelijk voor elke waarde van X.
- Onafhankelijkheid: Waarnemingen zijn onafhankelijk van elkaar.
- Normaliteit: Voor elke vaste waarde van X is Y normaal verdeeld.
We zullen later in de module bekijken hoe we deze aannames kunnen beoordelen.
Laten we beginnen met eenvoudige regressie. In R worden modellen gewoonlijk ingepast door een model-fitting functie aan te roepen, in ons geval lm(), met een “formula” object dat het model beschrijft en een “data.frame” object dat de variabelen bevat die in de formule worden gebruikt. Een typische aanroep kan er als volgt uitzien
> myfunction <- lm(formule, data, …)
en het zal een gepast model object teruggeven, hier opgeslagen als myfunction. Dit aangepaste model kan vervolgens worden afgedrukt, samengevat of gevisualiseerd; bovendien kunnen de aangepaste waarden en residuen worden geëxtraheerd, en kunnen we voorspellingen doen op nieuwe gegevens (waarden van X), berekend met functies als summary(), residuals(), predict(), enz. Hierna zullen we bekijken hoe we een eenvoudige lineaire regressie kunnen fitten.
terug naar boven | vorige pagina | volgende pagina