Basisprincipes van Grafieken Exponentiële functies
De exponentiële functie y=b^x waarbij b>0 is een functie die evenredig blijft met haar oorspronkelijke waarde wanneer zij groeit of afneemt.
Leerdoelen
Beschrijf de eigenschappen van grafieken van exponentiële functies
Key Takeaways
Key Points
- Als de basis, b, groter is dan 1, dan neemt de functie exponentieel toe met een groeisnelheid van b. Dit staat bekend als exponentiële groei.
- Als het grondtal b kleiner is dan 1 (maar groter dan 0) neemt de functie exponentieel af met een snelheid van b. Dit staat bekend als exponentieel verval.
- Als het grondtal b gelijk is aan 1, dan wordt de functie triviaal y=a.
- De punten (0,1) en (1,b) liggen altijd op de grafiek van de functie y=b^x
- De functie y=b^x neemt alleen positieve waarden aan en heeft de x-as als horizontale asymptoot.
Key Terms
- exponentiële groei: De groei van de waarde van een grootheid, waarbij de groeisnelheid evenredig is met de momentane waarde van de grootheid; bijvoorbeeld, wanneer de waarde is verdubbeld, zal de groeisnelheid ook zijn verdubbeld. Het tempo kan positief of negatief zijn. Als het negatief is, wordt het ook exponentieel verval genoemd.
- asymptoot: Een lijn die een kromme willekeurig dicht nadert. Een asymptoot kan verticaal, schuin of horizontaal zijn. Horizontale asymptoten komen overeen met de waarde die de kromme nadert als x zeer groot of zeer klein wordt.
- exponentiële functie: Elke functie waarin een onafhankelijke variabele in de vorm van een exponent voorkomt; het zijn de inverse functies van logaritmen.
Definities
Op het meest basale niveau is een exponentiële functie een functie waarin de variabele in de exponent voorkomt. De meest elementaire exponentiële functie is een functie van de vorm y=b^x waarbij b een positief getal is.
Wanneer b>1 groeit de functie op een manier die evenredig is met de oorspronkelijke waarde. Dit heet exponentiële groei.
Wanneer 0>b>1 neemt de functie af op een manier die evenredig is met haar oorspronkelijke waarde. Dit heet exponentieel verval.
Grafiek van een exponentiële functie
Laten we eens kijken naar de functie y=2^x als b>1. Een manier om deze functie grafisch weer te geven is door waarden voor x te kiezen en deze in de vergelijking te substitueren om waarden voor y te genereren. Dit levert de volgende punten op:
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) en (2,4)
Als je de punten met elkaar verbindt, zie je een vloeiende kromme die de y-as kruist in het punt (0,1) en steeds groter wordt naarmate x een steeds grotere waarde aanneemt. Dat wil zeggen dat de kromme oneindig wordt naarmate x oneindig wordt. Als x steeds kleiner wordt, komt de kromme steeds dichter bij de x-as te liggen. Dat wil zeggen dat de kromme nul nadert als x negatief oneindig nadert, waardoor de x-as een horizontale asymptoot van de functie is. Het punt (1,b) ligt op de grafiek. Dit geldt voor de grafiek van alle exponentiële functies van de vorm y=b^x voor x>1.

Grafiek van y=2^x: De grafiek van deze functie snijdt de y-as bij (0,1) en neemt toe naarmate x het oneindige nadert. De x-as is een horizontale asymptoot van de functie.
Voorbeeld 2
Beschouwen we de functie y=2^x als 0<b<1. Een manier om deze functie grafisch weer te geven is door waarden voor x te kiezen en deze in de vergelijking te substitueren om waarden voor y te genereren. Zo krijg je de volgende punten:
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) en (2,\frac{1}{4})
Als je de punten met elkaar verbindt zie je een vloeiende kromme die de y-as kruist in het punt (0,1) en afneemt naarmate x steeds grotere waarden aanneemt. De kromme nadert oneindig nul als oneindig nadert. Als x steeds kleiner wordt, komt de kromme steeds dichter bij de x-as te liggen. Dat wil zeggen, de kromme nadert nul als x negatief oneindig nadert, waardoor de x-as een horizontale asymptoot van de functie wordt. Het punt (1,b) ligt op de grafiek. Dit geldt voor de grafiek van alle exponentiële functies van de vorm y=b^x voor 0<x<1.
Zoals je in de grafiek hieronder kunt zien, is de grafiek van y=\frac{1}{2}^x symmetrisch met die van y=2^x over de y-as. Dat wil zeggen dat als het vlak over de y-as zou worden gevouwen, de twee krommen op elkaar zouden liggen.
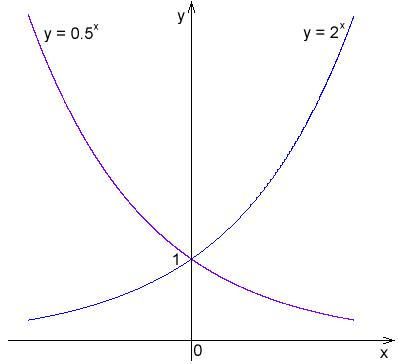
Grafiek van y=2^x en y=\frac{1}{2}^x: De grafieken van deze functies zijn symmetrisch over de y-as.
Waarom moet b een positief getal zijn?
Als b=1, dan wordt de functie y=1^x. Aangezien 1 tot elke macht 1 oplevert, is de functie gelijk aan y=1, wat een horizontale lijn is, geen exponentiële vergelijking.
Als b negatief is, dan resulteert verhoging van b tot een even macht in een positieve waarde voor y, terwijl verhoging van b tot een oneven macht resulteert in een negatieve waarde voor y, waardoor het onmogelijk is de verkregen punten op een zinvolle manier samen te voegen en zeker niet op een manier die een kromme oplevert zoals in de voorbeelden hierboven.
Eigenschappen van exponentiële grafieken
Het punt (0,1) ligt altijd op de grafiek van een exponentiële functie van de vorm y=b^x omdat b positief is en elk positief getal tot de macht nul levert 1 op.
Het punt (1,b) ligt altijd op de grafiek van een exponentiële functie van de vorm y=b^x omdat elk positief getal b tot de eerste macht 1 oplevert.
De functie y=b^x neemt alleen positieve waarden aan omdat elk positief getal b alleen positieve waarden oplevert als het tot een willekeurige macht wordt verheven.
De functie y=b^x heeft de x-as als horizontale asymptoot omdat de kromme altijd de x-as zal naderen als x ofwel positief ofwel negatief oneindig nadert, maar nooit de as zal kruisen omdat deze nooit gelijk aan nul zal zijn.
Grafieken van logaritmische functies
Logaritmische functies kunnen handmatig of elektronisch worden gegraveerd, waarbij de punten meestal met behulp van een rekenmachine of tabel worden bepaald.
Leerdoelen
Beschrijf de eigenschappen van grafieken van logaritmische functies
Key Takeaways
Key Points
- In een grafiek lijkt de logaritmische functie op de vierkantswortelfunctie, maar dan met een verticale asymptoot als x van rechts naar 0 nadert.
- Het punt (1,0) ligt op de grafiek van alle logaritmische functies van de vorm y=log{_b}x, waarbij b een positief reeel getal is.
- Het domein van de logaritmische functie y=log{_b}x, waarbij b alle positieve reële getallen zijn, is de verzameling van alle positieve reële getallen, terwijl het bereik van deze functie alle reële getallen is.
- De grafiek van een logaritmische functie van de vorm y=log{_b}x kan horizontaal en/of verticaal verschoven worden door een constante toe te voegen aan respectievelijk de variabele x of aan y.
- Een logaritmische functie van de vorm y=log{_b}x waarbij b een positief reëel getal is, kan grafisch worden weergegeven door met een rekenmachine punten op de grafiek te bepalen of kan zonder rekenmachine grafisch worden weergegeven door gebruik te maken van het feit dat de inverse een exponentiële functie is.
Key Terms
- logaritmische functie: Elke functie waarin een onafhankelijke variabele voorkomt in de vorm van een logaritme. De inverse van een logaritmische functie is een exponentiële functie en vice versa.
- logaritme: De logaritme van een getal is de exponent waarmee een andere vaste waarde, de basis, moet worden verhoogd om dat getal te produceren.
- asymptoot: Een lijn die een kromme willekeurig dicht nadert. Asymptoten kunnen horizontaal, verticaal of schuin zijn.
Hieronder staan grafieken van logaritmische functies met grondslagen 2, e, en 10.
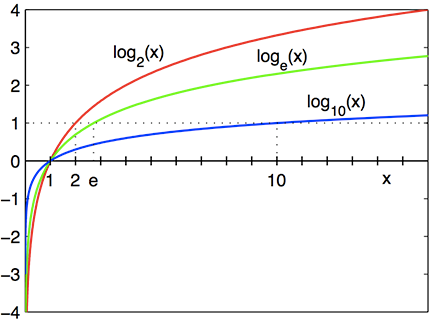
Logaritmische grafieken: Na x=1, waar de grafieken de x-as kruisen, staat \log_2(x) in het rood boven \log_e(x) in het groen, die boven \log_{10}(x) in het blauw staat. Voor dit punt is de volgorde omgekeerd. Alle drie de logaritmen hebben de y-as als verticale asymptoot, en zijn altijd stijgend.
Alledrie de logaritmische grafieken beginnen met een steile klim na x=0, maar strekken zich steeds meer horizontaal uit, waarbij hun helling steeds kleiner wordt naarmate x toeneemt. Ze kruisen allemaal de x-as bij x=1.
Eigenschappen van de grafieken van logaritmische functies
De grafiek kruist de x-as bij 1. Dat wil zeggen, de grafiek heeft een x-afsnijpunt van 1, en als zodanig ligt het punt (1,0) op de grafiek. In feite ligt het punt (1,0) altijd op de grafiek van een functie van de vorm y=log{_b}x waarbij b>0. Voor x=1 wordt de vergelijking van de grafiek namelijk y=log{_b}1.
Dus zijn we op zoek naar een exponent y zodat b^y=1. Aangezien b>0 is, is de exponent die we zoeken 1, ongeacht de waarde van b. Dit betekent dat het punt (x,y)=(1,0) altijd op een logaritmische functie van dit type zal liggen.
Asymptoten
De y-as is een verticale asymptoot van de grafiek. Dit betekent dat de kromme steeds dichter bij de y-as komt, maar deze niet kruist.
Laten we eens kijken wat er gebeurt als de waarde van x van rechts nul nadert voor de vergelijking waarvan de grafiek hierboven staat. Namelijk, y=log{_b}x. We kunnen dit doen door waarden voor x te kiezen, die in de vergelijking in te vullen en zo waarden voor y te genereren.
Laten we aannemen dat b een positief getal groter dan 1 is, en laten we waarden van x tussen 0 en 1 onderzoeken. Onder deze omstandigheden wordt de vergelijking, als we x==Log = b.
Dus zoeken we een exponent zodanig dat b verheven tot die exponent resulteert in γfrac{1}{b}. De exponent die we zoeken is -1 en het punt (\frac{1}{b},-1) ligt op de grafiek. Op dezelfde manier kunnen we de volgende punten krijgen die ook op de grafiek liggen:
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) enzovoort
Als we waarden van x nemen die nog dichter bij 0 liggen, komen we op de volgende punten uit: (\frac{1}{b^{10}},-10),(\frac{1}{b^{100}},-100) en (\frac{1}{b^{1000}},-1000)
Zoals je ziet wordt de grafiek steeds negatiever naarmate de waarde van x dichter bij 0 komt. Dat wil zeggen, als x dichter bij nul komt, nadert de grafiek negatieve oneindigheid. Dit betekent dat de y-as een verticale asymptoot van de functie is.
Domein en Bereik
Het domein van de functie bestaat uit alle positieve getallen. Dat betekent dat de x-waarde van de functie altijd positief zal zijn. Laten we eerst eens nagaan waarom de x-waarde van de kromme nooit 0 is.
Als de x-waarde nul zou zijn, zou de functie luiden y=log{_b}0.
Hier zoeken we een exponent zodanig dat b verheven tot die exponent 0 is. Aangezien b een positief getal is, is er geen exponent waartoe we b kunnen verheffen om 0 te krijgen. In feite, aangezien b positief is, zal verheffen tot een macht altijd een positief getal opleveren.
Het bereik van de functie is alle reële getallen. Dat wil zeggen dat de grafiek elk reëel getal kan aannemen.
Vergelijking van y=log{_x} en y=\sqrt{x}
Op het eerste gezicht kan de grafiek van de logaritmische functie gemakkelijk verward worden met die van de vierkantswortel functie.
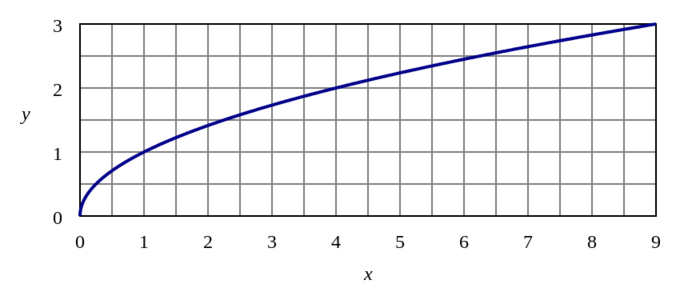
Grafiek van y=\sqrt{x}: De grafiek van de vierkantswortelfunctie lijkt op de grafiek van de logaritmische functie, maar heeft geen verticale asymptoot.
Zowel de vierkantswortel- als de logaritmische functie hebben een domein dat beperkt is tot x-waarden groter dan 0. De logaritmische functie heeft echter een verticale asymptoot die afdaalt naar -40 naarmate x dichter bij 0 komt, terwijl de vierkantswortel een minimale y-waarde van 0 bereikt. Het bereik van de vierkantswortelfunctie is alle niet-negatieve reële getallen, terwijl het bereik van de logaritmische functie alle reële getallen is.
Grafiek van logaritmische functies
Grafiek van logaritmische functies kan worden gedaan door punten op de kromme met de hand of met een rekenmachine te zoeken.
Bij grafiektekenen zonder rekenmachine gebruiken we het feit dat de inverse van een logaritmische functie een exponentiële functie is.
Bij grafieken met een rekenmachine maken we gebruik van het feit dat de rekenmachine alleen gewone logaritmen (basis is 10), natuurlijke logaritmen (basis is e) of binaire logaritmen (basis is 2) kan berekenen. Natuurlijk, als we een grafische rekenmachine hebben, kan de rekenmachine een grafiek van de functie maken zonder dat we punten op de grafiek hoeven te vinden.
Grafiek van logaritmische functies met behulp van hun inverses
Logaritmische functies kunnen met de hand worden berekend zonder gebruik te maken van een rekenmachine, als we gebruik maken van het feit dat ze inverses zijn van exponentiële functies.
Laten we opnieuw de grafiek van de volgende functie bekijken:
y=log{_3}x
Dit kan in exponentiële vorm worden geschreven als:
3^y=x
Nu bekijken we de inverse van deze functie. Daartoe verwisselen we x en y:
3^x=y
De exponentiële functie 3^x=y is er een waar we gemakkelijk punten voor kunnen genereren. Als we enkele waarden voor x nemen en die in de vergelijking stoppen om de overeenkomstige waarden voor y te vinden, krijgen we de volgende punten:
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) en (3,27)
Nou moeten we opmerken dat deze punten niet op de oorspronkelijke functie liggen (y=log{_3}x) maar eerder op zijn inverse 3^x=y. Als we echter de x- en y-coördinaten van elk punt omwisselen, krijgen we in feite een lijst van punten op de oorspronkelijke functie.
Dit zijn: (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) en (27,3).
We plotten en verbinden deze punten om de onderstaande grafiek van de functie y=log{_3}x te krijgen.

Grafiek van y=log{_3}x: De grafiek van de logaritmische functie met basis 3 kan worden gegenereerd met behulp van de inverse van de functie. De vorm is dezelfde als die van andere logaritmische functies, alleen met een andere schaal.
Grafiek van logaritmische functies met basen tussen 0 en 1
Tot nu toe hebben we een grafiek gemaakt van logaritmische functies waarvan de basen groter zijn dan 1. Als we in plaats daarvan logaritmische functies bekijken met een basis b, zodanig dat 0<b<1, dan krijgen we een grafiek die erg lijkt op de grafieken die we al gezien hebben.
In feite, als b>0 is, zijn de grafiek van y=log{_b}x en de grafiek van y=log{_frac{1}{b}}x symmetrisch over de x-as. Als we dus een punt (x,y) vinden op de grafiek van y=log{_b}x, dan kunnen we het overeenkomstige punt op y=log{_frac{1}{b}x vinden door het teken van de y-coördinaat te veranderen. Het overeenkomstige punt is (x,-y).
Hier volgt een voorbeeld voor b=2.
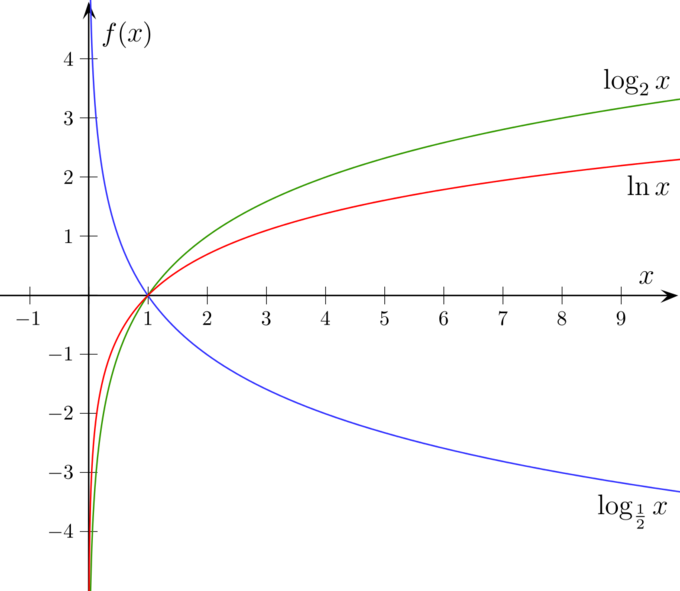
Grafieken van log{_2}x en log{_\frac{1}{2}}x : De grafieken van log_2 x en log{_\frac{1}{2}}x zijn symmetrisch over de x-as
Oplossen van problemen met logaritmische grafieken
Sommige functies met een snel veranderende vorm kunnen het beste worden uitgezet op een schaal die exponentieel toeneemt, zoals een logaritmische grafiek.
Leerdoelen
Omzetten van problemen naar logaritmische schalen en de voordelen daarvan bespreken
Key Takeaways
Key Points
- Logaritmische grafieken maken gebruik van logaritmische schalen, waarbij de waarden exponentieel verschillen. Bijvoorbeeld, in plaats van markeringen op 0,1,2 en 3, kan een logaritmische schaal markeringen op 0,1, 1, 10 en 100 bevatten, elk op gelijke afstand van de vorige en volgende.
- Logaritmische grafieken maken het mogelijk om een zeer groot bereik van gegevens te plotten zonder de vorm van de grafiek te verliezen.
- Logaritmische grafieken maken het gemakkelijker om te interpoleren in gebieden die moeilijk leesbaar zijn op lineaire assen. Bijvoorbeeld, als de plot y=x^5 is geschaald om een zeer breed bereik van y-waarden weer te geven, kan de kromming in de buurt van de oorsprong niet te onderscheiden zijn op lineaire assen. Op logaritmische assen is dat veel duidelijker.
Key Terms
- logaritme: De logaritme van een getal is de exponent waarmee een andere vaste waarde, de basis, moet worden verhoogd om dat getal te produceren.
- interpoleren: De waarde van een functie schatten tussen twee punten waartussen deze is getabelleerd.
Waarom een logaritmische schaal gebruiken?
Veel wiskundige en natuurkundige relaties zijn functioneel afhankelijk van variabelen van een hoge orde. Dit betekent dat voor kleine veranderingen in de onafhankelijke variabele er zeer grote veranderingen zijn in de afhankelijke variabele. Het wordt dus moeilijk om zulke functies op de standaardas in een grafiek weer te geven.
Bedenk als voorbeeld de wet van Stefan-Boltzmann, die het door een zwart lichaam uitgezonden vermogen (j*) relateert aan de temperatuur (T).
j^*= \sigma T^4
Op een standaardgrafiek kan deze vergelijking nogal onhandelbaar zijn. De vierdegraadsafhankelijkheid van de temperatuur betekent dat het vermogen extreem snel toeneemt. Het feit dat de snelheid steeds toeneemt (en steil) betekent dat het veranderen van schaal (schalen van de assen met 5, 10 of zelfs 100) weinig helpt om de grafiek gemakkelijker interpreteerbaar te maken.
Voor zeer steile functies is het mogelijk punten soepeler te plotten met behoud van de integriteit van de gegevens: men kan een grafiek gebruiken met een logaritmische schaal, waarbij in plaats van elke spatie op een grafiek een constante toename staat, deze een exponentiële toename voorstelt. Waar een normale (lineaire) grafiek gelijke intervallen heeft van 1, 2, 3, 4, stelt een logaritmische schaal diezelfde gelijke intervallen voor als 1, 10, 100, 1000. Hier zijn enkele voorbeelden van functies die zijn uitgezet op een lineaire schaal, een semi-logaritmische schaal en een logaritmische schaal.
Het bovenste links is een lineaire schaal. De schaal rechtsonder is een logaritmische schaal. Rechtsboven en linksonder worden semi-logische schalen genoemd omdat de ene as lineair wordt geschaald terwijl de andere met logaritmen wordt geschaald.

Logaritmische schaal: De grafieken van de functies f(x)=10^x,f(x)=x en f(x)=log x op vier verschillende coördinatenplots. Linksboven is een lineaire schaal, rechtsboven en linksonder zijn semi-logaritmische schalen en rechtsonder is een logaritmische schaal.
Zoals u kunt zien, heeft de grafiek bij gebruik van een logaritmische schaal voor beide assen (rechtsonder) de eigenschappen behouden van de oorspronkelijke grafiek (linksboven) waar voor beide assen een lineaire schaal werd gebruikt. Dat betekent dat als we een functie willen weergeven die onhandelbaar is op een lineaire schaal, we een logaritmische schaal op elke as kunnen gebruiken en de eigenschappen van de grafiek kunnen behouden, terwijl het tegelijkertijd gemakkelijker wordt om een grafiek te maken.
Met de semi-logische schalen hebben de functies vormen die scheefgetrokken zijn ten opzichte van het origineel. Wanneer alleen de x-as een log-schaal heeft, ziet de logaritmische curve er als een lijn uit en de lineaire en exponentiële curven beide als exponentieel. Wanneer alleen de y-as een log-schaal heeft, verschijnt de exponentiële kromme als een lijn en de lineaire en logaritmische krommen beide als logaritmisch.Opgemerkt moet worden dat de voorbeelden in de grafieken bedoeld waren om een punt te illustreren en dat de gegraveerde functies niet noodzakelijkerwijs onhandelbaar waren op een lineair geschaalde reeks assen.
Omzetting van lineaire naar logaritmische schalen
Het belangrijkste verschil tussen de logaritmische en lineaire schalen is dat, terwijl het verschil in waarde tussen lineaire punten van gelijke afstand constant blijft (dat wil zeggen, als de ruimte van 0 tot 1 op de schaal 1 cm is op de pagina, de afstand van 1 tot 2, 2 tot 3, enz, hetzelfde zijn), zal het verschil in waarde tussen punten op een logaritmische schaal exponentieel veranderen. Een logaritmische schaal begint bij een bepaalde macht van 10, en neemt met elke eenheid toe met een macht van 10.
Dus, als men een lineaire schaal (met waarden 0-5 naar een logaritmische schaal wil converteren, zou een optie zijn om 1,2,3,4 en 5 te vervangen door respectievelijk 0,001,0,01,0,1,1,10 en 100. Tussen elke hoofdwaarde op de logaritmische schaal komen de hashmarks steeds dichter bij elkaar te staan naarmate de waarde toeneemt. Bijvoorbeeld, in de ruimte tussen 1 en 10 staan de 8 en 9 veel dichter bij elkaar dan de 2 en 3.
Het gebruik van een logaritmische schaal heeft twee voordelen. Ten eerste kan men zo een zeer groot bereik van gegevens uitzetten zonder de vorm van de grafiek te verliezen. Ten tweede kan men op elk punt van de grafiek interpoleren, ongeacht het bereik van de grafiek. Soortgelijke gegevens die op een lineaire schaal worden uitgezet, zijn minder duidelijk.
Oplossen van problemen met logaritmische grafieken
Een belangrijk punt bij het gebruik van logaritmische grafieken om problemen op te lossen, is dat ze de schaal zodanig vergroten dat grote gegevensbereiken zinvoller worden. In de vergelijking hierboven (j^*= \sigma T^4), zou het uitzetten van j tegen T de verwachte kromme opleveren, maar de schaal zou zodanig zijn dat minieme veranderingen onopgemerkt blijven en de grootschalige effecten van de relatie de grafiek overheersen: Het is zo groot dat de “interessante gebieden” niet op een leesbare schaal op het papier passen.
Het nemen van de logaritme van elke zijde van de vergelijkingen levert op: logj=log{(\tau ) }^4 . We baseren ons nu op de eigenschappen van logaritmen om de vergelijking te herschrijven.
Herinner je de volgende eigenschappen van logaritmen:
log(ab)=log(a)+log(b) ^b=(b)log(a)
Met behulp van het bovenstaande wordt onze vergelijking:
begin{align} &=4 log{(\sigma\tau ) } &=4log{(\sigma)}+4log{(\tau ) } &=4\log{(\tau ) }+4\log{(\sigma)} \einde{align}