De Heaviside-stappenfunctie is een wiskundige functie die 
wordt genoemd, of soms 
of 
(Abramowitz and Stegun 1972, p. 1020), en ook bekend als de “eenheidsstapfunctie”. De term “Heaviside stapfunctie” en het symbool ervan kunnen zowel een stukgewijze constante functie als een veralgemeende functie voorstellen.
Wanneer de Heaviside-stapfunctie is gedefinieerd als een stukgewijze constante functie, wordt zij gegeven door
 |
(1)
|
(Abramowitz and Stegun 1972, p. 1020; Bracewell 2000, p. 61). De grafiek hierboven toont deze functie (linker figuur), en hoe hij eruit zou zien als hij op een oscilloscoop zou worden weergegeven (rechter figuur).
Wanneer gedefinieerd als een gegeneraliseerde functie, kan deze worden gedefinieerd als een functie 
zo dat
 |
(2)
|
voor 
de afgeleide van een voldoende gladde functie 
die voldoende snel vervalt (Kanwal 1998).
De Wolfram-taal stelt de gegeneraliseerde functie van Heaviside voor als HeavisideTheta, terwijl UnitStep wordt gebruikt om de functie Piecewise voor te stellen (die, zo moet worden opgemerkt, de conventie 
aanneemt in plaats van de conventionele definitie 
).
De stenografische notatie
 |
(3)
|
wordt soms ook gebruikt.
De Heaviside-stappenfunctie is gerelateerd aan de boxcarfunctie door
 |
(4)
|
en kan worden gedefinieerd in termen van de tekenfunctie door
 |
(5)
|
De afgeleide van de stapfunctie wordt gegeven door
 |
(6)
|
waarbij 
de deltafunctie is (Bracewell 2000, p. 97).
De Heaviside-stappenfunctie is gerelateerd aan de hellingbaanfunctie 
door
 |
(7)
|
en aan de afgeleide van 
door
 |
(8)
|
De twee zijn ook verbonden door
 |
(9)
|
waarbij 
convolutie aanduidt.
Bracewell (2000) geeft vele identiteiten, waaronder de volgende. Wanneer 
de convolutie aanduidt,
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
Daarnaast,
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
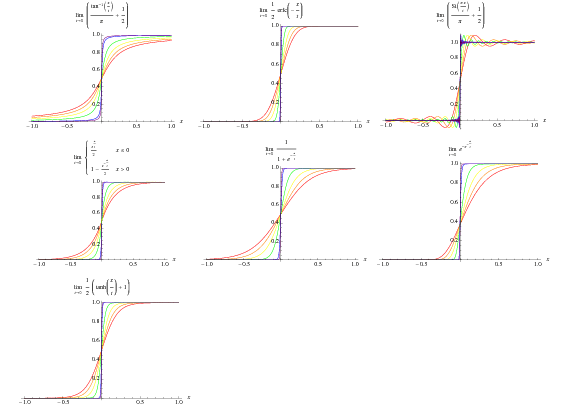
De Heaviside-stapfunctie kan worden gedefinieerd door de volgende limieten,
 |
 |
 |
(17)
|
|
 |
 |
 |
|
(18)
|
 |
 |
 |
(19)
|
|
 |
 |
 |
(20)
|
|
 |
 |
 |
(21)
|
|
 |
 |
 |
(22)
|
|
 |
 |
 |
(23)
|
|
 |
 |
 |
(24)
|
|
 |
 |
 |
(25)
|
|
 |
 |
 |
(26)
|
|
 |
 |
 |
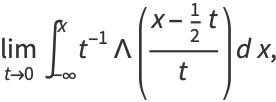(27)
|
waarbij 
de erfc-functie is, 
de sinus-integraal is, 
de sinc-functie is, en 
de driehoeksfunctie met één argument is. De eerste vier zijn hierboven geïllustreerd voor 
, 0.1, en 0.01.
Natuurlijk is elke monotone functie met constante ongelijke horizontale asymptoten een Heaviside stapfunctie onder gepaste schaalvergroting en eventuele spiegeling. De Fourier-transformatie van de Heaviside-stappenfunctie wordt gegeven door
 |
 |
 |
(28)
|
 |
 |
 |
(29)
|
waarbij 
de deltafunctie is.