Een 
matrix 
is een orthogonale matrix als
 |
(1)
|
waar 
de getransponeerde is van 
en 
de identiteitsmatrix is. In het bijzonder is een orthogonale matrix altijd inverteerbaar, en
 |
(2)
|
In componentvorm,
 |
(3)
|
Dit verband maakt orthogonale matrices bijzonder gemakkelijk om mee te rekenen, aangezien de transpositiebewerking veel eenvoudiger is dan het berekenen van een inverse.
Bijvoorbeeld,
 |
 |
 |
(4)
|
 |
 |
 |
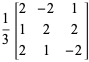(5)
|
zijn orthogonale matrices.
Een matrix 
kan in de Wolfram Language worden getest om te zien of hij orthogonaal is met OrthogonalMatrixQ.
De rijen van een orthogonale matrix vormen een orthonormale basis. Dat wil zeggen, elke rij heeft lengte één, en staan onderling loodrecht op elkaar. Ook de kolommen vormen een orthonormale basis. In feite, gegeven elke orthonormale basis, is de matrix waarvan de rijen die basis vormen een orthogonale matrix. Het is automatisch zo dat de kolommen ook een orthonormale basis zijn.
De orthogonale matrices zijn precies die matrices die het binnenproduct behouden
 |
(6)
|
Ook, de determinant van 
is ofwel 1 ofwel 
. Als deelverzameling van 
zijn de orthogonale matrices niet verbonden omdat de determinant een continue functie is. In plaats daarvan zijn er twee componenten die overeenkomen met of de determinant 1 of 
is. De orthogonale matrices met 
zijn rotaties, en zo’n matrix wordt een speciale orthogonale matrix genoemd.
Het matrixproduct van twee orthogonale matrices is weer een orthogonale matrix. Bovendien is de inverse van een orthogonale matrix een orthogonale matrix, evenals de identiteitsmatrix. Vandaar dat de verzameling van orthogonale matrices een groep vormen, genaamd de orthogonale groep 
.