![]()
Een vectorbasis van een vectorruimte ![]() is gedefinieerd als een deelverzameling
is gedefinieerd als een deelverzameling ![]() van vectoren in
van vectoren in ![]() die lineair onafhankelijk zijn en
die lineair onafhankelijk zijn en ![]() overspannen. Bijgevolg, als
overspannen. Bijgevolg, als ![]() een lijst vectoren is in
een lijst vectoren is in ![]() , dan vormen deze vectoren een vectorbasis als en slechts als elke
, dan vormen deze vectoren een vectorbasis als en slechts als elke ![]() uniek geschreven kan worden als
uniek geschreven kan worden als
|
(1)
|
waar ![]()
![]() elementen van het basisveld zijn.
elementen van het basisveld zijn.
Wanneer het basisveld de reals is zodat ![]() voor
voor ![]() , zijn de resulterende basisvectoren
, zijn de resulterende basisvectoren ![]() -tupels van reals die
-tupels van reals die ![]() -dimensionale Euclidische ruimte
-dimensionale Euclidische ruimte ![]() overspannen. Andere mogelijke basisvelden zijn de complexen
overspannen. Andere mogelijke basisvelden zijn de complexen ![]() , en verschillende positieve karakteristieke velden die in de algebra, getaltheorie en algebraïsche meetkunde voorkomen.
, en verschillende positieve karakteristieke velden die in de algebra, getaltheorie en algebraïsche meetkunde voorkomen.
Een vectorruimte ![]() heeft veel verschillende vectorbasissen, maar er zijn altijd evenveel basisvectoren in elk van hen. Het aantal basisvectoren in
heeft veel verschillende vectorbasissen, maar er zijn altijd evenveel basisvectoren in elk van hen. Het aantal basisvectoren in ![]() wordt de dimensie van
wordt de dimensie van ![]() genoemd. Elke overspannen lijst in een vectorruimte kan worden herleid tot een basis van de vectorruimte.
genoemd. Elke overspannen lijst in een vectorruimte kan worden herleid tot een basis van de vectorruimte.
Het eenvoudigste voorbeeld van een vectorbasis is de standaardbasis in de euclidische ruimte ![]() , waarin de basisvectoren langs elke coördinatenas liggen. Een verandering van basis kan worden gebruikt om vectoren (en operatoren) in een gegeven basis om te zetten in een andere.
, waarin de basisvectoren langs elke coördinatenas liggen. Een verandering van basis kan worden gebruikt om vectoren (en operatoren) in een gegeven basis om te zetten in een andere.
Gegeven een hypervlak gedefinieerd door
|
(2)
|
een basis kan worden gevonden door ![]() op te lossen in termen van
op te lossen in termen van ![]()
![]()
![]() , en
, en ![]() . Als we deze procedure uitvoeren,
. Als we deze procedure uitvoeren,
|
(3)
|
so
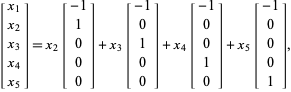 |
(4)
|
en de bovenstaande vectoren vormen een (niet genormaliseerde) basis.
Gegeven een matrix ![]() met een orthonormale basis, is de matrix die overeenkomt met een verandering van basis, uitgedrukt in termen van de oorspronkelijke
met een orthonormale basis, is de matrix die overeenkomt met een verandering van basis, uitgedrukt in termen van de oorspronkelijke ![]() is
is
|
(5)
|
Wanneer een vectorruimte oneindig dimensionaal is, dan bestaat er een basis zolang men uitgaat van het axioma van keuze. Een deelverzameling van de basis die lineair onafhankelijk is en waarvan de spanwijdte dicht is, heet een volledige verzameling, en is vergelijkbaar met een basis. Als ![]() een Hilbertruimte is, dan heet een volledige verzameling een Hilbertbasis.
een Hilbertruimte is, dan heet een volledige verzameling een Hilbertbasis.