Objectivos de Aprendizagem
No final desta secção, será capaz de o fazer:
- Explicar um cenário em que os campos magnéticos e eléctricos são cruzados e as suas forças se equilibram à medida que uma partícula carregada se move através de um selector de velocidade
- Comparar como os portadores de carga se movem num material condutor e explicar como isto se relaciona com o efeito Hall
Em 1879, E.H. Hall concebeu uma experiência que pode ser utilizada para identificar o sinal dos portadores de carga predominantes num material condutor. De uma perspectiva histórica, esta experiência foi a primeira a demonstrar que os portadores de carga na maioria dos metais são negativos.
p>Visitar este website para encontrar mais informações sobre o efeito Hall.
Nós investigamos o efeito Hall através do estudo do movimento dos electrões livres ao longo de uma faixa metálica de largura l num campo magnético constante (Figura \PageIndex{1}}). Os electrões movem-se da esquerda para a direita, pelo que a força magnética que experimentam os empurra para a extremidade inferior da faixa. Isto deixa um excesso de carga positiva na borda superior da tira, resultando num campo eléctrico E dirigido de cima para baixo. A concentração de carga em ambos os bordos acumula-se até que a força eléctrica sobre os electrões numa direcção seja equilibrada pela força magnética sobre eles na direcção oposta. O equilíbrio é alcançado quando:
\\
p> onde e é a magnitude da carga de electrões, \(v_d\) é a velocidade de deriva dos electrões, e E é a magnitude do campo eléctrico criado pela carga separada. Resolvendo isto para a velocidade de deriva resulta em
/p>
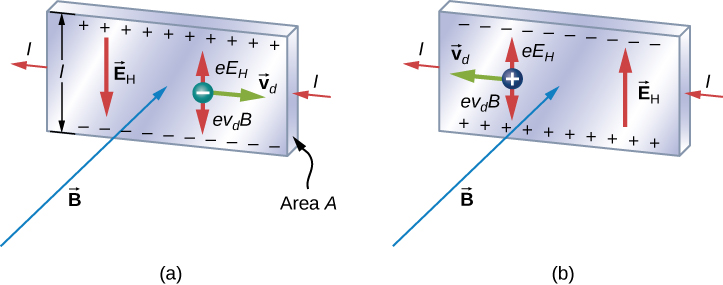
Um cenário onde os campos eléctricos e magnéticos são perpendiculares um ao outro é chamado de situação de campo cruzado. Se estes campos produzem forças iguais e opostas sobre uma partícula carregada com a velocidade que iguala as forças, estas partículas são capazes de passar através de um aparelho, chamado selector de velocidade, sem serem desviadas. Esta velocidade é representada na equação \ref{11.26}. Qualquer outra velocidade de uma partícula carregada enviada para os mesmos campos seria desviada pela força magnética ou força eléctrica.
Voltando ao efeito Hall, se a corrente na faixa for I, então de Corrente e Resistência, sabemos que
>p>> onde n é o número de portadores de carga por volume e A é a área da secção transversal da faixa. Combinando as equações para \(v_d\) e I resulta em
O campo E está relacionado com a diferença potencial V entre as bordas da tira por
>p>>>p> A quantidade \(V\) é chamada potencial Hall e pode ser medida com um voltímetro. Finalmente, a combinação das equações de I e E dá-nos
onde a borda superior da tira na Figura \\(\PageIndex{1}} é positiva em relação à borda inferior.
Também podemos combinar a Equação \ref{11.24} e Equação {11.28} para obter uma expressão para a tensão de Hall em termos do campo magnético:
>p>
E se os portadores de carga forem positivos, como na Figura {1}(PageIndex{1})? Para a mesma corrente I, a magnitude de V ainda é dada pela Equação {hallV}. No entanto, o bordo superior é agora negativo em relação ao bordo inferior. Portanto, medindo simplesmente o sinal de V, podemos determinar o sinal dos portadores de carga maioritários num metal.
Medições com potencial de queda mostram que os electrões são os portadores de carga dominantes na maioria dos metais. Contudo, os potenciais Hall indicam que para alguns metais, tais como tungsténio, berílio, e muitos semicondutores, a maioria dos portadores de carga são positivos. Acontece que a condução por carga positiva é causada pela migração de sítios de electrões em falta (chamados buracos) sobre iões. A condução por furos é estudada mais tarde em Física da Matéria Condensada.
O efeito Hall pode ser usado para medir campos magnéticos. Se um material com uma densidade conhecida de portadores de carga n for colocado num campo magnético e V for medido, então o campo pode ser determinado a partir da Equação \ref{11.29}. Em laboratórios de investigação onde os campos de electroímanes utilizados para medições precisas têm de ser extremamente estáveis, uma “sonda Hall” é normalmente utilizada como parte de um circuito electrónico que regula o campo.
Exemplo \\(\PageIndex{1}}): Selector de Velocidade
Um feixe de electrões entra num selector de velocidade de campo cruzado com campos magnéticos e eléctricos de 2,0 mT e \(6,0 ^3 ^3, N/C), respectivamente. (a) Qual deve ser a velocidade do feixe de electrões para atravessar os campos cruzados sem ser desviado? Se o campo eléctrico for desligado, (b) qual é a aceleração do feixe de electrões e (c) qual é o raio do movimento circular que resulta?
Estratégia
O feixe de electrões não é desviado por nenhum dos campos magnéticos ou eléctricos se estas forças forem equilibradas. Com base nestas forças equilibradas, calculamos a velocidade do feixe. Sem o campo eléctrico, apenas a força magnética é utilizada na segunda lei de Newton para encontrar a aceleração. Finalmente, o raio do caminho é baseado no movimento circular resultante da força magnética.
Solução
- A velocidade do feixe não perturbado de electrões com campos cruzados é calculada pela Equação \ref{11,25}: \
- A aceleração é calculada a partir da força líquida do campo magnético, igual à massa vezes a aceleração. A magnitude da aceleração é: \ O raio do caminho vem de um equilíbrio das forças circulares e magnéticas, ou Equação {11.25}: {11.25}: \
Significado
Se os electrões no feixe tivessem velocidades acima ou abaixo da resposta em parte (a), esses electrões teriam uma força líquida mais forte exercida quer pelo campo magnético quer pelo campo eléctrico. Portanto, apenas aqueles electrões a esta velocidade específica conseguiriam passar.
O Potencial Hall numa Fita de Prata
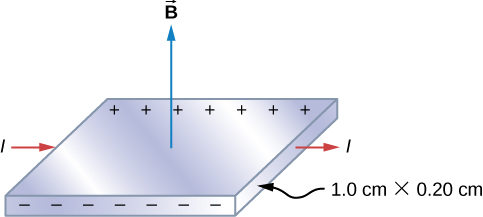
Figure \(\PageIndex{2}}} mostra uma fita de prata cuja secção transversal é de 1,0 cm por 0,20 cm. A fita carrega uma corrente de 100 A da esquerda para a direita, e encontra-se num campo magnético uniforme de magnitude 1,5 T. Usando um valor de densidade de ^(n = 5,9 ^{28}} electrões por metro cúbico para a prata, encontrar o potencial Hall entre as bordas da fita.
Estratégia
p>Desde que a maioria dos portadores de carga são electrões, a polaridade da voltagem de Hall é a indicada na figura. O valor da voltagem de Hall é calculado usando a equação \ref{hallV}.
Solução
Ao calcular a voltagem de Hall, precisamos de conhecer a corrente através do material, o campo magnético, o comprimento, o número de portadores de carga, e a área. Uma vez que todas estas são dadas, a voltagem de Hall é calculada como:
\ &= \frac{(100 \, A)(1.5 \, T)(1.0 ^{-2}m)}{(5.9 ^{28} /m^3)(1.6 ^{-19}C)(2.0 ^^^ vezes 10^{-5}m^2)}{(5.9 ^^ vezes 10^{28} /m^3)(1.6 ^^ vezes 10^{-19}C)(2.0 ^ vezes 10^{-5}m^2)} &= 7,9 vezes 10^{-6}V. \end{align*} \]
Significado
Como neste exemplo, o potencial do Salão é geralmente muito pequeno, e é necessária uma experimentação cuidadosa com equipamento sensível para a sua medição.
Exercicio \\(\PageIndex{1})
p> Uma sonda Hall consiste numa tira de cobre, \(n = 8,5 \\\\\\\\\\P(n = 8,5 \P(28)) electrões por metro cúbico, que tem 2,0 cm de largura e 0,10 cm de espessura. Qual é o campo magnético quando I = 50 A e o potencial Hall é
- \(4.0 \, \u V\) e
- (6.0 \, \u V\)?
/ol> Responda a
1.1 T
Responda b
1.6 T
Contribuintes e Atribuições
- p>Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs com muitos autores contribuintes. Esta obra é licenciada pela OpenStax University Physics sob uma licença Creative Commons Attribution License (por 4.0).