br>![]()
Uma base vectorial de um espaço vectorial ![]() é definida como um subconjunto
é definida como um subconjunto ![]() de vectores em
de vectores em ![]() que são linearmente independentes e vão
que são linearmente independentes e vão ![]() . Consequentemente, se
. Consequentemente, se ![]() é uma lista de vectores em
é uma lista de vectores em ![]() , então estes vectores formam uma base vectorial se e só se cada
, então estes vectores formam uma base vectorial se e só se cada ![]() puder ser unicamente escrito como
puder ser unicamente escrito como
|
(1)
|
where ![]()
![]() são elementos do campo base.
são elementos do campo base.
Quando o campo base é os reais de modo que ![]() para
para ![]() , os vectores de base resultantes são
, os vectores de base resultantes são ![]() -tuplos de reais que abrangem
-tuplos de reais que abrangem ![]() -espaço euclidiano dimensional
-espaço euclidiano dimensional ![]() . Outros campos base possíveis incluem os complexos
. Outros campos base possíveis incluem os complexos ![]() , bem como vários campos de característica positiva considerados em álgebra, teoria dos números, e geometria algébrica.
, bem como vários campos de característica positiva considerados em álgebra, teoria dos números, e geometria algébrica.
um espaço vectorial ![]() tem muitas bases vectoriais diferentes, mas há sempre o mesmo número de vectores base em cada um deles. O número de vectores de base em
tem muitas bases vectoriais diferentes, mas há sempre o mesmo número de vectores base em cada um deles. O número de vectores de base em ![]() chama-se a dimensão de
chama-se a dimensão de ![]() . Cada lista de vectores num espaço vectorial pode ser reduzida a uma base do espaço vectorial.
. Cada lista de vectores num espaço vectorial pode ser reduzida a uma base do espaço vectorial.
O exemplo mais simples de uma base vectorial é a base padrão no espaço euclidiano ![]() , na qual os vectores base se encontram ao longo de cada eixo de coordenadas. Uma mudança de base pode ser utilizada para transformar vectores (e operadores) numa dada base para outra.
, na qual os vectores base se encontram ao longo de cada eixo de coordenadas. Uma mudança de base pode ser utilizada para transformar vectores (e operadores) numa dada base para outra.
Dado um hiperplano definido por
|
(2)
|
a pode ser encontrada resolvendo para ![]() em termos de
em termos de ![]()
![]()
![]() , e
, e ![]() . Executando este procedimento,
. Executando este procedimento,
|
(3)
|
so
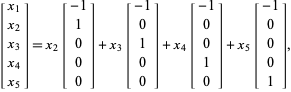 |
(4)
|
e os vectores acima referidos formam uma base (não normalizada).
![]() A com uma base orto-normal, a matriz correspondente a uma mudança de base, expressa em termos do original
A com uma base orto-normal, a matriz correspondente a uma mudança de base, expressa em termos do original ![]() is
is
|
(5)
|
Quando um espaço vectorial é de dimensão infinita, então existe uma base desde que se assuma o axioma de escolha. Um subconjunto da base que é linearmente independente e cujo vão é denso é chamado um conjunto completo, e é semelhante a uma base. Quando ![]() é um espaço Hilbert, um conjunto completo é chamado de base Hilbert.
é um espaço Hilbert, um conjunto completo é chamado de base Hilbert.