Na nossa lição anterior, estudámos como usar a Regra de Cramer com duas variáveis. O nosso objectivo aqui é expandir a aplicação da Regra de Cramer para três variáveis geralmente em termos de {x}, {y}, e {z}. Passo a cinco (5) exemplos trabalhados para o ajudar a familiarizar-se com este conceito.
Para se sair bem neste tópico, é preciso ter uma ideia de como encontrar o determinante de uma matriz 3⨉3. Portanto, isto é o que vamos fazer primeiro. Pronto?
Formula para encontrar o determinante de uma Matriz 3⨉3
- Deu uma matriz 3⨉3

- Its determinant pode ser calculado usando a seguinte fórmula.
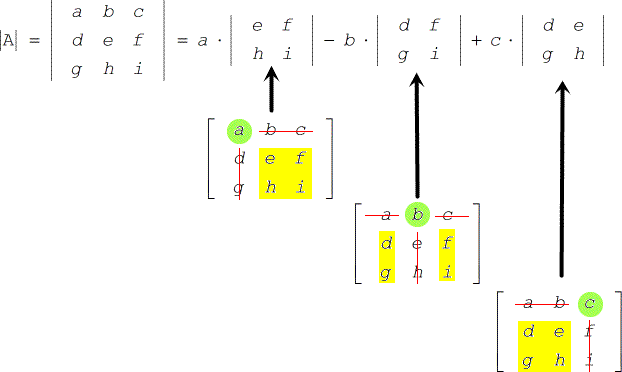
Vamos fazer um exemplo rápido disto.
P>P>Ponham o determinante da matriz A
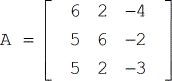
Solução: Certifique-se de que segue cuidadosamente a fórmula sobre como encontrar o determinante de uma matriz 3×3, como mostrado acima. Mais ainda, não se apresse quando efectuar as operações aritméticas necessárias em cada passo. É aqui que normalmente ocorrem erros comuns, mas estes podem ser evitados. Quando o fizer correctamente, a sua solução deve ser semelhante à abaixo.
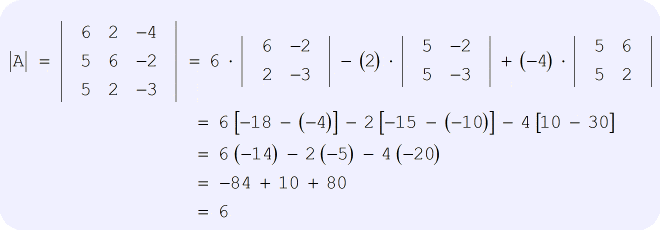
Agora, é altura de rever o procedimento sobre como usar a Regra de Cramer num sistema linear envolvendo três variáveis.
Regra de Cramer para Sistemas de Equações Lineares com Três Variáveis
- li>Div um sistema linear

- li>Etiquetagem de cada uma das quatro matrizes
matriz eficiente:
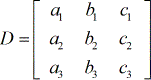
X – matriz:
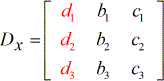
Y – matriz:
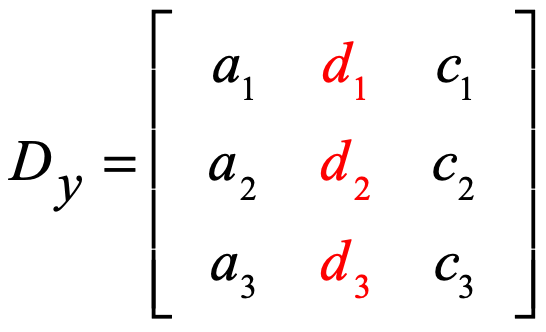
Z – matriz:
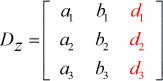
- para resolver para x:
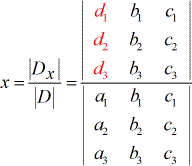
- para resolver por y:
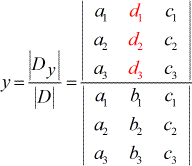
- para resolver para z:
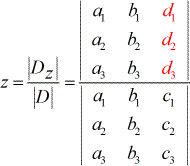
Coisas a observar a partir da configuração acima:
1) Os coeficientes das variáveis x, y, e z fazem uso das subscritas a, b, e c, respectivamente. Enquanto os termos constantes utilizam os subscritos d.
2) Os denominadores para encontrar os valores de x, y, e z são todos os mesmos, o que é o determinante da matriz de coeficientes (coeficientes provenientes das colunas de x, y, e z).
3) Para resolver para x, os coeficientes da coluna de x são substituídos pela coluna constante (a vermelho).
4) Para resolver para y, os coeficientes da coluna de y são substituídos pela coluna constante (a vermelho).
5) Da mesma forma, para resolver para z, os coeficientes da coluna z são substituídos pela coluna constante (a vermelho).
Exemplos de Como Resolver Sistemas de Equações Lineares com Três Variáveis usando a Regra de Cramer
Exemplo 1: Resolver o sistema com três variáveis pela Regra de Cramer.
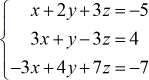
Do sistema dado de equações lineares, Vou construir as quatro matrizes que serão usadas para resolver para os valores de {\i1}large{\i}color{\i}x, {\i}large{\i}color{\i}y, e {\i}large{\i}z{\i}color
Utiliza o guia acima para configurar correctamente estas matrizes especiais.
- matriz eficiente
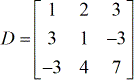
- X – matriz
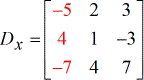
- Y – matriz
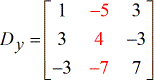
- Z – matriz
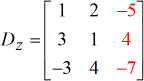
Next, eu resolverei para o determinante de cada matriz. Para o fazer, posso resolver manualmente o determinante de cada matriz em papel, utilizando a fórmula fornecida acima. Pode ser aborrecido, mas não faz mal, uma vez que as boas capacidades matemáticas são desenvolvidas através de muitos problemas.
Os valores dos determinantes são listados abaixo.
determinantes de cada matriz:
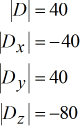
As respostas ou soluções finais são facilmente computadas ou calculadas uma vez encontrados todos os determinantes necessários.
Valores resolvidos para {\i1}grande{\i}x, {\i}grande{\i}y}, e {\i}grande{\i}z}.
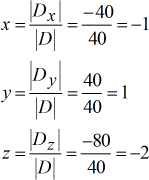
A resposta final escrita na notação de ponto é \ cor (azul) esquerda( {x,y,z} {x,direita) = \ esquerda( { – 1,1, – 2} \ direita).
Exemplo 2: Resolver o sistema com três variáveis pela Regra de Cramer.
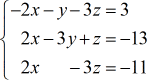
Considero a matriz do coeficiente como a matriz “primária” porque as outras três matrizes são derivadas dela. Por exemplo, a matriz x é apenas a matriz “primária” com a coluna x substituída pela coluna constante (em vermelho). Pode-se observar que o mesmo padrão é aplicado na construção das outras matrizes: y e z.
- matriz coeficiente
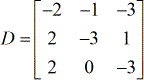
- X – matriz
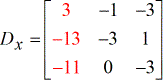
- Y – matriz
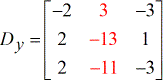
- Z – matriz
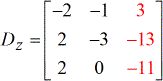
Depois de resolver o determinante de cada matriz, tenho-os todos escritos.
determinantes de cada matriz:
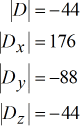
Os valores para x, y e z são calculados como se segue. Note-se que x é obtido tomando o determinante da matriz x dividido pelo determinante da matriz do coeficiente. Esta regra aplica-se ao resto.
Valores resolvidos para \large{\color{\verde}x}, \large{\verde{\verde}y}, e \large{\verde{\verde}z}.
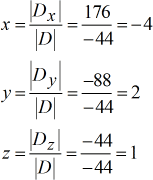
A nossa resposta final é \ cor{blue}{esquerda( {x,y,z} {direita) = \querda( { – \,4,2,1} \direita).
Exemplo 3: Resolver o sistema com três variáveis pela Regra de Cramer.
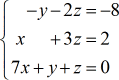
Este problema é muito mais fácil do que os dois primeiros exemplos devido à presença de entradas zero nas colunas x, y, e constantes. Está a vê-lo? Quando temos zero entradas numa matriz, o cálculo da sua determinação é dramaticamente simplificado.
De facto, à medida que se aumenta o número de zeros numa matriz quadrada, o trabalho feito para encontrar o seu determinante é grandemente reduzido.
Aqui estão as matrizes extraídas do sistema de equações lineares.
- matriz eficiente
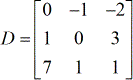
- X – matriz
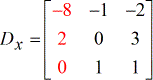
- Y – matriz
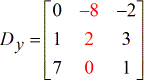
- Z – matriz
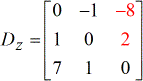
Solvendo os seus determinantes, obtive os seguintes valores.
determinantes de cada matriz:
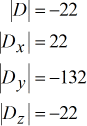
Isto leva-nos a configurar e calcular facilmente as respostas finais.
Valores resolvidos para |larga (verde)x, |larga (verde)y}, e |larga (verde)z}.
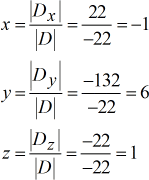
A resposta final é \ cor{blue}{esquerda( {x,y,z} {direita) = \ esquerda( { – \,1,6,1} {direita).
Exemplo 4: Resolver o sistema com três variáveis pela Regra de Cramer
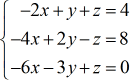
Escreva as quatro matrizes especiais.
- matriz eficiente
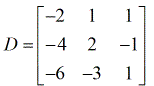
- X – matriz
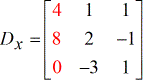
- Y – matriz
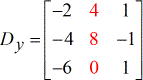
- Z – matriz
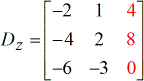
Evalue cada matriz para encontrar o seu determinante.
Estes são os determinantes de cada matriz:
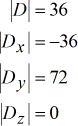
Utilizar a Regra de Cramer para obter as seguintes soluções.
Valores resolvidos para {\i1}large{\i}color{\i}x}, {\i}large{\i}color{\i}y}, e {\i}large{\i}color{\i}z}.
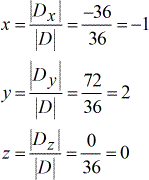
A resposta final é \ cor{blue}{esquerda( {x,y,z} {direita) = \ esquerda( { – \,1,2,0} {direita).
Exemplo 5: Resolver o sistema com três variáveis pela Regra de Cramer
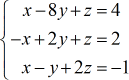
Vamos fazer um exemplo final! Espero que neste momento já tenha tido prática suficiente sobre como resolver sistemas com três variáveis usando a Regra de Cramer.
Sugiro que primeiro resolva isto no papel e depois volte para comparar a sua resposta. Não se preocupe, ninguém está a ver. 👀 Quando estiver pronto, desça para ver a solução.

Construa as quatro matrizes especiais.
- matriz eficiente
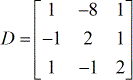
- X – matriz
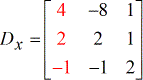
- Y – matriz
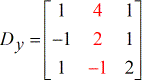
- Z – matriz
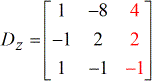
P>P>Encontrar o determinante de cada matriz quadrada.
Determinantes de cada matriz
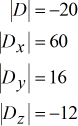
Solve para x, y e z usando a fórmula dada.
p>Valores resolvidos para \larga{\i}, \i}, e \i}larga{\i}color{\i}y, e \i}larga{\i}color{\i}z
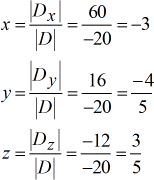
Done! A resposta final em forma de ponto é: {{x,y,z}{esquerda( {x,y,z}direita) = {esquerda( { -,3, – 4 acima de 5},{3 acima de 5}},{3 acima de 5}}{direita).
Prática com folhas de trabalho
P>Pode também estar interessado em:
Regra do Cramer 2×2