Objectivos de aprendizagem
No final desta secção, poderá:
- Explicar linhas equipotenciais e superfícies equipotenciais.
- Descrever a acção da ligação à terra de um aparelho eléctrico.
- Comparar campo eléctrico e linhas equipotenciais.
Podemos representar os potenciais eléctricos (voltagens) pictóricos, tal como desenhámos imagens para ilustrar campos eléctricos. Naturalmente, os dois estão relacionados. Considere-se a Figura 1, que mostra uma carga de ponto positivo isolado e as suas linhas de campo eléctrico. As linhas de campo eléctrico irradiam de uma carga positiva e terminam em cargas negativas. Enquanto utilizamos setas azuis para representar a magnitude e direcção do campo eléctrico, utilizamos linhas verdes para representar locais onde o potencial eléctrico é constante. Estas são chamadas linhas equipotenciais em duas dimensões, ou superfícies equipotenciais em três dimensões. O termo equipotencial é também utilizado como substantivo, referindo-se a uma linha ou superfície equipotencial. O potencial para uma carga pontual é o mesmo em qualquer lugar numa esfera imaginária de raio r que rodeia a carga. Isto é verdade uma vez que o potencial para uma carga pontual é dado por V=\frac{kQ}{r} e, portanto, tem o mesmo valor em qualquer ponto que esteja a uma dada distância r da carga. Uma esfera equipotencial é um círculo na visão bidimensional da Figura 1. Uma vez que as linhas do campo eléctrico apontam radialmente para longe da carga, são perpendiculares às linhas equipotenciais.

Figure 1. Uma carga de ponto isolado Q com as suas linhas de campo eléctrico em azul e linhas equipotenciais em verde. O potencial é o mesmo ao longo de cada linha equipotencial, o que significa que não é necessário nenhum trabalho para mover uma carga para qualquer lugar ao longo de uma dessas linhas. É necessário trabalho para deslocar uma carga de uma linha equipotencial para outra. As linhas equipotenciais são sempre perpendiculares às linhas do campo eléctrico.
É importante notar que as linhas equipotenciais são sempre perpendiculares às linhas do campo eléctrico. Não é necessário trabalho para mover uma carga ao longo de um equipotencial, uma vez que ΔV = 0. Assim o trabalho é
W = -ΔPE = -qΔV = 0.
Work é zero se a força for perpendicular ao movimento. A força está na mesma direcção que E, de modo que o movimento ao longo de um equipotencial deve ser perpendicular a E. Mais precisamente, o trabalho está relacionado com o campo eléctrico por
W = Fd cos θ = qEd cos θ = 0.
Nota que na equação acima, E e F simbolizam as magnitudes da força e da força do campo eléctrico, respectivamente. Nem q nem E nem d é zero, e assim porque θ deve ser 0, o que significa que θ deve ser 90º. Por outras palavras, o movimento ao longo de um equipotencial é perpendicular a E.
Uma das regras para campos eléctricos estáticos e condutores é que o campo eléctrico deve ser perpendicular à superfície de qualquer condutor. Isto implica que um condutor é uma superfície equipotencial em situações estáticas. Não pode haver diferença de voltagem através da superfície de um condutor, ou as cargas irão fluir. Uma das utilizações deste facto é que um condutor pode ser fixado a zero volts, ligando-o à terra com um bom condutor – um processo chamado aterramento. A ligação à terra pode ser uma ferramenta de segurança útil. Por exemplo, a ligação à terra da caixa metálica de um aparelho eléctrico assegura que está a zero volts em relação à terra.
Terra
Um condutor pode ser fixado a zero volts ligando-o à terra com um bom condutor – um processo chamado aterramento.
Porque um condutor é um equipotencial, pode substituir qualquer superfície equipotencial. Por exemplo, na Figura 1, um condutor esférico carregado pode substituir a carga pontual, e o campo eléctrico e as superfícies potenciais fora dele permanecerão inalterados, confirmando a alegação de que uma distribuição de carga esférica é equivalente a uma carga pontual no seu centro.
Figure 2 mostra o campo eléctrico e as linhas equipotenciais para duas cargas iguais e opostas. Dadas as linhas do campo eléctrico, as linhas equipotenciais podem ser desenhadas simplesmente tornando-as perpendiculares às linhas do campo eléctrico. Pelo contrário, dadas as linhas equipotenciais, como na Figura 3a, as linhas do campo eléctrico podem ser desenhadas tornando-as perpendiculares aos equipotenciais, como na Figura 3b.

Figure 2. As linhas de campo eléctrico e linhas equipotenciais para duas cargas iguais mas opostas. As linhas equipotenciais podem ser desenhadas tornando-as perpendiculares às linhas do campo eléctrico, se estas forem conhecidas. Note-se que o potencial é maior (mais positivo) perto da carga positiva e menor (mais negativo) perto da carga negativa.

Figure 3. (a) Estas linhas equipotenciais podem ser medidas com um voltímetro, numa experiência de laboratório. (b) As linhas de campo eléctrico correspondentes são encontradas desenhando-as perpendicularmente aos equipotenciais. Note-se que estes campos são consistentes com duas cargas negativas iguais.

Figure 4. O campo eléctrico e as linhas equipotenciais entre duas placas metálicas.
Um dos casos mais importantes é o das placas condutoras paralelas familiares mostradas na Figura 4. Entre as placas, os equipotenciais estão uniformemente espaçados e paralelos. O mesmo campo poderia ser mantido colocando placas condutoras nas linhas equipotenciais nos potenciais mostrados.
Uma aplicação importante de campos eléctricos e linhas equipotenciais envolve o coração. O coração depende de sinais eléctricos para manter o seu ritmo. O movimento dos sinais eléctricos faz com que as câmaras do coração se contraiam e relaxem. Quando uma pessoa tem um ataque cardíaco, o movimento destes sinais eléctricos pode ser perturbado. Um pacemaker artificial e um desfibrilador podem ser utilizados para iniciar o ritmo dos sinais eléctricos. As linhas equipotenciais em torno do coração, a região torácica e o eixo do coração são formas úteis de monitorizar a estrutura e as funções do coração. Um electrocardiograma (ECG) mede os pequenos sinais eléctricos que estão a ser gerados durante a actividade do coração. Mais sobre a relação entre os campos eléctricos e o coração é discutida em Energy Stored in Capacitors.
PhET Explorations: Cargas e Campos
Mover cargas pontuais no campo de jogo e depois ver o campo eléctrico, tensões, linhas equipotenciais, e muito mais. É colorido, é dinâmico, é livre.
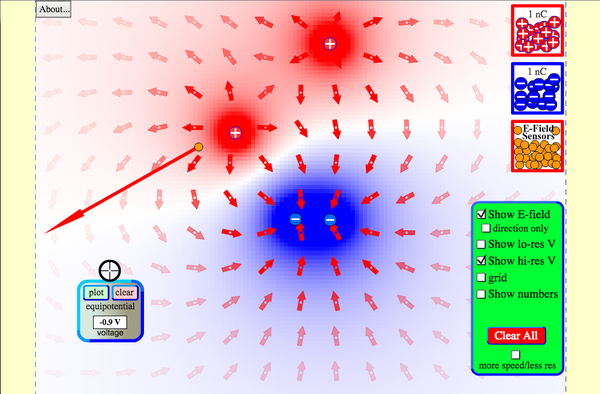
Clique para executar a simulação.
Secção Sumário
- Uma linha equipotencial é uma linha ao longo da qual o potencial eléctrico é constante.
- Uma superfície equipotencial é uma versão tridimensional de linhas equipotenciais.
- As linhas equipotenciais são sempre perpendiculares às linhas do campo eléctrico.
- O processo pelo qual um condutor pode ser fixado a zero volts ligando-o à terra com um bom condutor chama-se aterramento.
Perguntas conceptuais
- O que é uma linha equipotencial? O que é uma superfície equipotencial?
- Explique nas suas próprias palavras porque é que as linhas e superfícies equipotenciais devem ser perpendiculares às linhas do campo eléctrico.
- Pode as diferentes linhas equipotenciais cruzarem-se? Explique.
Problemas & Exercícios
- (a) Esboce as linhas equipotenciais perto de uma carga pontual +q. Indicar a direcção do potencial de aumento. (b) Fazer o mesmo para uma carga pontual -3q.
- Desenhar as linhas equipotenciais para as duas cargas positivas iguais mostradas na Figura 5. Indicar a direcção do potencial crescente.

Figure 5. O campo eléctrico próximo de duas cargas positivas iguais é dirigido para longe de cada uma das cargas.
- Figure 6 mostra as linhas do campo eléctrico próximas de duas cargas q1 e q2, tendo a primeira uma magnitude quatro vezes superior à da segunda. Traçar as linhas equipotenciais para estas duas cargas, e indicar a direcção do potencial crescente.
- Traçar as linhas equipotenciais a uma longa distância das cargas mostradas na Figura 6. Indicar a direcção do potencial crescente.

Figure 6. O campo eléctrico próximo de duas cargas.
- Desenhar as linhas equipotenciais na proximidade de duas cargas opostas, onde a carga negativa é três vezes maior em magnitude do que a positiva. Ver Figura 6 para uma situação semelhante. Indicar a direcção do potencial crescente.
- Desenhar as linhas equipotenciais na proximidade do condutor carregado negativamente na Figura 7. Como irão estes equipotenciais parecer a uma longa distância do objecto?

Figure 7. Um condutor carregado negativamente.
- Descreve as linhas equipotenciais que rodeiam as duas placas condutoras mostradas na figura 8, dado que a placa superior é positiva e a placa inferior tem uma quantidade igual de carga negativa. Certifique-se de que indica a distribuição da carga nas placas. O campo é mais forte onde as placas estão mais próximas? Porque deveria ser?

Figure 8.
- (a) Esboce as linhas do campo eléctrico nas proximidades do isolador carregado na Figura 9. Notar a sua distribuição não uniforme da carga. (b) Esboçar as linhas equipotenciais que rodeiam o isolador. Indicar a direcção do potencial crescente.

Figure 9. Uma haste isolante carregada, tal como pode ser utilizada numa demonstração em sala de aula.
- A carga natural no solo num dia de campo aberto é de -1,00 nC/m2. (a) O que é o campo eléctrico relativamente ao solo a uma altura de 3,00 m? (b) Calcular o potencial eléctrico a esta altura. (c) Esboçar campo eléctrico e linhas equipotenciais para este cenário.
- O raio eléctrico menor (Narcine bancroftii) mantém uma carga incrível na sua cabeça e uma carga igual em magnitude mas oposta em sinal na sua cauda (Figura 10). (a) Esboçar as linhas equipotenciais que rodeiam o raio. (b) Esboçar os equipotenciais quando o raio está próximo de um navio com uma superfície condutora. (c) Como poderia esta distribuição de carga ser útil ao raio?

Figure 10. Raio eléctrico menor (Narcine bancroftii) (crédito: National Oceanic and Atmospheric Administration, NOAA’s Fisheries Collection).
Glossary
linhaequipotencial: uma linha ao longo da qual o potencial eléctrico é constante
terra: fixando um condutor a zero volts ligando-o à terra ou à terra