A função de passo Heaviside é uma função matemática denotada 
, ou por vezes 
ou 
(Abramowitz e Stegun 1972, p. 1020), e também conhecida como a “função de passo de unidade”. O termo “Heaviside step function” e o seu símbolo pode representar tanto uma função de constante de unidades como uma função generalizada.
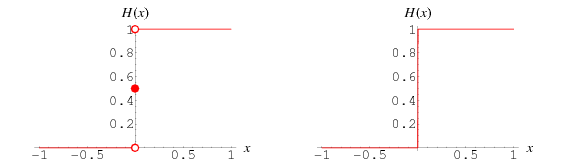
Quando definida como uma função de constante composta, a função de passos de Heaviside é dada por
 |
(1)
|
(Abramowitz e Stegun 1972, p. 1020; Bracewell 2000, p. 61). O gráfico acima mostra esta função (figura da esquerda), e como ela apareceria se exposta num osciloscópio (figura da direita).
Quando definido como uma função generalizada, pode ser definida como uma função 
tal que
 |
(2)
|
for 
a derivada de uma função suficientemente suave 
que se decompõe suficientemente depressa (Kanwal 1998).
A linguagem Wolfram representa a função generalizada Heaviside como HeavisideTheta, ao mesmo tempo que usa UnitStep para representar a função Piecewise (que, convém notar, adopta a convenção 
em vez da definição convencional 
).
A notação abreviada
 |
(3)
|
é por vezes também utilizado.
A função de passo Heaviside está relacionada com a função boxcarfunction por
 |
(4)
|
e pode ser definido em termos da função de sinal por
 |
(5)
|
A derivada de a função de passo é dada por
 |
(6)
|
where 
é a função delta (Bracewell 2000, p. 97).
A função degrau Heaviside está relacionada com a função rampa 
by
 |
(7)
|
e à derivada de 
by
 |
(8)
|
Os dois estão também ligados através de
 |
(9)
|
where 
denota convolução.
Bracewell (2000) dá muitas identidades, algumas das quais incluem o seguinte. Letting 
denota a convolução,
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
Além disso,
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
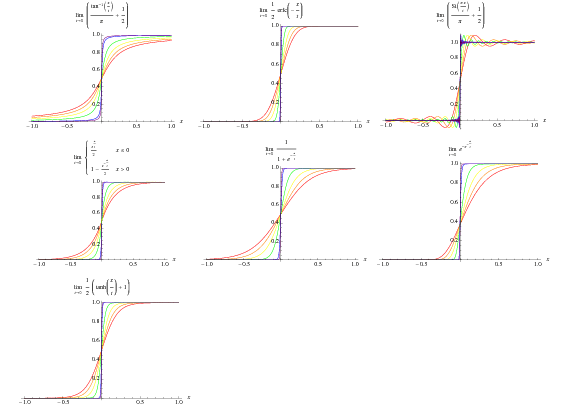
A função de passos Heaviside pode ser definida pelos seguintes limites,
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
 |
 |
 |
(21)
|
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
 |
 |
 |
(25)
|
 |
 |
 |
(26)
|
 |
 |
 |
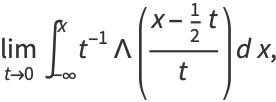(27)
|
where 
é a função erfc, 
é o seno integral, 
é a função sincera, e 
é a função triangular de um só documento. Os primeiros quatro destes são ilustrados acima para 
, 0,1, e 0,01.
Obviamente, qualquer função monotónica com assimetrias horizontais constantes e desiguais é uma função de passo Heaviside sob escala apropriada e possível reflexão. A transformação de Fourier da função de passo Heaviside é dada por
 |
 |
(28)
|
|
 |
 |
 |
(29)
|
where 
é a função delta.