Após a leitura deste capítulo, será capaz de fazer o seguinte
- Definir erro aleatório e diferenciá-lo do viés
- Illustrar erro aleatório com exemplos
- Interpretar um p-valor
- Interpretar um intervalo de confiança
- Diferenciar entre erros estatísticos de tipo 1 e tipo 2 e explicar como se aplicam à investigação epidemiológica
- Descrever como o poder estatístico afecta a investigação
Neste capítulo, cobriremos o erro aleatório – de onde ele vem, como lidamos com ele, e o que significa para a epidemiologia.
P>Primeiro e acima de tudo, o erro aleatório não é preconceituoso. O enviesamento é erro sistemático e é coberto em mais pormenor no capítulo 6.
O erro aleatório é apenas o que soa: erros aleatórios nos dados. Todos os dados contêm erros aleatórios, porque nenhum sistema de medição é perfeito. A magnitude dos erros aleatórios depende em parte da escala em que algo é medido (erros nas medições a nível molecular seriam da ordem dos nanómetros, enquanto os erros nas medições da altura humana são provavelmente da ordem de um centímetro ou dois) e em parte da qualidade das ferramentas que estão a ser utilizadas. Os laboratórios de física e química têm escalas altamente precisas e caras que podem medir a massa ao grama, micrograma ou nanograma mais próximo, enquanto que a escala média na casa de banho de alguém é provavelmente precisa dentro de meia libra ou libra.
Para envolver a cabeça em erro aleatório, imagine que está a fazer um bolo que requer 6 colheres de sopa de manteiga. Para obter as 6 colheres de sopa de manteiga (três quartos de um pau, se houver 4 paus numa libra, como é normalmente o caso nos EUA), poderia usar as marcas que aparecem no papel encerado à volta do pau, assumindo que estão alinhadas correctamente. Ou talvez pudesse seguir o método da minha mãe, que é desembrulhar o pau, fazer uma ligeira marca no que parece ser metade do pau, e depois chegar a três quartos por meio de um olho, metade da metade. Ou poderiam usar o meu método, que é o de olhar para a marca dos três quartos desde o início e cortar em fatias. Qualquer um destes métodos de “medição” dar-lhe-á aproximadamente 6 colheres de sopa de manteiga, o que é certamente suficiente para a confecção de um bolo, mas provavelmente não exactamente 3 onças, que é a quantidade de 6 colheres de sopa de manteiga que pesa nos EUA. A medida em que se está ligeiramente acima das 3 onças desta vez e talvez ligeiramente abaixo das 3 onças da próxima vez está a causar erros aleatórios na medição da manteiga. Se sempre subestimar ou sempre sobrestimar, então isso seria um enviesamento – seja como for, as suas medições consistentemente sub ou sobrestimadas conteriam dentro de si erros aleatórios.
Na epidemiologia, por vezes as nossas medições dependem de um humano que não seja o participante do estudo que mede algo sobre ou sobre o participante. Exemplos incluem a altura ou peso medido, pressão sanguínea, ou colesterol sérico. Para alguns destes (por exemplo, peso e colesterol sérico), o erro aleatório infiltra-se nos dados devido ao instrumento utilizado – aqui, uma balança que tem provavelmente uma flutuação de meia libra, ou um ensaio laboratorial com uma margem de erro de alguns miligramas por decilitro. Para outras medições (por exemplo, altura e tensão arterial), o próprio medidor é responsável por qualquer erro aleatório, como no exemplo da manteiga.
No entanto, muitas das nossas medições dependem da auto-relatação do participante. Existem livros e aulas inteiros dedicados à concepção de questionários, e a ciência por detrás de como obter os dados mais precisos das pessoas através de métodos de inquérito é bastante boa. O Pew Research Center oferece um bom tutorial introdutório sobre a concepção de questionários no seu sítio web.
Relatante à nossa discussão aqui, o erro aleatório aparecerá também nos dados do questionário. Para algumas variáveis, haverá menos erros aleatórios do que para outras (por exemplo, a raça auto-reportada é provavelmente bastante exacta), mas ainda assim haverá algum – por exemplo, pessoas a assinalar acidentalmente a caixa errada. Para outras variáveis, haverá mais erros aleatórios (por exemplo, respostas imprecisas a perguntas como, “No último ano, quantas vezes por mês comeu arroz?”). Uma boa pergunta a fazer a si próprio ao considerar a quantidade de erro aleatório que pode estar numa variável derivada de um questionário é: “As pessoas podem dizer-me isto?”. A maior parte das pessoas poderia teoricamente dizer-lhe quanto tempo dormiu na noite passada, mas seria difícil dizer-lhe quanto sono dormiu na mesma noite há um ano atrás. Se lhe dirão ou não, é um assunto diferente e toca em preconceitos (ver capítulo 6). Independentemente disso, o erro aleatório nos dados do questionário aumenta à medida que a probabilidade de as pessoas lhe poderem dizer a resposta diminui.
Quantifying Random Error
Embora possamos – e devamos – trabalhar para minimizar o erro aleatório (utilizando instrumentos de alta qualidade, formando pessoal sobre como fazer medições, concebendo bons questionários, etc.), este nunca poderá ser eliminado por completo. Felizmente, podemos utilizar estatísticas para quantificar os erros aleatórios presentes num estudo. De facto, é para isto que servem as estatísticas. Neste livro, vou cobrir apenas uma pequena fatia do vasto campo das estatísticas: interpretação dos valores p e intervalos de confiança (IC). Em vez de me concentrar em como calculá-los, centrar-me-ei no que significam (e no que não significam). O conhecimento dos valores p e IC é suficiente para permitir uma interpretação precisa dos resultados dos estudos epidemiológicos para estudantes de epidemiologia iniciantes.
valores p
Ao conduzir investigação científica de qualquer tipo, incluindo epidemiologia, começa-se com uma hipótese, que é depois testada à medida que o estudo é conduzido. Por exemplo, se estivermos a estudar a altura média dos estudantes de graduação, a nossa hipótese (geralmente indicada por H1) pode ser que os estudantes do sexo masculino são, em média, mais altos do que os estudantes do sexo feminino. No entanto, para efeitos de teste estatístico, devemos reformular a nossa hipótese como uma hipótese nula. Neste caso, a nossa hipótese nula (geralmente indicada por H0) seria a seguinte:
Realizaríamos então o nosso estudo para testar esta hipótese. Primeiro determinamos a população alvo (estudantes de graduação) e retiramos uma amostra desta população. Medimos então as alturas e os géneros de todos na amostra, e calculamos a altura média entre os homens versus a altura média entre as mulheres. Em seguida, faríamos um teste estatístico para comparar as alturas médias nos 2 grupos. Como temos uma variável contínua (altura) medida em 2 grupos (homens e mulheres), utilizaríamos um teste t, e a estatística t calculada através deste teste teria um valor p correspondente, que é o que realmente nos interessa.
Vamos dizer que no nosso estudo encontramos que os estudantes masculinos têm em média 5 pés 10 polegadas, e entre os estudantes femininos a altura média é de 5 pés 6 polegadas (para uma diferença de 4 polegadas), e calculamos um valor p de 0,04. Isto significa que se realmente não houver diferença na altura média entre estudantes masculinos e estudantes femininos (isto é, se a hipótese nula for verdadeira) e repetirmos o estudo (até ao momento de retirarmos uma nova amostra da população), há 4% de probabilidade de voltarmos a encontrar uma diferença na altura média de 4 polegadas ou mais.
Existem várias implicações que derivam do parágrafo acima. Primeiro, na epidemiologia, calculamos sempre os valores p de 2 caudas. Aqui isto significa simplesmente que a probabilidade de 4% de uma diferença de altura de ≥4 polegadas nada diz sobre qual o grupo mais alto – apenas que um grupo (seja masculino ou feminino) será mais alto, em média, por pelo menos 4 polegadas. Em segundo lugar, os valores de p não fazem sentido se for possível inscrever toda a população no seu estudo. Como exemplo, digamos que a nossa pergunta de investigação diz respeito aos estudantes de Saúde Pública 425 (H425, Fundações de Epidemiologia) durante o período de Inverno de 2020 na Universidade do Estado do Oregon (OSU). Os homens ou mulheres são mais altos nesta população? Como a população é bastante pequena e todos os membros são facilmente identificados, podemos inscrever toda a gente em vez de ter de confiar numa amostra. Ainda haverá erro aleatório na medição da altura, mas já não utilizamos um valor p para a quantificar. Isto porque se repetirmos o estudo, encontraremos exactamente a mesma coisa, uma vez que na realidade medimos todos na população. Os valores P só se aplicam se estivermos a trabalhar com amostras.
Finalmente, note que o valor p descreve a probabilidade dos seus dados, assumindo que a hipótese nula é verdadeira – não descreve a probabilidade de a hipótese nula ser verdadeira, dados os seus dados. Este é um erro de interpretação comum, cometido tanto por leitores principiantes como por leitores seniores de estudos epidemiológicos. O valor p não diz nada sobre a probabilidade de a hipótese nula ser verdadeira (e, portanto, do outro lado, sobre a verdade da sua hipótese real). Pelo contrário, ele quantifica a probabilidade de obter os dados que obteve se a hipótese nula fosse verdadeira. Esta é uma distinção subtil mas muito importante.
Significado Estatístico
O que acontece a seguir? Temos um valor p, que nos diz a hipótese de obter os nossos dados dada a hipótese nula. Mas o que é que isso significa realmente em termos do que concluir sobre os resultados de um estudo? Na saúde pública e investigação clínica, a prática padrão é utilizar a p ≤ 0,05 para indicar o significado estatístico. Por outras palavras, décadas de investigadores neste campo decidiram colectivamente que se a hipótese de cometer um erro do tipo I (mais sobre o que está abaixo) for de 5% ou menos, nós “rejeitaremos a hipótese nula”. Continuando o exemplo da altura a partir de cima, concluiríamos assim que existe uma diferença de altura entre os géneros, pelo menos entre os estudantes universitários. Para valores de p acima de 0,05, “não rejeitamos a hipótese nula”, e em vez disso concluímos que os nossos dados não forneceram qualquer prova de que havia uma diferença de altura entre estudantes universitários masculinos e femininos.
Se p > 0,05, não rejeitamos a hipótese nula. Não aceitamos nunca a hipótese nula porque é muito difícil provar a ausência de algo. “Aceitar” a hipótese nula implica que provámos que não há realmente diferença de altura entre estudantes masculinos e femininos, o que não foi o que aconteceu. Se p > 0,05, significa apenas que não encontrámos provas em oposição à hipótese nula – não que tais provas não existam. Podemos ter obtido uma amostra estranha, podemos ter tido uma amostra demasiado pequena, etc. Há todo um campo de investigação clínica (investigação de eficácia comparativavi) dedicado a mostrar que um tratamento não é melhor ou pior que outro; os métodos do campo são complexos, e os tamanhos de amostra necessários são bastante grandes. Para a maioria dos estudos epidemiológicos, limitamo-nos simplesmente a não rejeitar.
É o p ≤ 0,05 um corte arbitrário? Absolutamente. Vale a pena ter isto em mente, particularmente para valores de p muito próximos deste corte. Será 0,49 realmente assim tão diferente de 0,51? Provavelmente não, mas eles estão em lados opostos dessa linha arbitrária. O tamanho de um valor p depende de 3 coisas: o tamanho da amostra, o tamanho do efeito (é mais fácil rejeitar a hipótese nula se a verdadeira diferença em altura – se medirmos todos na população, e não apenas a nossa amostra – é de 6 polegadas em vez de 2 polegadas), e a consistência dos dados, mais frequentemente medida pelos desvios padrão em torno das alturas médias nos 2 grupos. Assim, um p-valor de 0,51 poderia, quase de certeza, ser reduzido através da simples inscrição de mais pessoas no estudo (isto diz respeito ao poder, que é o inverso do erro de tipo II, discutido abaixo). É importante ter este facto em mente quando se lê estudos.
Testes de significância estatística fazem parte de um ramo da estatística referido como estatística de frequência.ii Embora extremamente comum em epidemiologia e campos relacionados, esta prática não é geralmente considerada como uma ciência ideal, por uma série de razões. Antes de mais, o corte de 0,05 é inteiramente arbitrário,iii e testes rigorosos de significância rejeitariam o nulo para p = 0,049 mas não rejeitariam para p = 0,051, apesar de serem quase idênticos. Em segundo lugar, há muito mais nuances na interpretação dos valores p e intervalos de confiança do que as que abordei neste capítulo.iv Por exemplo, o valor p está realmente a testar todas as hipóteses de análise, e não apenas a hipótese nula, e um grande valor p indica frequentemente apenas que os dados não podem discriminar entre numerosas hipóteses concorrentes. Contudo, uma vez que tanto a saúde pública como a medicina clínica requerem decisões de sim ou não (Devemos gastar recursos nessa campanha de educação para a saúde? Deve este paciente receber este medicamento?), é necessário que haja algum sistema para decidir sim ou não, e os testes de significância estatística são, actualmente, os mesmos. Existem outras formas de quantificar o erro aleatório, e de facto as estatísticas Bayesianas (que em vez de uma resposta de sim ou não produz uma probabilidade de algo acontecer)ii está a tornar-se cada vez mais popular. No entanto, como as estatísticas de frequência e os testes de hipóteses nulas ainda são de longe os métodos mais comuns utilizados na literatura epidemiológica, são o foco deste capítulo.
Erros de Tipo I e Tipo II
Um erro de tipo I (normalmente simbolizado por α, a letra grega alfa, e estreitamente relacionado com os valores p) é a probabilidade de rejeitar incorrectamente a hipótese nula – por outras palavras, de “encontrar” algo que não está realmente lá. Ao escolher 0,05 como o nosso corte de significância estatística, nós nos campos da saúde pública e da investigação clínica concordámos tacitamente que estamos dispostos a aceitar que 5% das nossas descobertas serão realmente erros de tipo I, ou falsos positivos.
Um erro de tipo II (geralmente simbolizado por β, a letra grega beta) é o oposto: β é a probabilidade de não rejeitar incorrectamente a hipótese nula – por outras palavras, de não encontrar algo que realmente existe.
Power em estudos epidemiológicos varia muito: idealmente deveria ser pelo menos 90% (o que significa que a taxa de erro de tipo II é 10%), mas muitas vezes é muito mais baixa. A potência é proporcional ao tamanho da amostra, mas de uma forma exponencial – a potência sobe à medida que o tamanho da amostra aumenta, mas para obter uma potência de 90 a 95% é necessário um salto muito maior no tamanho da amostra do que para passar de 40 a 45% de potência. Se um estudo não rejeitar a hipótese nula, mas os dados parecerem que pode haver uma grande diferença entre grupos, muitas vezes a questão é que o estudo não tinha potência, e com uma amostra maior, o valor p provavelmente cairia abaixo do corte mágico de 0,05. Por outro lado, parte da questão com amostras pequenas é que se poderia, por acaso, ter obtido uma amostra não representativa, e acrescentar participantes adicionais não conduziria os resultados a uma significância estatística. Como exemplo, suponha que estamos novamente interessados nas diferenças de altura baseadas no género, mas desta vez apenas entre os atletas colegiados. Começamos com um estudo muito pequeno – apenas uma equipa de homens e uma equipa de mulheres. Se por acaso escolhermos, digamos, a equipa masculina de basquetebol e a equipa feminina de ginástica, é provável que encontremos uma diferença enorme nas alturas médias – talvez de 18 polegadas ou mais. Adicionar outras equipas ao nosso estudo resultaria quase certamente numa diferença muito mais estreita nas alturas médias, e a diferença de 18 polegadas “encontrada” no nosso pequeno estudo inicial não se aguentaria com o tempo.
Intervalos de Confiança
Porque fixámos o nível aceitável \alfa em 5%, em epidemiologia e campos relacionados, usamos mais frequentemente intervalos de confiança de 95% (95% CI). Pode-se usar um IC 95% para fazer testes de significância: se o IC 95% não incluir o valor nulo (0 para diferença de risco e 1,0 para odds ratios, rácios de risco, e rate ratios), então p < 0.05, e o resultado é estatisticamente significativo.
P>Possuindo 95% CI pode ser usado para testes de significância, contêm muito mais informação do que apenas se o valor p é <0.05 ou não. A maioria dos estudos epidemiológicos relatam 95% de IC em torno de quaisquer estimativas pontuais que são apresentadas. A interpretação correcta de um IC 95% é a seguinte:
Podemos também ilustrar isto visualmente:
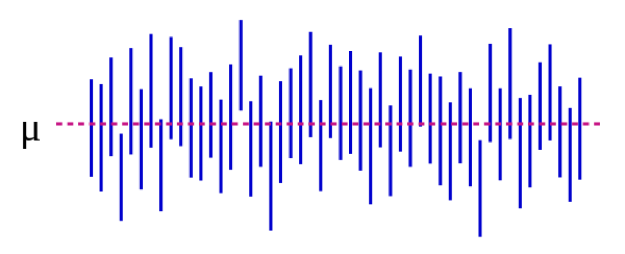
Source: https://es.wikipedia.org/wiki/Intervalo_de_confianza
Na Figura 5-1, o parâmetro da população μ representa a resposta “real” que obteria se pudesse inscrever absolutamente toda a população no estudo. Estimamos μ com dados da nossa amostra. Continuando com o nosso exemplo de altura, isto poderia ser 5 polegadas: se pudéssemos medir magicamente as alturas de cada estudante universitário nos EUA (ou no mundo, dependendo de como se define a população alvo), a diferença média entre estudantes do sexo masculino e feminino seria de 5 polegadas. É importante notar que este parâmetro de população é quase sempre inobservável – só se torna observável se definirmos a nossa população de forma suficientemente restrita para podermos inscrever todos. Cada linha vertical azul representa o IC de um “estudo” individual -50 deles, neste caso. Os IC variam porque a amostra é ligeiramente diferente de cada vez – de facto, a maioria dos IC (todos excepto 3) contém μ.
Se realizarmos o nosso estudo e encontrarmos uma diferença média de 4 polegadas (95% CI, 1,5 – 7), o IC diz-nos 2 coisas. Primeiro, o valor p para o nosso teste t seria <0,05, uma vez que o IC exclui 0 (o valor nulo neste caso, uma vez que estamos a calcular uma medida de diferença). Em segundo lugar, a interpretação do IC é: se repetirmos o nosso estudo (incluindo o desenho de uma nova amostra) 100 vezes, então 95 dessas vezes o nosso IC incluiria o valor real (que sabemos aqui ser de 5 polegadas, mas que na vida real não se saberia). Assim, olhando para o IC aqui de 1,5 – 7,0 polegadas dá uma ideia do que a diferença real pode ser – quase de certeza que está algures dentro desse intervalo mas pode ser tão pequena quanto 1,5 polegadas ou tão grande quanto 7 polegadas. Tal como os p-valores, as IC dependem do tamanho da amostra. Uma amostra grande produzirá um IC comparativamente mais estreito. Os IC mais estreitos são considerados melhores porque produzem uma estimativa mais precisa do que a resposta “verdadeira” poderá ser.
Sumário
O erro aleatório está presente em todas as medições, embora algumas variáveis sejam mais propensas a ele do que outras. Os valores P e CIs são utilizados para quantificar o erro aleatório. Um p-valor de 0,05 ou menos é geralmente considerado como “estatisticamente significativo”, e o IC correspondente excluiria o valor nulo. Os IC são úteis para expressar o intervalo potencial do valor “real” a nível populacional que está a ser estimado.
i. Manteiga nos EUA e no resto do mundo. Cozinha dos Erros. Março de 2014. https://www.errenskitchen.com/cooking-conversions/butter-measurement-weight-conversions/. Acedido a 26 de Setembro de 2018. (↵ Voltar)
ii. Abordagem Bayesiana vs frequentista: mesmos dados, resultados opostos. 365 Data Sci. Agosto 2017. https://365datascience.com/bayesian-vs-frequentist-approach/. Acedido a 17 de Outubro de 2018. (↵ Voltar 1) (↵ Voltar 2)
iii. Smith RJ. O uso indevido contínuo de testes de significância de hipóteses nulas em antropologia biológica. Am J Antropol Físico. 2018;166(1):236-245. doi:10.1002/ajpa.23399 (↵ Return)
iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. P-valores e saúde reprodutiva: o que podem os investigadores clínicos aprender com a Associação Americana de Estatística? Hum Reprod Oxf Engl. 2016;31(11):2406-2410. doi:10.1093/humrep/dew192 (↵ Return)
v. Greenland S, Senn SJ, Rothman KJ, et al. Testes estatísticos, valores p, intervalos de confiança, e poder: um guia para interpretações erradas. Eur J Epidemiol. 2016;31:337-350. doi:10.1007/s10654-016-0149-3
vi. Porque é importante a investigação de eficácia comparativa? Instituto de Investigação de Resultados Centrados no Paciente. https://www.pcori.org/files/why-comparative-effectiveness-research-important. Acedido a 17 de Outubro de 2018. (↵ Return)
- Não existe apenas uma fórmula para calcular um valor p ou um IC. Em vez disso, as fórmulas mudam consoante o teste estatístico que está a ser aplicado. Qualquer texto introdutório de bioestatística que discuta quais os métodos estatísticos a utilizar e quando forneceria também a informação correspondente sobre o valor p e o cálculo de IC. ↵
- Como escolher o teste correcto está para além do âmbito deste livro – ver qualquer livro sobre bioestatística introdutória ↵
li>Não demore muito tempo a tentar perceber porque precisamos de uma hipótese nula; apenas o fazemos. A lógica está enterrada em séculos de filosofia académica de argumentos científicos. ↵
Inherente em todas as medições. “Ruído” nos dados. Estará sempre presente, mas a quantidade depende da precisão dos seus instrumentos de medição. Por exemplo, as balanças de casa de banho têm normalmente 0,5 – 1 libra de erro aleatório; os laboratórios de física contêm frequentemente balanças que têm apenas alguns microgramas de erro aleatório (estas são mais caras, e só podem pesar pequenas quantidades). É possível reduzir a quantidade pela qual o erro aleatório afecta os resultados do estudo, aumentando o tamanho da amostra. Isto não elimina o erro aleatório, mas permite melhor que o investigador veja os dados dentro do ruído. Corolário: aumentar o tamanho da amostra diminuirá o valor p, e reduzirá o intervalo de confiança, uma vez que estas são formas de quantificar o erro aleatório.
Systematic error. O enviesamento de selecção deriva de uma amostragem deficiente (a sua amostra não é representativa da população alvo), uma taxa de resposta deficiente por parte dos convidados a estar num estudo, tratando casos e controlos ou expostos/unexpostos de forma diferente, e/ou uma perda desigual para o seguimento entre grupos. Para avaliar o enviesamento de selecção, pergunte-se “quem obtiveram, e quem falharam?” – e depois pergunte-se também “será que isso importa”? Às vezes importa, outras vezes, talvez não.
P>Posicionamento de classificação errada significa que algo (ou a exposição, o resultado, um confundidor, ou todos os três) foi medido de forma imprópria. Exemplos incluem pessoas que não são capazes de lhe dizer algo, pessoas que não estão dispostas a dizer algo, e uma medida objectiva que é de alguma forma sistematicamente errada (por exemplo, sempre na mesma direcção, como uma manga de tensão arterial que não é zerada correctamente). Enviesamento de recordação, enviesamento de desejo social, enviesamento de entrevistador – estes são todos exemplos de enviesamento de classificação errada. O resultado final de todos eles é que as pessoas são colocadas na caixa errada numa tabela 2×2. Se a classificação errada for igualmente distribuída entre os grupos (por exemplo, tanto os expostos como os não expostos têm igual hipótese de serem colocados na caixa errada), é uma classificação errada não-diferencial. Caso contrário, é uma classificação errada diferencial.
Uma forma de quantificar o erro aleatório. A interpretação correcta de um valor p é: a probabilidade de que, se repetisse o estudo (voltar à população alvo, retirar uma nova amostra, medir tudo, fazer a análise), encontraria um resultado pelo menos tão extremo, assumindo que a hipótese nula é verdadeira. Se for realmente verdade que não há diferença entre os grupos, mas o seu estudo descobriu que havia mais 15% de fumadores no grupo A com um valor p de 0,06, então isso significa que há uma probabilidade de 6% de que, se repetisse o estudo, encontraria novamente 15% (ou um número maior) de fumadores num dos grupos. Na saúde pública e investigação clínica, utilizamos normalmente um corte de p < 0,05 para significar “estatisticamente significativo”- assim, estamos a permitir uma taxa de erro de tipo I de 5%. Assim, 5% do tempo vamos “encontrar” algo, mesmo que realmente não haja uma diferença (ou seja, mesmo que realmente a hipótese nula seja verdadeira). Os outros 95% do tempo, estamos a rejeitar correctamente a hipótese nula e a concluir que existe uma diferença entre os grupos.
Uma forma de quantificar o erro aleatório. A interpretação correcta de um intervalo de confiança é: se repetir o estudo 100 vezes (voltar à sua população alvo, obter uma nova amostra, medir tudo, fazer a análise), então 95 das 100 vezes o intervalo de confiança que calcula como parte deste processo incluirá o valor verdadeiro, assumindo que o estudo não contém qualquer enviesamento. Aqui, o valor verdadeiro é aquele que obteria se conseguisse inscrever todos da população no seu estudo – isto quase nunca é realmente observável, uma vez que as populações são normalmente demasiado grandes para ter todos incluídos numa amostra. Corolário: Se a sua população for suficientemente pequena para que possa ter todos no seu estudo, então o cálculo de um intervalo de confiança é discutível.
Used in statistical significance testing. A hipótese nula é sempre que não há diferença entre os dois grupos em estudo.
Um teste estatístico que determina se os valores médios em dois grupos são diferentes.
Um método um pouco arbitrário para determinar se deve ou não acreditar nos resultados de um estudo. Na investigação clínica e epidemiológica, o significado estatístico é tipicamente fixado em p < 0,05, significando uma taxa de erro de tipo I de <5%. Como com todos os métodos estatísticos, diz respeito apenas ao erro aleatório; um estudo pode ser estatisticamente significativo mas não credível, por exemplo, se houver probabilidade de enviesamento substancial. Um estudo também pode ser estatisticamente significativo (por exemplo, p era < 0,05) mas não clinicamente significativo (por exemplo, se a diferença na tensão arterial sistólica entre os dois grupos fosse de 2 mm Hg – com uma amostra suficientemente grande isto seria estatisticamente significativo, mas não importa de todo clinicamente).
A probabilidade de um estudo “encontrar” algo que não existe. Tipicamente representado por α, e intimamente relacionado com os valores p. Normalmente fixado em 0,05 para estudos clínicos e epidemiológicos.
A probabilidade de que o seu estudo “encontre” algo que não esteja lá. Power = 1 – β; beta é a taxa de erro do tipo II. Pequenos estudos, ou estudos de eventos raros, são tipicamente pouco potentes.
A probabilidade de um estudo não ter encontrado algo que lá estivesse. Tipicamente representado por β, e intimamente relacionado com o poder. O ideal será estar acima dos 90% para estudos clínicos e epidemiológicos, embora na prática isto muitas vezes não aconteça.
A medida de associação que é calculada num estudo. Tipicamente apresentado com um intervalo de confiança correspondente a 95%.