>div>
>h2>Bases de representação gráfica Funções exponenciais
A função exponencial y=b^x onde b>0 é uma função que permanecerá proporcional ao seu valor original quando cresce ou se decompõe.
Objectivos de aprendizagem
Descrever as propriedades dos gráficos de funções exponenciais
Key Takeaways
Key Points
- Se a base, b, for superior a 1, então a função aumenta exponencialmente a uma taxa de crescimento de b. Isto é conhecido como crescimento exponencial.
- Se a base, b, for inferior a 1 (mas superior a 0) a função diminui exponencialmente a uma taxa de b. Isto é conhecido como decadência exponencial.
- Se a base, b, for igual a 1, então a função trivialmente torna-se y=a.
- Os pontos (0,1) e (1,b) estão sempre no gráfico da função y=b^x
- A função y=b^x assume apenas valores positivos e tem o eixo x como uma assímptota horizontal.
- crescimento exponencial: O crescimento no valor de uma quantidade, em que a taxa de crescimento é proporcional ao valor instantâneo da quantidade; por exemplo, quando o valor duplicou, a taxa de crescimento também terá duplicado. A taxa pode ser positiva ou negativa. Se negativa, é também conhecida como decadência exponencial.
- assímptota: Uma linha que uma curva se aproxima arbitrariamente de perto. Uma assímptota pode ser vertical, oblíqua ou horizontal. As assímptotas horizontais correspondem ao valor de aproximação da curva à medida que x fica muito grande ou muito pequena.
- função exponencial: Qualquer função na qual uma variável independente tem a forma de expoente; são as funções inversas de logaritmos.
Key Terms
Definições
No nível mais básico, uma função exponencial é uma função na qual a variável aparece no expoente. A função exponencial mais básica é uma função da forma y=b^x onde b é um número positivo.
Quando b>1 a função cresce de uma forma proporcional ao seu valor original. Isto é chamado crescimento exponencial.
Quando 0>b>1 a função decresce de uma forma que é proporcional ao seu valor original. A isto chama-se decadência exponencial.
Grafar uma Função Exponencial
Deixe-nos considerar a função y=2^x quando b>1. Uma forma de grafar esta função é escolher valores para x e substituí-los na equação para gerar valores para y. Ao fazê-lo, podemos obter os seguintes pontos:
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) e (2,4)
Ao ligar os pontos, notar-se-á uma curva suave que atravessa o eixo y no ponto (0,1) e aumenta à medida que x assume valores cada vez maiores. Ou seja, a curva aproxima-se do infinito à medida que x se aproxima do infinito. À medida que x assume valores cada vez menores, a curva aproxima-se cada vez mais do eixo x. Ou seja, a curva aproxima-se de zero à medida que x se aproxima do infinito negativo fazendo com que o eixo x seja uma assímptota horizontal da função. O ponto (1,b) está no gráfico. Isto é verdade no gráfico de todas as funções exponenciais da forma y=b^x para x>1,

gráfico de y=2^x: O gráfico desta função atravessa o eixo y a (0,1) e aumenta à medida que x se aproxima do infinito. O eixo x é uma assímptota horizontal da função.
Exemplo 2
Deixe-nos considerar a função y=\frac{1}{2}^x quando 0<b<1. Uma forma de grafar esta função é escolher valores para x e substituí-los na equação para gerar valores para y. Ao fazê-lo, pode obter os seguintes pontos:
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) e (2,\frac{1}{4})
Ao ligar os pontos, notará uma curva suave que atravessa o eixo y no ponto (0,1) e está a diminuir à medida que x assume valores cada vez maiores. A curva aproxima-se do infinito zero à medida que se aproxima do infinito. medida que x assume valores cada vez mais pequenos, a curva aproxima-se cada vez mais do eixo x. Ou seja, a curva aproxima-se do zero à medida que x se aproxima do infinito negativo fazendo do eixo x uma assímptota horizontal da função. O ponto (1,b) está no gráfico. Isto é verdade para o gráfico de todas as funções exponenciais da forma y=b^x para 0<x<1.
Como se pode ver no gráfico abaixo, o gráfico de y=\frac{1}{2}^x é simétrico ao de y=2^x sobre o eixo y. Ou seja, se o plano fosse dobrado sobre o eixo y, as duas curvas estariam uma sobre a outra.
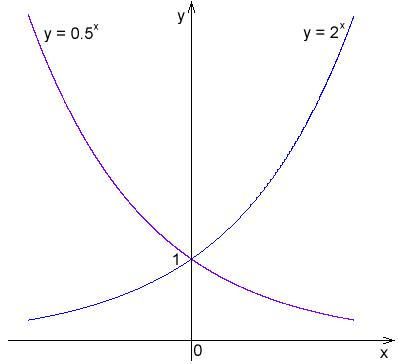
Gráfico de y=2^x e y=\frac{1}{2}^x: Os gráficos destas funções são simétricos sobre o eixo y.
Porquê b deve ser um número positivo?
Se b=1, então a função torna-se y=1^x. Como 1 para qualquer potência 1, a função é equivalente a y=1 que é uma linha horizontal, não uma equação exponencial.
Se b for negativo, então elevar b para uma potência par resulta num valor positivo para y enquanto que elevar b para uma potência ímpar resulta num valor negativo para y, tornando impossível juntar os pontos obtidos de uma forma significativa e certamente não de uma forma que gere uma curva como os dos exemplos acima.
Propriedades de Gráficos Exponenciais
O ponto (0,1) está sempre no gráfico de uma função exponencial da forma y=b^x porque b é positivo e qualquer número positivo para os rendimentos de potência zero 1.
O ponto (1,b) está sempre no gráfico de uma função exponencial da forma y=b^x porque qualquer número positivo b elevado à primeira potência 1,
A função y=b^x assume apenas valores positivos porque qualquer número positivo b irá render apenas valores positivos quando elevado a qualquer potência.
A função y=b^x tem o eixo x como uma assímptota horizontal porque a curva aproximar-se-á sempre do eixo x à medida que x se aproxima do infinito positivo ou negativo, mas nunca atravessará o eixo porque nunca será igual a zero.
Gráficos de funções logarítmicas
Funções logarítmicas podem ser agarradas manualmente ou electronicamente com pontos geralmente determinados através de uma calculadora ou tabela.
Objectivos de aprendizagem
Descrever as propriedades dos gráficos das funções logarítmicas
Requisitos-chave
Pontos-chave
- Quando se grava, a função logarítmica é semelhante em forma à função da raiz quadrada, mas com uma assímptota vertical à medida que x se aproxima de 0 a partir da direita.
- O ponto (1,0) está no gráfico de todas as funções logarítmicas da forma y=log{_b}x, onde b é um número real positivo.
- O domínio da função logarítmica y=log{_b}x, onde b é todos os números reais positivos, é o conjunto de todos os números reais positivos, enquanto o intervalo desta função é todos os números reais.
- O gráfico de uma função logarítmica do formulário y=log{_b}x pode ser deslocado horizontalmente e/ou verticalmente adicionando uma constante à variável x ou a y, respectivamente.
- Uma função logarítmica do formulário y=log{_b}x em que b é um número real positivo, pode ser grapado usando uma calculadora para determinar pontos no gráfico ou pode ser grapado sem uma calculadora usando o facto de que o seu inverso é uma função exponencial.
Key Terms
- função logarítmica: Qualquer função na qual uma variável independente aparece sob a forma de logaritmo. O inverso de uma função logarítmica é uma função exponencial e vice versa.
- logaritmo: O logaritmo de um número é o expoente pelo qual outro valor fixo, a base, tem de ser elevado para produzir esse número.
- asymptote: Uma linha que uma curva se aproxima arbitrariamente de perto. As assímptotas podem ser horizontais, verticais ou oblíquas.
Below são gráficos de funções logarítmicas com bases 2, e, e, e 10.
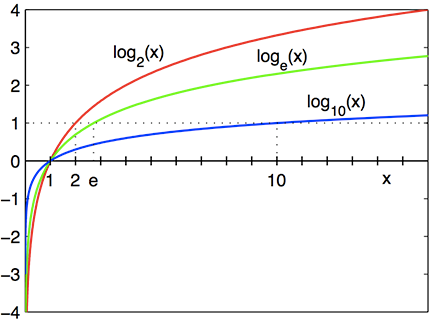
Gráficos logarítmicos: Depois de x=1, onde os gráficos cruzam o eixo x, \log_2(x) em vermelho está acima de \log_e(x) em verde, que está acima de \log_{10}(x) em azul. Antes deste ponto, a ordem é invertida. Todos os três logaritmos têm o eixo y como assíntota vertical, e estão sempre a aumentar.
Todos os três logaritmos começam com uma subida íngreme depois de x=0, mas esticam-se cada vez mais horizontalmente, a sua inclinação sempre a diminuir à medida que x aumenta. Todos eles atravessam o eixo x a x=1,
Propriedades dos gráficos de funções logarítmicas
O gráfico atravessa o eixo x a 1, ou seja, o gráfico tem uma interpretação x de 1, e como tal, o ponto (1,0) está no gráfico. De facto, o ponto (1,0) estará sempre no gráfico de uma função da forma y=log{_b}x onde b>0. Isto porque para x=1, a equação do gráfico torna-se y=log{_b}1.
Thus, estamos à procura de um expoente y tal que b^y=1. Como b>0, o expoente que procuramos é 1 independentemente do valor de b. Isto significa que o ponto (x,y)=(1,0) estará sempre numa função logarítmica deste tipo.
Asymptotes
O eixo y é uma assímptota vertical do gráfico. Isto significa que a curva se aproxima cada vez mais do eixo y mas não o atravessa.
Deixe-nos considerar o que acontece quando o valor de x se aproxima de zero da direita para a equação cujo gráfico aparece acima. Nomeadamente, y=log{_b}x. Podemos fazer isto escolhendo valores para x, ligando-os à equação e gerando valores para y.
Deixe-nos assumir que b é um número positivo superior a 1, e deixe-nos investigar valores de x entre 0 e 1. Nestas condições, se deixarmos x=\frac{1}{b}, a equação torna-se y=log\frac{1}{b}.
P>Assim, estamos à procura de um expoente tal que b elevado a esse expoente produz \frac{1}{b}. O expoente que procuramos é -1 e o ponto (\frac{1}{b},-1) está no gráfico. Da mesma forma, podemos obter os seguintes pontos que também estão no gráfico:
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) e assim por diante
Se tomarmos valores de x que estejam ainda mais próximos de 0, podemos chegar aos pontos seguintes: (\frac{1}{b^{10},-10),(\frac{1}{b^{100}},-100) e (\frac{1}{b^{1000},-1000)
Como se pode ver, quanto mais próximo de 0 se aproxima o valor de x, mais e mais negativo se torna o gráfico. Ou seja, à medida que x se aproxima de zero, o gráfico aproxima-se do infinito negativo. Isto significa que o eixo y é uma assímptota vertical da função.
Domínio e Alcance
O domínio da função é todo de números positivos. Isto significa que o valor x da função será sempre positivo. Comecemos por considerar porque é que o valor x da curva nunca é 0,
Se o valor x fosse zero, a função leria y=log{_b}0,
Aqui estamos à procura de um expoente tal que b elevado a esse expoente é 0. Uma vez que b é um número positivo, não há expoente a que possamos elevar b de modo a obter 0. De facto, uma vez que b é positivo, elevá-lo para uma potência produzirá sempre um número positivo.
O alcance da função é todo de números reais. Ou seja, o gráfico pode assumir qualquer número real.
Comparando y=log{_x} e y=\sqrt{x}
à primeira vista, o gráfico da função logarítmica pode ser facilmente confundido com o da função da raiz quadrada.
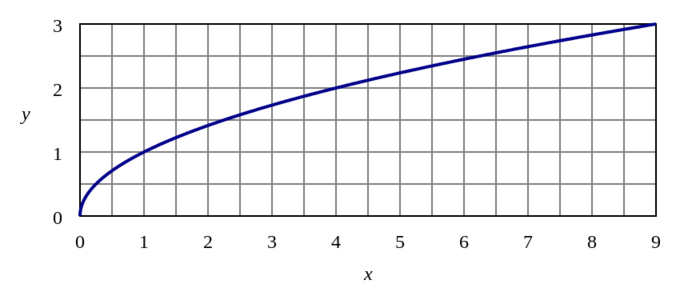
Gráfico de y=\sqrt{x}: O gráfico da função da raiz quadrada assemelha-se ao gráfico da função logarítmica, mas não tem uma assímptota vertical.
Bambas as funções da raiz quadrada e logarítmica têm um domínio limitado a valores x superiores a 0. No entanto, a função logarítmica tem uma assímptota vertical descendente em direcção a -\i>, à medida que x se aproxima de 0, enquanto que a raiz quadrada atinge um valor y mínimo de 0. O intervalo da função da raiz quadrada é todo de números reais não negativos, enquanto que o intervalo da função logarítmica é todo de números reais.
Grafar funções logarítmicas
Grafar funções logarítmicas pode ser feito localizando pontos na curva quer manualmente quer com uma calculadora.
Quando se grafa sem calculadora, utilizamos o facto de que o inverso de uma função logarítmica é uma função exponencial.
Quando fazemos gráficos com uma calculadora, utilizamos o facto de que a calculadora só pode calcular logaritmos comuns (base é 10), logaritmos naturais (base é e) ou logaritmos binários (base é 2). Claro que, se tivermos uma calculadora gráfica, a calculadora pode grafar a função sem a necessidade de encontrarmos pontos no gráfico.
Grafar funções logarítmicas usando os seus Inversos
Funções logarítmicas podem ser grafadas à mão sem o uso de uma calculadora se usarmos o facto de que são inversos de funções exponenciais.
Deixe-nos novamente considerar o gráfico da seguinte função:
y=log{_3}x
p>Esta pode ser escrita de forma exponencial como:
3^y=x
P>Agora consideremos o inverso desta função. Para tal, trocamos x e y:
3^x=y
A função exponencial 3^x=y é uma função para a qual podemos facilmente gerar pontos. Se tomarmos alguns valores para x e os ligarmos à equação para encontrar os valores correspondentes para y, podemos obter os seguintes pontos:
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) e (3,27)
p>Agora temos de notar que estes pontos não estão na função original (y=log{_3}x) mas sim no seu inverso 3^x=y. Contudo, se trocarmos as coordenadas x e y de cada ponto, obteremos de facto uma lista de pontos sobre a função original.
Estes são: (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) e (27,3).
Traçamos e ligamos estes pontos para obter o gráfico da função y=log{_3}x abaixo.

gráfico de y=log{_3}x: O gráfico da função logarítmica com base 3 pode ser gerado usando o inverso da função. A sua forma é a mesma de outras funções logarítmicas, apenas com uma escala diferente.
Gráfico de funções logarítmicas com bases entre 0 e 1
Até aqui temos grafadas funções logarítmicas cujas bases são superiores a 1. Se em vez disso considerarmos funções logarítmicas com uma base b, tal que 0<b<1, obtemos um gráfico que é muito semelhante aos que já vimos.
De facto, se b>0, o gráfico de y=log{_b}x e o gráfico de y=log{_frac{_1}{b}}x são simétricos sobre o eixo x. Assim, se identificarmos um ponto (x,y) no gráfico de y=log{_b}x, podemos encontrar o ponto correspondente em y=log{_\frac{1}{b}}x, alterando o sinal da coordenada y. O ponto correspondente é (x,-y).
Aqui está um exemplo para b=2.
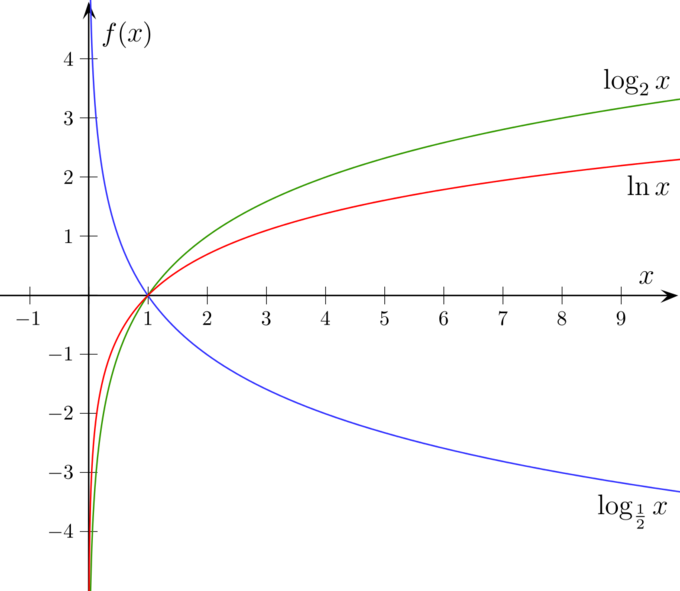
Gráficos de log{_2}x e log{_\frac{1}{2}x : Os gráficos de log_2 x e log{_\frac{1}{2}x são simétricos sobre o eixo x
Solucionar problemas com gráficos logarítmicos
Algumas funções com forma em rápida mudança são melhor plotadas numa escala que aumenta exponencialmente, tal como um gráfico logarítmico.
Objectivos de aprendizagem
Problemas de conversão para escalas logarítmicas e discutir as vantagens de o fazer
Realizar pontos-chave
Pontos-chave
- Gráficos logarítmicos usam escalas logarítmicas, nas quais os valores diferem exponencialmente. Por exemplo, em vez de incluir marcas a 0,1,2 e 3, uma escala logarítmica pode incluir marcas a 0,1, 1, 10 e 100, cada uma a uma distância igual da anterior e da seguinte.
- Gráficos logarítmicos permitem traçar uma gama muito grande de dados sem perder a forma do gráfico.
- Gráficos logarítmicos facilitam a interpolação em áreas que podem ser difíceis de ler em eixos lineares. Por exemplo, se o gráfico y=x^5 for escalado para mostrar uma gama muito ampla de valores y, a curvatura perto da origem pode ser indistinguível em eixos lineares. É muito mais claro nos eixos logarítmicos.
Key Terms
- logaritmo: O logaritmo de um número é o expoente pelo qual outro valor fixo, a base, tem de ser elevado para produzir esse número.
- interpolar: Para estimar o valor de uma função entre dois pontos entre os quais é tabelado.
Porquê Utilizar uma Escala Logarítmica?
Muitas relações matemáticas e físicas são funcionalmente dependentes de variáveis de alta ordem. Isto significa que para pequenas alterações na variável independente há alterações muito grandes na variável dependente. Assim, torna-se difícil graficar tais funções no eixo padrão.
Considerar, como exemplo, a lei Stefan-Boltzmann, que relaciona a potência (j*) emitida por um corpo negro com a temperatura (T).
j^*= \sigma T^4
Num gráfico padrão, esta equação pode ser bastante pesada. A dependência do quarto grau da temperatura significa que a potência aumenta extremamente rapidamente. O facto de a taxa estar sempre a aumentar (e acentuadamente) significa que a mudança de escala (escala dos eixos em 5, 10 ou mesmo 100) é de pouca ajuda para tornar o gráfico mais fácil de interpretar.
Para funções muito íngremes, é possível traçar pontos de forma mais suave, mantendo a integridade dos dados: pode-se usar um gráfico com uma escala logarítmica, onde em vez de cada espaço num gráfico representando um aumento constante, representa um aumento exponencial. Onde um gráfico normal (linear) pode ter intervalos iguais que vão 1, 2, 3, 4, uma escala logarítmica teria esses mesmos intervalos iguais que representam 1, 10, 100, 1000. Aqui estão alguns exemplos de funções grafadas numa escala linear, semi-log e escalas logarítmicas.
A parte superior esquerda é uma escala linear. A parte inferior direita é uma escala logarítmica. A superior direita e a inferior esquerda são chamadas escalas semi-logares porque um eixo é escalado linearmente enquanto o outro é escalado utilizando logaritmos.

Escala logarítmica: Os gráficos das funções f(x)=10^x,f(x)=x e f(x)=\log x em quatro parcelas de coordenadas diferentes. Top Left é uma escala linear, top right e bottom left são escalas semi-logares e bottom right é uma escala logarítmica.
Como se pode ver, quando ambos os eixos usaram uma escala logarítmica (bottom right) o gráfico manteve as propriedades do gráfico original (top left) onde ambos os eixos foram escalados usando uma escala linear. Isto significa que se quisermos fazer um gráfico de uma função que não seja de fácil utilização numa escala linear, podemos utilizar uma escala logarítmica em cada eixo e reter as propriedades do gráfico, ao mesmo tempo que se torna mais fácil fazer o gráfico.
Com as escalas de semi-log, as funções têm formas que são enviesadas em relação ao original. Quando apenas o eixo x tem uma escala logarítmica, a curva logarítmica aparece como uma linha e as curvas linear e exponencial parecem ambas exponenciais. Quando apenas o eixo y tem uma escala logarítmica, a curva exponencial aparece como uma linha e as curvas lineares e logarítmicas aparecem ambas logarítmicas. É de notar que os exemplos nos gráficos foram feitos para ilustrar um ponto e que as funções grafadas não eram necessariamente pesadas num conjunto de escalas lineares de eixos.
Converter escalas lineares para logarítmicas
A diferença primária entre as escalas logarítmicas e lineares é que, enquanto a diferença de valor entre pontos lineares de igual distância permanece constante (isto é, se o espaço de 0 a 1 na escala for de 1 cm na página, a distância de 1 a 2, 2 a 3, etc.), será a mesma), a diferença de valor entre pontos de uma escala logarítmica mudará exponencialmente. Uma escala logarítmica começará com uma determinada potência de 10, e com cada unidade aumentará com uma potência de 10,
Assim, se se quisesse converter uma escala linear (com valores 0-5 para uma escala logarítmica, uma opção seria substituir 1,2,3,4 e 5 por 0,001,0,01,0,1,1,10 e 100, respectivamente. Entre cada valor principal na escala logarítmica, as hashmarks tornam-se cada vez mais próximas, juntamente com o aumento do valor. Por exemplo, no espaço entre 1 e 10, os 8 e 9 estão muito mais próximos entre si do que os 2 e 3,
As vantagens de utilizar uma escala logarítmica são duas vezes maiores. Em primeiro lugar, ao fazê-lo, permite traçar uma gama muito grande de dados sem perder a forma do gráfico. Em segundo lugar, permite interpolar em qualquer ponto da parcela, independentemente do alcance do gráfico. Dados semelhantes traçados numa escala linear são menos claros.
Solucionar problemas usando gráficos logarítmicos
Um ponto-chave sobre a utilização de gráficos logarítmicos para resolver problemas é que eles expandem escalas até ao ponto em que grandes gamas de dados fazem mais sentido. Na equação acima mencionada (j^*= \sigma T^4), o traçado j vs. T geraria a curva esperada, mas a escala seria tal que as mudanças minúsculas passariam despercebidas e os efeitos em grande escala da relação dominariam o gráfico: É tão grande que as “áreas interessantes” não cabem no papel numa escala legível.
Tomando o logaritmo de cada lado das equações produz-se: logj=log{(\sigma\tau ) }^4 . Confiamos agora nas propriedades dos logaritmos para reescrever a equação.
Recall the following properties of logarithms:
\log(ab)=\log(a)+\log(b) \log(a)^b=(b)^log(a)
p>Usando o acima exposto, a nossa equação torna-se:p>begin{align} j&=4\log{(\sigma\tau}} {(\sigma\tau}} \\&=4\log{(\sigma)}+4\log{(\tau}} \\&=4\log{(\tau ) }+4\log{(\sigma)} \end{align}