Obiettivi di apprendimento
Al termine di questa sezione, sarete in grado di:
- spiegare uno scenario in cui il campo magnetico e quello elettrico si incrociano e le loro forze si bilanciano a vicenda mentre una particella carica si muove attraverso un selettore di velocità
- Confrontare come si muovono i portatori di carica in un materiale conduttivo e spiegare come questo si collega all’effetto Hall
Nel 1879, E.H. Hall ideò un esperimento che può essere usato per identificare il segno dei portatori di carica predominanti in un materiale conduttore. Da un punto di vista storico, questo esperimento fu il primo a dimostrare che i portatori di carica nella maggior parte dei metalli sono negativi.
Visita questo sito web per trovare maggiori informazioni sull’effetto Hall.
Indaghiamo l’effetto Hall studiando il moto degli elettroni liberi lungo una striscia metallica di larghezza l in un campo magnetico costante (Figura \(\PageIndex{1}}). Gli elettroni si muovono da sinistra a destra, quindi la forza magnetica che sperimentano li spinge verso il bordo inferiore della striscia. Questo lascia un eccesso di carica positiva sul bordo superiore della striscia, con un conseguente campo elettrico E diretto dall’alto verso il basso. La concentrazione di carica su entrambi i bordi si accumula finché la forza elettrica sugli elettroni in una direzione è bilanciata dalla forza magnetica su di loro nella direzione opposta. L’equilibrio è raggiunto quando:
\
dove e è la grandezza della carica dell’elettrone, \(v_d\) è la velocità di deriva degli elettroni, ed E è la grandezza del campo elettrico creato dalla carica separata. Risolvendo questo per la velocità di deriva si ottiene
\
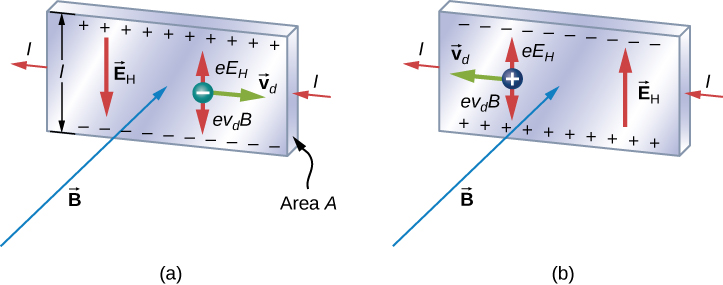
Uno scenario in cui i campi elettrico e magnetico sono perpendicolari tra loro è chiamato situazione di campo incrociato. Se questi campi producono forze uguali e opposte su una particella carica con la velocità che equipara le forze, queste particelle sono in grado di passare attraverso un apparato, chiamato selettore di velocità, senza essere deflesse. Questa velocità è rappresentata nell’equazione 11.26. Qualsiasi altra velocità di una particella carica inviata negli stessi campi verrebbe deflessa dalla forza magnetica o dalla forza elettrica.
Tornando all’effetto Hall, se la corrente nella striscia è I, allora da Corrente e Resistenza, sappiamo che
\
dove n è il numero di portatori di carica per volume e A è la sezione trasversale della striscia. Combinando le equazioni per \(v_d\) e I si ottiene
Il campo E è legato alla differenza di potenziale V tra i bordi della striscia da
La quantità \(V\) è chiamata potenziale di Hall e può essere misurata con un voltmetro. Infine, combinando le equazioni per I ed E si ottiene
dove il bordo superiore della striscia in figura \(\PageIndex{1}) è positivo rispetto al bordo inferiore.
Possiamo anche combinare l’equazione \ref{11.24} e l’equazione \ref{11.28} per ottenere un’espressione per la tensione di Hall in termini di campo magnetico:
E se i portatori di carica sono positivi, come nella figura \(\PageIndex{1}})? Per la stessa corrente I, la grandezza di V è ancora data dall’equazione \ref{hallV}. Tuttavia, il bordo superiore è ora negativo rispetto al bordo inferiore. Quindi, misurando semplicemente il segno di V, possiamo determinare il segno dei portatori di carica maggioritari in un metallo.
Le misure del potenziale di Hall mostrano che gli elettroni sono i portatori di carica dominanti nella maggior parte dei metalli. Tuttavia, i potenziali di Hall indicano che per alcuni metalli, come il tungsteno, il berillio e molti semiconduttori, la maggioranza dei portatori di carica è positiva. Si scopre che la conduzione per carica positiva è causata dalla migrazione di siti di elettroni mancanti (chiamati buchi) sugli ioni. La conduzione per buchi è studiata più avanti in Fisica della materia condensata.
L’effetto Hall può essere usato per misurare i campi magnetici. Se un materiale con una densità nota di portatori di carica n è posto in un campo magnetico e si misura V, allora il campo può essere determinato dall’equazione \ref{11.29}. Nei laboratori di ricerca dove i campi degli elettromagneti usati per misure precise devono essere estremamente stabili, una “sonda di Hall” è comunemente usata come parte di un circuito elettronico che regola il campo.
Esempio \(\PageIndex{1}): Selettore di velocità
Un fascio di elettroni entra in un selettore di velocità a campo incrociato con campi magnetici ed elettrici di 2,0 mT e \(6,0 \volte 10^3 \, N/C\), rispettivamente. (a) Quale deve essere la velocità del fascio di elettroni per attraversare i campi incrociati senza deflessione? Se il campo elettrico è spento, (b) qual è l’accelerazione del fascio di elettroni e (c) qual è il raggio del moto circolare che ne risulta?
Strategia
Il fascio di elettroni non viene deviato da nessuno dei campi magnetici o elettrici se queste forze sono bilanciate. Sulla base di queste forze bilanciate, calcoliamo la velocità del fascio. Senza il campo elettrico, solo la forza magnetica è usata nella seconda legge di Newton per trovare l’accelerazione. Infine, il raggio del percorso si basa sul moto circolare risultante dalla forza magnetica.
Soluzione
- La velocità del fascio imperturbato di elettroni con campi incrociati è calcolata dall’equazione \ref{11.25}: \L’accelerazione è calcolata dalla forza netta del campo magnetico, pari alla massa per l’accelerazione. La grandezza dell’accelerazione è: \ \
- Il raggio del percorso deriva da un equilibrio delle forze circolari e magnetiche, o dall’equazione \ref{11.25}: \
Significato
Se gli elettroni nel fascio avessero velocità superiori o inferiori alla risposta nella parte (a), questi elettroni avrebbero una forza netta più forte esercitata dal campo magnetico o elettrico. Pertanto, solo gli elettroni a questa specifica velocità riuscirebbero a passare.
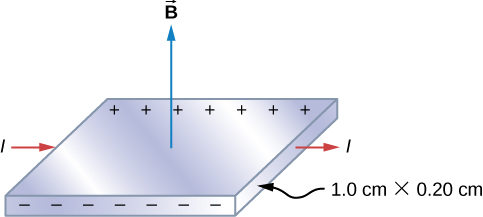
Il potenziale di Hall in un nastro d’argento
La figura (\PageIndex{2}) mostra un nastro d’argento la cui sezione è 1,0 cm per 0,20 cm. Il nastro porta una corrente di 100 A da sinistra a destra, e si trova in un campo magnetico uniforme di magnitudine 1,5 T. Usando un valore di densità di \(n = 5,9 \volte 10^{28}) elettroni per metro cubo per l’argento, trova il potenziale di Hall tra i bordi del nastro.
Strategia
Siccome la maggioranza dei portatori di carica sono elettroni, la polarità della tensione di Hall è quella indicata nella figura. Il valore della tensione di Hall si calcola con l’equazione \ref{hallV}.
Soluzione
Per calcolare la tensione di Hall, dobbiamo conoscere la corrente attraverso il materiale, il campo magnetico, la lunghezza, il numero di portatori di carica e l’area. Poiché tutti questi elementi sono dati, la tensione di Hall si calcola come:
&= \frac{(100 \, A)(1.5 \, T)(1,0 \volte 10^{-2}m)}(5,9 \volte 10^{28} /m^3)(1,6 \volte 10^{-19}C)(2,0 \volte 10^{-5}m^2)} &= 7,9 volte 10^{6}V. \end{align*}
Significato
Come in questo esempio, il potenziale di Hall è generalmente molto piccolo, e la sua misurazione richiede un’attenta sperimentazione con apparecchiature sensibili.
Esercizio \(\PageIndex{1})
Una sonda di Hall consiste in una striscia di rame, \(n = 8,5 \volte 10^{28}\) di elettroni per metro cubo, larga 2,0 cm e spessa 0,10 cm. Qual è il campo magnetico quando I = 50 A e il potenziale di Hall è
- (4.0 \, \mu V\) e
- (6.0 \, \mu V\)?
Risposta a
1.1 T
Risposta b
1.6 T
Contribuenti e attribuzioni
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs con molti autori che hanno contribuito. Questo lavoro è concesso in licenza da OpenStax University Physics sotto una licenza Creative Commons Attribution License (by 4.0).