Fondamenti di base della rappresentazione grafica Funzioni esponenziali
La funzione esponenziale y=b^x dove b>0 è una funzione che rimane proporzionale al suo valore originale quando cresce o decade.
Obiettivi di apprendimento
Descrivere le proprietà dei grafici delle funzioni esponenziali
Punti chiave
Punti chiave
- Se la base, b, è maggiore di 1, allora la funzione aumenta esponenzialmente con un tasso di crescita di b. Questo è noto come crescita esponenziale.
- Se la base, b, è minore di 1 (ma maggiore di 0) la funzione diminuisce esponenzialmente ad un tasso di b. Questo è noto come decadimento esponenziale.
- Se la base, b, è uguale a 1, allora la funzione diventa banalmente y=a.
- I punti (0,1) e (1,b) sono sempre sul grafico della funzione y=b^x
- La funzione y=b^x assume solo valori positivi e ha l’asse x come asintoto orizzontale.
Termini chiave
- crescita esponenziale: La crescita del valore di una quantità, in cui il tasso di crescita è proporzionale al valore istantaneo della quantità; per esempio, quando il valore è raddoppiato, anche il tasso di aumento sarà raddoppiato. Il tasso può essere positivo o negativo. Se negativo, è anche conosciuto come decadimento esponenziale.
- asintoto: Una linea a cui una curva si avvicina arbitrariamente. Un asintoto può essere verticale, obliquo o orizzontale. Gli asintoti orizzontali corrispondono al valore a cui la curva si avvicina quando x diventa molto grande o molto piccolo.
- funzione esponenziale: Qualsiasi funzione in cui una variabile indipendente è sotto forma di esponente; sono le funzioni inverse dei logaritmi.
Definizioni
Al livello più elementare, una funzione esponenziale è una funzione in cui la variabile appare nell’esponente. La funzione esponenziale più elementare è una funzione della forma y=b^x dove b è un numero positivo.
Quando b>1 la funzione cresce in modo proporzionale al suo valore originale. Questa è chiamata crescita esponenziale.
Quando 0>b>1 la funzione decade in modo proporzionale al suo valore originale. Questo è chiamato decadimento esponenziale.
Grafico di una funzione esponenziale
Consideriamo la funzione y=2^x quando b>1. Un modo di rappresentare questa funzione è quello di scegliere i valori di x e sostituirli nell’equazione per generare i valori di y. Così facendo possiamo ottenere i seguenti punti:
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) e (2,4)
Collegando i punti, si noterà una curva regolare che attraversa l’asse y nel punto (0,1) e che aumenta man mano che x assume valori sempre maggiori. Cioè, la curva si avvicina all’infinito quando x si avvicina all’infinito. Man mano che x assume valori sempre più piccoli, la curva si avvicina sempre più all’asse delle x. Cioè, la curva si avvicina a zero quando x si avvicina all’infinito negativo, rendendo l’asse x un asintoto orizzontale della funzione. Il punto (1,b) è sul grafico. Questo è vero per il grafico di tutte le funzioni esponenziali della forma y=b^x per x>1.
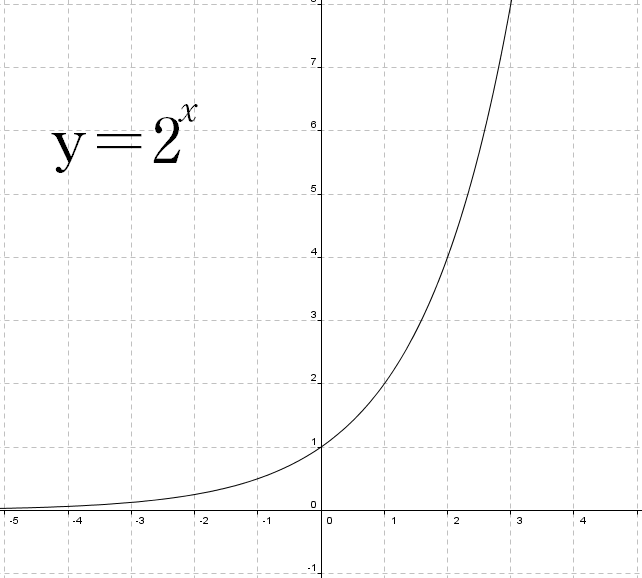
Grafico di y=2^x: Il grafico di questa funzione incrocia l’asse y in (0,1) e aumenta man mano che x si avvicina all’infinito. L’asse x è un asintoto orizzontale della funzione.
Esempio 2
Consideriamo la funzione y=frac{1}{2}^x quando 0<b<1. Un modo per tracciare il grafico di questa funzione è scegliere i valori di x e sostituirli nell’equazione per generare i valori di y. Così facendo si possono ottenere i seguenti punti:
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) e (2,\frac{1}{4})
Come si collegano i punti si noterà una curva regolare che attraversa l’asse y nel punto (0,1) ed è decrescente come x assume valori sempre più grandi. La curva si avvicina all’infinito zero man mano che si avvicina all’infinito. Man mano che x assume valori sempre più piccoli, la curva si avvicina sempre più all’asse x. Cioè, la curva si avvicina a zero quando x si avvicina all’infinito negativo, rendendo l’asse x un asintoto orizzontale della funzione. Il punto (1,b) è sul grafico. Questo è vero per il grafico di tutte le funzioni esponenziali della forma y=b^x per 0<x<1.
Come si può vedere nel grafico qui sotto, il grafico di y=frac{1}{2}^x è simmetrico a quello di y=2^x sull’asse y. Cioè, se il piano fosse piegato sull’asse y, le due curve giacerebbero l’una sull’altra.
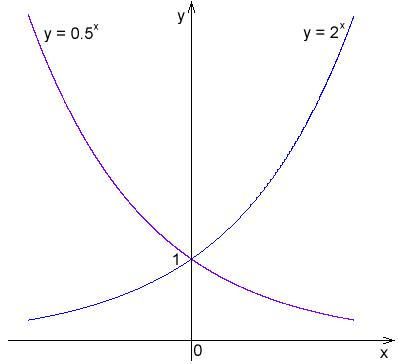
Grafico di y=2^x e y=frac{1}{2}^x: I grafici di queste funzioni sono simmetrici sull’asse y.
Perché b deve essere un numero positivo?
Se b=1, allora la funzione diventa y=1^x. Poiché 1 a qualsiasi potenza produce 1, la funzione è equivalente a y=1 che è una linea orizzontale, non un’equazione esponenziale.
Se b è negativo, allora elevando b a una potenza pari si ottiene un valore positivo per y mentre elevando b a una potenza dispari si ottiene un valore negativo per y, rendendo impossibile unire i punti ottenuti in qualsiasi modo significativo e certamente non in un modo che generi una curva come quelle negli esempi precedenti.
Proprietà dei grafici esponenziali
Il punto (0,1) è sempre sul grafico di una funzione esponenziale della forma y=b^x perché b è positivo e qualsiasi numero positivo alla potenza zero produce 1.
Il punto (1,b) è sempre sul grafico di una funzione esponenziale della forma y=b^x perché qualsiasi numero positivo b elevato alla prima potenza produce 1.
La funzione y=b^x assume solo valori positivi perché qualsiasi numero positivo b produce solo valori positivi se elevato a qualsiasi potenza.
La funzione y=b^x ha l’asse x come asintoto orizzontale perché la curva si avvicinerà sempre all’asse x quando x si avvicina all’infinito positivo o negativo, ma non attraverserà mai l’asse perché non sarà mai uguale a zero.
Grafici di funzioni logaritmiche
Le funzioni logaritmiche possono essere graficate manualmente o elettronicamente con punti generalmente determinati tramite una calcolatrice o una tabella.
Obiettivi di apprendimento
Descrivere le proprietà dei grafici delle funzioni logaritmiche
Punti chiave
Punti chiave
- Quando è rappresentata in forma grafica, la funzione logaritmica è simile alla funzione radice quadrata, ma con un asintoto verticale quando x si avvicina a 0 da destra.
- Il punto (1,0) è sul grafico di tutte le funzioni logaritmiche della forma y=log{_b}x, dove b è un numero reale positivo.
- Il dominio della funzione logaritmica y=log{_b}x, dove b è tutti i numeri reali positivi, è l’insieme di tutti i numeri reali positivi, mentre l’intervallo di questa funzione è tutti i numeri reali.
- Il grafico di una funzione logaritmica della forma y=log{_b}x può essere spostato in orizzontale e/o in verticale aggiungendo una costante alla variabile x o a y, rispettivamente.
- Una funzione logaritmica della forma y=log{_b}x dove b è un numero reale positivo, può essere rappresentata graficamente usando una calcolatrice per determinare i punti sul grafico o può essere rappresentata senza una calcolatrice usando il fatto che il suo inverso è una funzione esponenziale.
Termini chiave
- funzione logaritmica: Qualsiasi funzione in cui una variabile indipendente appare sotto forma di logaritmo. L’inverso di una funzione logaritmica è una funzione esponenziale e viceversa.
- logaritmo: Il logaritmo di un numero è l’esponente di cui un altro valore fisso, la base, deve essere aumentato per produrre quel numero.
- asintoto: Una linea a cui una curva si avvicina arbitrariamente. Gli asintoti possono essere orizzontali, verticali o obliqui.
Di seguito i grafici delle funzioni logaritmiche con basi 2, e, e 10.
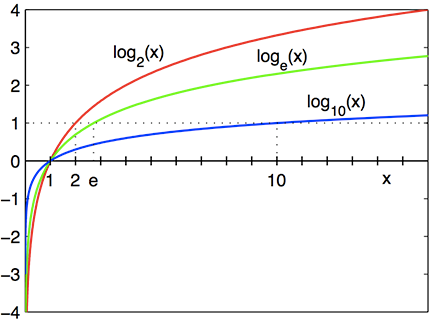
Grafici logaritmici: Dopo x=1, dove i grafici incrociano l’asse x, \log_2(x) in rosso è sopra \log_e(x) in verde, che è sopra \log_{10}(x) in blu. Prima di questo punto, l’ordine è invertito. Tutti e tre i logaritmi hanno l’asse y come asintoto verticale, e sono sempre crescenti.
Tutti e tre i grafici logaritmici iniziano con una ripida salita dopo x=0, ma si estendono sempre più orizzontalmente, la loro pendenza diminuisce sempre di più all’aumentare di x. Tutti loro incrociano l’asse x in x=1.
Proprietà dei grafici delle funzioni logaritmiche
Il grafico incrocia l’asse x in 1. Cioè, il grafico ha un’intercetta x di 1, e come tale, il punto (1,0) è sul grafico. Infatti, il punto (1,0) sarà sempre sul grafico di una funzione della forma y=log{_b}x dove b>0. Questo perché per x=1, l’equazione del grafico diventa y=log{_b}1.
Quindi, stiamo cercando un esponente y tale che b^y=1. Poiché b>0, l’esponente che cerchiamo è 1 indipendentemente dal valore di b. Questo significa che il punto (x,y)=(1,0) sarà sempre su una funzione logaritmica di questo tipo.
Asintoti
L’asse y è un asintoto verticale del grafico. Questo significa che la curva si avvicina sempre più all’asse y ma non lo attraversa.
Consideriamo cosa succede quando il valore di x si avvicina a zero da destra per l’equazione il cui grafico appare sopra. Vale a dire, y=log{_b}x. Possiamo farlo scegliendo i valori di x, inserendoli nell’equazione e generando i valori di y.
Assumiamo che b sia un numero positivo maggiore di 1, e studiamo i valori di x tra 0 e 1. In queste condizioni, se lasciamo che x=frac{1}{b}, l’equazione diventa y=logfrac{1}{b}.
Quindi, stiamo cercando un esponente tale che b elevato a quell’esponente produca \frac{1}{b}. L’esponente che cerchiamo è -1 e il punto (\frac{1}{b},-1) è sul grafico. Allo stesso modo, possiamo ottenere i seguenti punti che sono anch’essi sul grafico:
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) e così via
Se prendiamo valori di x che sono ancora più vicini a 0, possiamo arrivare ai seguenti punti: (\frac{1}{b^{10}},-10),(\frac{1}{b^{100}},-100) e (\frac{1}{b^{1000}},-1000)
Come si può vedere più il valore di x si avvicina a 0, più il grafico diventa negativo. Cioè, man mano che x si avvicina allo zero il grafico si avvicina all’infinito negativo. Questo significa che l’asse y è un asintoto verticale della funzione.
Dominio e intervallo
Il dominio della funzione sono tutti i numeri positivi. Ciò significa che il valore x della funzione sarà sempre positivo. Cominciamo a considerare perché il valore di x della curva non è mai 0.
Se il valore di x fosse zero, la funzione sarebbe y=log{_b}0.
Qui stiamo cercando un esponente tale che b elevato a tale esponente sia 0. Poiché b è un numero positivo, non c’è nessun esponente a cui possiamo elevare b in modo da ottenere 0. Infatti, poiché b è positivo, elevandolo a una potenza si ottiene sempre un numero positivo.
L’intervallo della funzione è costituito da tutti i numeri reali. Cioè, il grafico può assumere qualsiasi numero reale.
Confronto tra y=log{_x} e y=sqrt{x}
A prima vista, il grafico della funzione logaritmica può essere facilmente confuso con quello della funzione radice quadrata.
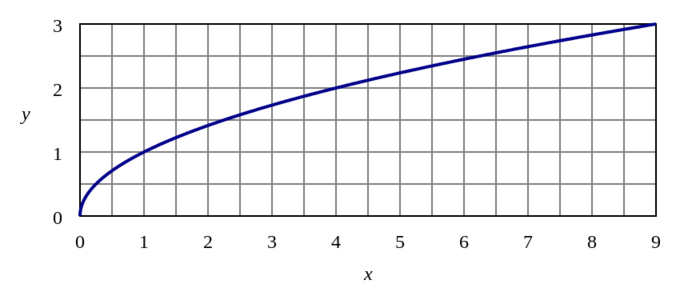
Grafico di y = sqrt{x}: Il grafico della funzione radice quadrata assomiglia al grafico della funzione logaritmica, ma non ha un asintoto verticale.
Entrambe le funzioni radice quadrata e logaritmica hanno un dominio limitato ai valori di x maggiori di 0. Tuttavia, la funzione logaritmica ha un asintoto verticale che scende verso -\infty quando x si avvicina a 0, mentre la radice quadrata raggiunge un valore y minimo di 0. L’intervallo della funzione radice quadrata è costituito da tutti i numeri reali non negativi, mentre l’intervallo della funzione logaritmica è costituito da tutti i numeri reali.
Grafico delle funzioni logaritmiche
La rappresentazione grafica delle funzioni logaritmiche può essere fatta individuando i punti sulla curva sia manualmente che con una calcolatrice.
Quando si fa il grafico senza calcolatrice, si usa il fatto che l’inverso di una funzione logaritmica è una funzione esponenziale.
Quando facciamo il grafico con la calcolatrice, usiamo il fatto che la calcolatrice può calcolare solo logaritmi comuni (la base è 10), logaritmi naturali (la base è e) o logaritmi binari (la base è 2). Naturalmente, se abbiamo una calcolatrice grafica, la calcolatrice può tracciare il grafico della funzione senza la necessità di trovare punti sul grafico.
Grafico di funzioni logaritmiche usando i loro inversi
Le funzioni logaritmiche possono essere tracciate a mano senza l’uso di una calcolatrice se usiamo il fatto che sono inversi delle funzioni esponenziali.
Consideriamo ancora il grafico della seguente funzione:
y=log{_3}x
Questa può essere scritta in forma esponenziale come:
3^y=x
Ora consideriamo l’inverso di questa funzione. Per farlo, scambiamo x e y:
3^x=y
La funzione esponenziale 3^x=y è una di quelle per cui possiamo facilmente generare punti. Se prendiamo alcuni valori di x e li inseriamo nell’equazione per trovare i corrispondenti valori di y possiamo ottenere i seguenti punti:
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) e (3,27)
Ora dobbiamo notare che questi punti non sono sulla funzione originale (y=log{_3}x) ma piuttosto sul suo inverso 3^x=y. Tuttavia, se scambiamo le coordinate x e y di ogni punto, otterremo in effetti una lista di punti sulla funzione originale.
Questi sono: (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) e (27,3).
Tracciamo e colleghiamo questi punti per ottenere il grafico della funzione y=log{3}x qui sotto.

Grafico di y=log{_3}x: Il grafico della funzione logaritmica con base 3 può essere generato utilizzando l’inverso della funzione. La sua forma è la stessa delle altre funzioni logaritmiche, solo con una scala diversa.
Grafico delle funzioni logaritmiche con basi tra 0 e 1
Finora abbiamo graficato le funzioni logaritmiche le cui basi sono maggiori di 1. Se invece consideriamo le funzioni logaritmiche con base b, tale che 0<b<1, otteniamo un grafico molto simile a quelli che abbiamo già visto.
Infatti se b>0, il grafico di y=log{b}x e il grafico di y=log{_frac{1}{b}x sono simmetrici sull’asse x. Quindi, se identifichiamo un punto (x,y) sul grafico di y=log{_b}x, possiamo trovare il punto corrispondente su y=log{_frac{1}{b}x cambiando il segno dell’ordinata. Il punto corrispondente è (x,-y).
Ecco un esempio per b=2.
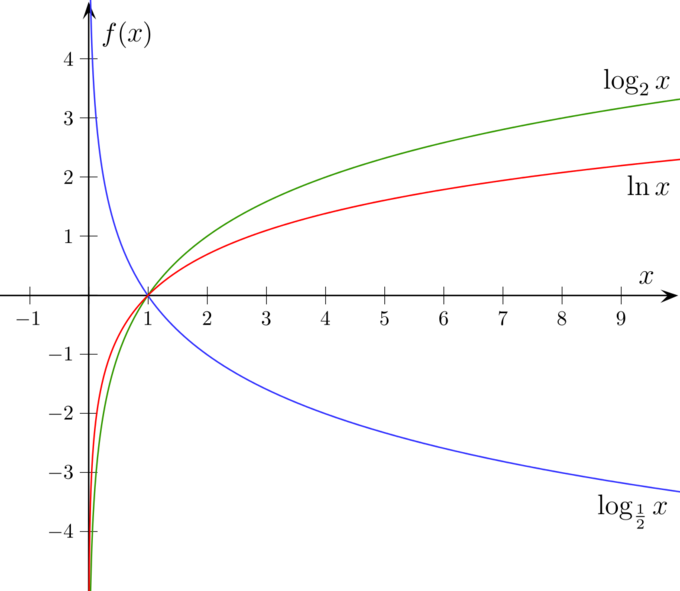
Grafici di log{_2}x e log{_\frac{1}{2}}x : I grafici di log_2 x e log{_\frac{2}{2}x sono simmetrici sull’asse delle x
Risolvere i problemi con i grafici logaritmici
Alcune funzioni di forma rapidamente variabile sono meglio tracciate su una scala che aumenta esponenzialmente, come un grafico logaritmico.
Obiettivi di apprendimento
Convertire i problemi in scale logaritmiche e discuterne i vantaggi
Punti chiave
Punti chiave
- I grafici logaritmici usano scale logaritmiche, in cui i valori differiscono esponenzialmente. Per esempio, invece di includere segni a 0,1,2 e 3, una scala logaritmica può includere segni a 0,1, 1, 10 e 100, ognuno a uguale distanza dal precedente e dal successivo.
- I grafici logaritmici permettono di tracciare una gamma molto ampia di dati senza perdere la forma del grafico.
- I grafici logaritmici rendono più facile interpolare in aree che possono essere difficili da leggere su assi lineari. Per esempio, se il grafico y=x^5 è scalato per mostrare una gamma molto ampia di valori y, la curvatura vicino all’origine può essere indistinguibile sugli assi lineari. È molto più chiaro sugli assi logaritmici.
Termini chiave
- logaritmo: Il logaritmo di un numero è l’esponente di cui un altro valore fisso, la base, deve essere aumentato per produrre quel numero.
- interpolare: Per stimare il valore di una funzione tra due punti tra i quali è tabulato.
Perché usare una scala logaritmica?
Molte relazioni matematiche e fisiche sono funzionalmente dipendenti da variabili di ordine superiore. Questo significa che per piccoli cambiamenti nella variabile indipendente ci sono cambiamenti molto grandi nella variabile dipendente. Quindi, diventa difficile graficare tali funzioni sull’asse standard.
Consideriamo, come esempio, la legge di Stefan-Boltzmann, che mette in relazione la potenza (j*) emessa da un corpo nero con la temperatura (T).
j^*= \sigma T^4
Su un grafico standard, questa equazione può essere abbastanza ingombrante. La dipendenza di quarto grado dalla temperatura significa che la potenza aumenta estremamente rapidamente. Il fatto che il tasso sia sempre crescente (e in modo ripido) significa che cambiare scala (scalare gli assi di 5, 10 o anche 100) è di scarso aiuto nel rendere il grafico più facile da interpretare.
Per funzioni molto ripide, è possibile tracciare i punti in modo più uniforme mantenendo l’integrità dei dati: si può usare un grafico con una scala logaritmica, dove invece di rappresentare un aumento costante, ogni spazio su un grafico rappresenta un aumento esponenziale. Dove un grafico normale (lineare) potrebbe avere intervalli uguali che vanno 1, 2, 3, 4, una scala logaritmica avrebbe quegli stessi intervalli uguali che rappresentano 1, 10, 100, 1000. Ecco alcuni esempi di funzioni graficate su una scala lineare, semi-logica e logaritmica.
L’alto a sinistra è una scala lineare. Quella in basso a destra è una scala logaritmica. L’alto a destra e il basso a sinistra sono chiamate scale semi-logiche perché un asse è scalato linearmente mentre l’altro è scalato usando i logaritmi.

Scala logaritmica: I grafici delle funzioni f(x)=10^x,f(x)=x e f(x)=log x su quattro diversi grafici di coordinate. In alto a sinistra è una scala lineare, in alto a destra e in basso a sinistra sono scale semi-log e in basso a destra è una scala logaritmica.
Come potete vedere, quando entrambi gli assi hanno usato una scala logaritmica (in basso a destra) il grafico ha mantenuto le proprietà del grafico originale (in alto a sinistra) dove entrambi gli assi sono stati scalati usando una scala lineare. Questo significa che se vogliamo rappresentare una funzione che è ingombrante su una scala lineare possiamo usare una scala logaritmica su ogni asse e mantenere le proprietà del grafico e allo stesso tempo renderlo più facile da rappresentare.
Con le scale semi-logiche, le funzioni hanno forme che sono oblique rispetto all’originale. Quando solo l’asse x ha una scala logaritmica, la curva logaritmica appare come una linea e le curve lineari ed esponenziali sembrano entrambe esponenziali. Quando solo l’asse y ha una scala logaritmica, la curva esponenziale appare come una linea e le curve lineari e logaritmiche appaiono entrambe logaritmiche.Va notato che gli esempi nei grafici avevano lo scopo di illustrare un punto e che le funzioni graficate non erano necessariamente ingombranti su una serie di assi a scala lineare.
Convertire le scale lineari in logaritmiche
La differenza principale tra le scale logaritmiche e quelle lineari è che, mentre la differenza di valore tra punti lineari di uguale distanza rimane costante (cioè, se lo spazio da 0 a 1 sulla scala è 1 cm sulla pagina, la distanza da 1 a 2, 2 a 3, ecc, sarà la stessa), la differenza di valore tra punti su una scala logaritmica cambierà esponenzialmente. Una scala logaritmica inizierà ad una certa potenza di 10, e con ogni unità aumenterà di una potenza di 10.
Quindi, se si volesse convertire una scala lineare (con valori 0-5 in una scala logaritmica, una possibilità sarebbe quella di sostituire 1,2,3,4 e 5 con 0.001,0.01,0.1,1,10 e 100, rispettivamente. Tra ogni valore maggiore sulla scala logaritmica, gli hashmarks diventano sempre più vicini con l’aumentare del valore. Per esempio, nello spazio tra 1 e 10, l’8 e il 9 sono molto più vicini del 2 e del 3.
I vantaggi di usare una scala logaritmica sono due. In primo luogo, questo permette di tracciare una gamma molto ampia di dati senza perdere la forma del grafico. In secondo luogo, permette di interpolare in qualsiasi punto del grafico, indipendentemente dall’intervallo del grafico. Dati simili tracciati su una scala lineare sono meno chiari.
Risolvere i problemi usando i grafici logaritmici
Un punto chiave sull’uso dei grafici logaritmici per risolvere i problemi è che essi espandono le scale fino al punto in cui grandi intervalli di dati hanno più senso. Nell’equazione di cui sopra (j^*= \sigma T^4), tracciare j contro T genererebbe la curva prevista, ma la scala sarebbe tale che i cambiamenti minimi passano inosservati e gli effetti su larga scala della relazione dominano il grafico: È così grande che le “aree interessanti” non si adatterebbero alla carta in una scala leggibile.
Prendendo il logaritmo di ogni lato delle equazioni si ottiene: logj=log{(\sigma\tau ) }^4 . Ora ci affidiamo alle proprietà dei logaritmi per riscrivere l’equazione.
Ricordiamo le seguenti proprietà dei logaritmi:
\log(ab)=\log(a)+\log(b) \log(a)^b=(b)\log(a)
Utilizzando quanto sopra, la nostra equazione diventa:
begin{align} \log j&=4\log{(\sigma\tau ) } &=4\log{(\sigma)}+4\log{(\tau ) } \Design&=4\log{(\tau )}+4\log{(\sigma)} \end{align}