Una base vettoriale di uno spazio vettoriale 
è definita come un sottoinsieme 
di vettori in 
che sono linearmente indipendenti e spaziano 
. Di conseguenza, se 
è una lista di vettori in 
, allora questi vettori formano una base vettoriale se e solo se ogni 
può essere scritto univocamente come
 |
(1)
|
dove 
sono elementi del campo base.
Quando il campo base sono i reali in modo che 
per 
, i vettori base risultanti sono 
-tuple di reali che spaziano 
spazio euclideo dimensionale 
. Altri possibili campi base includono i complessi 
, così come vari campi di caratteristica positiva considerati in algebra, teoria dei numeri e geometria algebrica.
Uno spazio vettoriale 
ha molte basi vettoriali diverse, ma ci sono sempre lo stesso numero di vettori base in ciascuna di esse. Il numero di vettori base in 
si chiama dimensione di 
. Ogni lista spaziale in uno spazio vettoriale può essere ridotta a una base dello spazio vettoriale.
L’esempio più semplice di una base vettoriale è la base standard nello spazio euclideo 
, in cui i vettori base giacciono lungo ogni asse delle coordinate. Un cambio di base può essere usato per trasformare i vettori (e gli operatori) in una data base in un’altra.
Dato un iperpiano definito da
 |
(2)
|
una base può essere trovata risolvendo 
in termini di 
, e 
. Eseguendo questa procedura,
 |
(3)
|
così
 |
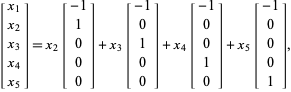(4)
|
e i vettori precedenti formano una base (non normalizzata).
Data una matrice 
con una base ortonormale, la matrice corrispondente a un cambiamento di base, espressa in termini dell’originale 
è
 |
(5)
|
Quando uno spazio vettoriale è infinitamente dimensionale, allora esiste una base finché si assume l’assioma della scelta. Un sottoinsieme della base che è linearmente indipendente e il cui span è denso è chiamato un insieme completo, ed è simile a una base. Quando 
è uno spazio di Hilbert, un insieme completo si chiama base di Hilbert.