Básicos de la gráfica. Funciones exponenciales
La función exponencial y=b^x donde b>0 es una función que permanecerá proporcional a su valor original cuando crezca o decaiga.
Objetivos de aprendizaje
Describir las propiedades de las gráficas de las funciones exponenciales
Puntos clave
Puntos clave
- Si la base, b, es mayor que 1, entonces la función aumenta exponencialmente a una tasa de crecimiento de b. Esto se conoce como crecimiento exponencial.
- Si la base, b, es menor que 1 (pero mayor que 0) la función disminuye exponencialmente a una tasa de b. Esto se conoce como decaimiento exponencial.
- Si la base, b, es igual a 1, entonces la función se convierte trivialmente en y=a.
- Los puntos (0,1) y (1,b) están siempre en la gráfica de la función y=b^x
- La función y=b^x sólo toma valores positivos y tiene el eje x como asíntota horizontal.
Términos clave
- Crecimiento exponencial: El crecimiento del valor de una cantidad, en el que la tasa de crecimiento es proporcional al valor instantáneo de la cantidad; por ejemplo, cuando el valor se ha duplicado, la tasa de aumento también se habrá duplicado. La tasa puede ser positiva o negativa. Si es negativa, también se conoce como decaimiento exponencial.
- Asíntota: Línea a la que una curva se aproxima arbitrariamente. Una asíntota puede ser vertical, oblicua u horizontal. Las asíntotas horizontales corresponden al valor al que se aproxima la curva cuando x se hace muy grande o muy pequeña.
- Función exponencial: Cualquier función en la que una variable independiente está en forma de exponente; son las funciones inversas de los logaritmos.
Definiciones
En el nivel más básico, una función exponencial es una función en la que la variable aparece en el exponente. La función exponencial más básica es una función de la forma y=b^x donde b es un número positivo.
Cuando b>1 la función crece de forma proporcional a su valor original. Esto se llama crecimiento exponencial.
Cuando 0>b>1 la función decae de forma proporcional a su valor original. Esto se llama decaimiento exponencial.
Graficación de una función exponencial
Consideremos la función y=2^x cuando b>1. Una forma de graficar esta función es elegir valores para x y sustituirlos en la ecuación para generar valores para y. Haciendo esto podemos obtener los siguientes puntos:
(-2,\frac{1}{4}), (-1,\frac{1}{2}), (0,1), (1,2) y (2,4)
Al conectar los puntos, notaremos una curva suave que cruza el eje y en el punto (0,1) y es creciente a medida que x toma valores cada vez mayores. Es decir, la curva se acerca al infinito a medida que x se acerca al infinito. A medida que x toma valores cada vez más pequeños, la curva se acerca cada vez más al eje x. Es decir, la curva se aproxima a cero a medida que x se acerca al infinito negativo haciendo que el eje x sea una asíntota horizontal de la función. El punto (1,b) está en la gráfica. Esto ocurre con la gráfica de todas las funciones exponenciales de la forma y=b^x para x>1.

Gráfica de y=2^x: La gráfica de esta función cruza el eje y en (0,1) y aumenta a medida que x se acerca al infinito. El eje x es una asíntota horizontal de la función.
Ejemplo 2
Consideremos la función y=\frac{1}{2}^x cuando 0<b<1. Una forma de graficar esta función es elegir valores para x y sustituirlos en la ecuación para generar valores para y. Haciendo esto se pueden obtener los siguientes puntos:
(-2,4), (-1,2), (0,1), (1,\frac{1}{2}) y (2,\frac{1}{4})
Al conectar los puntos se observa una curva suave que cruza el eje y en el punto (0,1) y que es decreciente a medida que x toma valores cada vez mayores. La curva se aproxima al cero del infinito a medida que se aproxima al infinito. A medida que x toma valores cada vez más pequeños, la curva se acerca cada vez más al eje x. Es decir, la curva se aproxima a cero a medida que x se acerca a infinito negativo haciendo que el eje x sea una asíntota horizontal de la función. El punto (1,b) está en la gráfica. Esto se cumple en la gráfica de todas las funciones exponenciales de la forma y=b^x para 0<x<1.
Como puedes ver en la gráfica de abajo, la gráfica de y=frac{1}{2}^x es simétrica a la de y=2^x sobre el eje y. Es decir, si se doblara el plano sobre el eje y, las dos curvas quedarían una sobre la otra.
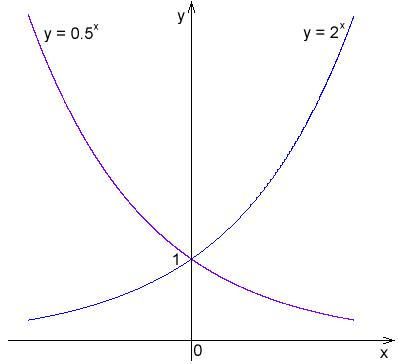
Gráfica de y=2^x e y=\frac{1}{2}^x: Las gráficas de estas funciones son simétricas sobre el eje y.
¿Por qué b debe ser un número positivo?
Si b=1, entonces la función se convierte en y=1^x. Como 1 a cualquier potencia da como resultado 1, la función es equivalente a y=1 que es una recta horizontal, no una ecuación exponencial.
Si b es negativo, entonces elevar b a una potencia par da como resultado un valor positivo para y mientras que elevar b a una potencia impar da como resultado un valor negativo para y, lo que hace imposible unir los puntos obtenidos de una forma significativa y desde luego no de una forma que genere una curva como las de los ejemplos anteriores.
Propiedades de las gráficas exponenciales
El punto (0,1) está siempre en la gráfica de una función exponencial de la forma y=b^x porque b es positivo y cualquier número positivo a la potencia cero da 1.
El punto (1,b) siempre está en la gráfica de una función exponencial de la forma y=b^x porque cualquier número positivo b elevado a la primera potencia da 1.
La función y=b^x sólo toma valores positivos porque cualquier número positivo b sólo dará valores positivos cuando se eleve a cualquier potencia.
La función y=b^x tiene el eje x como asíntota horizontal porque la curva siempre se acercará al eje x cuando x se acerque al infinito positivo o negativo, pero nunca cruzará el eje ya que nunca será igual a cero.
Gráficos de funciones logarítmicas
Las funciones logarítmicas se pueden graficar manualmente o electrónicamente con puntos generalmente determinados a través de una calculadora o tabla.
Objetivos de aprendizaje
Describir las propiedades de las gráficas de las funciones logarítmicas
Puntos clave
Puntos clave
- Cuando se representa gráficamente, la función logarítmica tiene una forma similar a la función de raíz cuadrada, pero con una asíntota vertical a medida que x se acerca a 0 desde la derecha.
- El punto (1,0) está en la gráfica de todas las funciones logarítmicas de la forma y=log{_b}x, donde b es un número real positivo.
- El dominio de la función logarítmica y=log{_b}x, donde b son todos los números reales positivos, es el conjunto de todos los números reales positivos, mientras que el rango de esta función son todos los números reales.
- La gráfica de una función logarítmica de la forma y=log{_b}x se puede desplazar horizontal y/o verticalmente añadiendo una constante a la variable x o a y, respectivamente.
- Una función logarítmica de la forma y=log{_b}x donde b es un número real positivo, puede graficarse utilizando una calculadora para determinar los puntos de la gráfica o puede graficarse sin calculadora utilizando el hecho de que su inversa es una función exponencial.
Términos clave
- Función logarítmica: Cualquier función en la que una variable independiente aparece en forma de logaritmo. La inversa de una función logarítmica es una función exponencial y viceversa.
- Logaritmo: El logaritmo de un número es el exponente por el que hay que elevar otro valor fijo, la base, para producir ese número.
- Asíntota: Línea a la que una curva se aproxima arbitrariamente. Las asíntotas pueden ser horizontales, verticales u oblicuas.
A continuación se muestran las gráficas de las funciones logarítmicas con bases 2, e y 10.

Gráficas logarítmicas: Después de x=1, donde las gráficas cruzan el eje x, \log_2(x) en rojo está por encima de \log_e(x) en verde, que está por encima de \log_{10}(x) en azul. Antes de este punto, el orden se invierte. Los tres logaritmos tienen el eje y como asíntota vertical, y son siempre crecientes.
Las tres gráficas logarítmicas comienzan con una subida pronunciada después de x=0, pero se estiran cada vez más horizontalmente, su pendiente siempre disminuye a medida que x aumenta. Todas ellas cruzan el eje x en x=1.
Propiedades de las gráficas de funciones logarítmicas
La gráfica cruza el eje x en 1. Es decir, la gráfica tiene una intersección x de 1, y como tal, el punto (1,0) está en la gráfica. De hecho, el punto (1,0) siempre estará en la gráfica de una función de la forma y=log{_b}x donde b>0. Esto se debe a que para x=1, la ecuación de la gráfica se convierte en y=log{_b}1.
Así, buscamos un exponente y tal que b^y=1. Como b>0, el exponente que buscamos es 1 independientemente del valor de b. Esto significa que el punto (x,y)=(1,0) siempre estará en una función logarítmica de este tipo.
Asíntotas
El eje y es una asíntota vertical de la gráfica. Esto significa que la curva se acerca cada vez más al eje y pero no lo cruza.
Consideremos lo que ocurre a medida que el valor de x se acerca a cero por la derecha para la ecuación cuya gráfica aparece arriba. A saber, y=log{_b}x. Podemos hacerlo eligiendo valores para x, enchufándolos en la ecuación y generando valores para y.
Supongamos que b es un número positivo mayor que 1, e investiguemos valores de x entre 0 y 1. En estas condiciones, si dejamos que x=\frac{1}{b}, la ecuación se convierte en y=log\frac{1}{b}.
Así, buscamos un exponente tal que b elevado a ese exponente dé como resultado \frac{1}{b}. El exponente que buscamos es -1 y el punto (\frac{1}{b},-1) está en la gráfica. De forma similar, podemos obtener los siguientes puntos que también están en la gráfica:
(\frac{1}{b^2},-2),(\frac{1}{b^3},-3),(\frac{1}{b^4},-4) y así sucesivamente
Si tomamos valores de x aún más cercanos a 0, podemos llegar a los siguientes puntos: (\frac{1}{b^{10}},-10),(\frac{1}{b^{100}},-100) y (\frac{1}{b^{1000}},-1000)
Como se puede observar cuanto más se acerca el valor de x a 0, más y más negativa se vuelve la gráfica. Es decir, a medida que x se acerca a cero la gráfica se aproxima al infinito negativo. Esto significa que el eje y es una asíntota vertical de la función.
Dominio y rango
El dominio de la función son todos los números positivos. Esto significa que el valor x de la función siempre será positivo. Empecemos por considerar por qué el valor x de la curva nunca es 0.
Si el valor x fuera cero, la función diría y=log{_b}0.
Aquí estamos buscando un exponente tal que b elevado a ese exponente sea 0. Como b es un número positivo, no hay ningún exponente al que podamos elevar b para obtener 0. De hecho, como b es positivo, elevarlo a una potencia siempre dará un número positivo.
El rango de la función son todos los números reales. Es decir, la gráfica puede tomar cualquier número real.
Comparando y=log{_x} e y=\sqrt{x}
A primera vista, la gráfica de la función logarítmica puede confundirse fácilmente con la de la función raíz cuadrada.
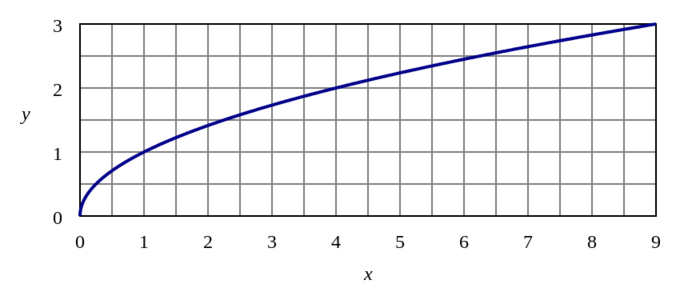
Gráfica de y=\sqrt{x}: La gráfica de la función raíz cuadrada se parece a la gráfica de la función logarítmica, pero no tiene asíntota vertical.
Tanto la función raíz cuadrada como la logarítmica tienen un dominio limitado a los valores de x mayores que 0. Sin embargo, la función logarítmica tiene una asíntota vertical que desciende hacia -\infty a medida que x se acerca a 0, mientras que la raíz cuadrada alcanza un valor y mínimo de 0. El rango de la función raíz cuadrada son todos los números reales no negativos, mientras que el rango de la función logarítmica son todos los números reales.
Graficación de funciones logarítmicas
La graficación de funciones logarítmicas se puede hacer localizando puntos en la curva de forma manual o con una calculadora.
Cuando se grafica sin calculadora, se utiliza el hecho de que la inversa de una función logarítmica es una función exponencial.
Cuando se hace la gráfica con calculadora, se utiliza el hecho de que la calculadora sólo puede calcular logaritmos comunes (la base es 10), logaritmos naturales (la base es e) o logaritmos binarios (la base es 2). Por supuesto, si tenemos una calculadora gráfica, la calculadora puede graficar la función sin necesidad de que encontremos puntos en la gráfica.
Graficación de funciones logarítmicas usando sus inversas
Las funciones logarítmicas se pueden graficar a mano sin necesidad de usar una calculadora si usamos el hecho de que son inversas de las funciones exponenciales.
Volvamos a considerar la gráfica de la siguiente función:
y=log{_3}x
Se puede escribir en forma exponencial como:
3^y=x
Ahora consideremos la inversa de esta función. Para ello, intercambiamos x e y:
3^x=y
La función exponencial 3^x=y es una para la que podemos generar puntos fácilmente. Si tomamos algunos valores de x y los enchufamos en la ecuación para encontrar los valores correspondientes de y podemos obtener los siguientes puntos:
(-2,\frac{1}{9}),(-1,\frac{1}{3}),(0,1),(1,3),(2,9) y (3,27)
Ahora debemos notar que estos puntos no están sobre la función original (y=log{3}x) sino sobre su inversa 3^x=y. Sin embargo, si intercambiamos las coordenadas x e y de cada punto obtendremos de hecho una lista de puntos sobre la función original.
Estos son: (\frac{1}{9},-2),(\frac{1}{3},-1),(1,0),(3,1),(9,2) y (27,3).
Ploteamos y conectamos estos puntos para obtener la gráfica de la función y=log{3}x que aparece a continuación.

Gráfica de y=log{3}x: La gráfica de la función logarítmica de base 3 se puede generar utilizando la inversa de la función. Su forma es la misma que la de otras funciones logarítmicas, sólo que con una escala diferente.
Gráfica de funciones logarítmicas con bases entre 0 y 1
Hasta ahora hemos graficado funciones logarítmicas cuyas bases son mayores que 1. Si en cambio consideramos funciones logarítmicas con base b, tal que 0<b<1, obtenemos una gráfica muy similar a las que ya hemos visto.
De hecho, si b>0, la gráfica de y=log{_b}x y la gráfica de y=log{_frac{1}{b}}x son simétricas sobre el eje x. Por lo tanto, si identificamos un punto (x,y) en la gráfica de y=log{b}x, podemos encontrar el punto correspondiente en y=log{_\frac{1}{b}x cambiando el signo de la coordenada y. El punto correspondiente es (x,-y).
Aquí tienes un ejemplo para b=2.
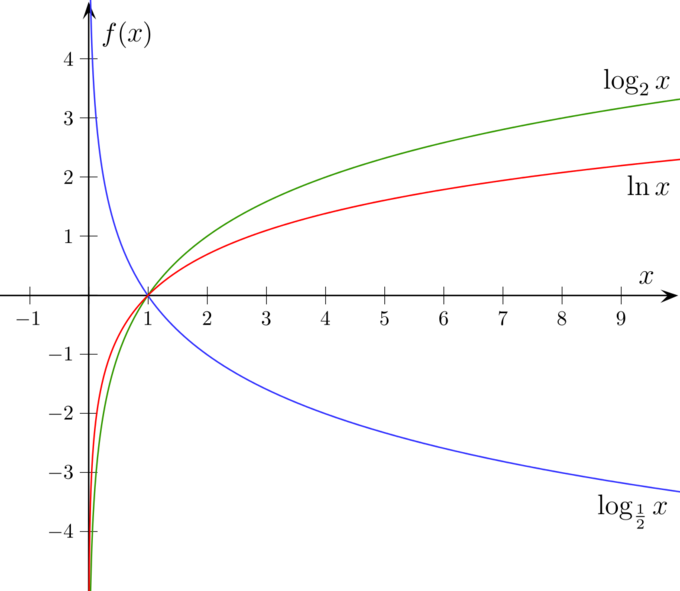
Gráficas de log{_2}x y log{_\frac{1}{2}}x : Las gráficas de log_2 x y log{\frac{1}{2}}x son simétricas sobre el eje x
Resolución de problemas con gráficas logarítmicas
Algunas funciones que cambian rápidamente de forma se representan mejor en una escala que aumenta exponencialmente, como una gráfica logarítmica.
Objetivos de aprendizaje
Convertir problemas a escalas logarítmicas y discutir las ventajas de hacerlo
Puntos clave
Puntos clave
- Las gráficas logarítmicas utilizan escalas logarítmicas, en las que los valores difieren exponencialmente. Por ejemplo, en lugar de incluir marcas en 0,1,2 y 3, una escala logarítmica puede incluir marcas en 0,1, 1, 10 y 100, cada una a igual distancia de la anterior y la siguiente.
- Los gráficos logarítmicos permiten trazar un rango muy grande de datos sin perder la forma del gráfico.
- Los gráficos logarítmicos facilitan la interpolación en áreas que pueden ser difíciles de leer en ejes lineales. Por ejemplo, si el gráfico y=x^5 se escala para mostrar un rango muy amplio de valores de y, la curvatura cerca del origen puede ser indistinguible en los ejes lineales. Es mucho más clara en los ejes logarítmicos.
Términos clave
- logaritmo: El logaritmo de un número es el exponente por el que hay que elevar otro valor fijo, la base, para producir ese número.
- interpolar: Estimar el valor de una función entre dos puntos entre los que está tabulada.
¿Por qué utilizar una escala logarítmica?
Muchas relaciones matemáticas y físicas dependen funcionalmente de variables de alto orden. Esto significa que para pequeños cambios en la variable independiente hay cambios muy grandes en la variable dependiente. Por lo tanto, se hace difícil graficar dichas funciones en el eje estándar.
Considere, como ejemplo, la ley de Stefan-Boltzmann, que relaciona la potencia (j*) emitida por un cuerpo negro con la temperatura (T).
j^*= \sigma T^4
En un gráfico estándar, esta ecuación puede ser bastante difícil de manejar. La dependencia de cuarto grado de la temperatura hace que la potencia aumente con extrema rapidez. El hecho de que la tasa sea cada vez mayor (y de forma pronunciada) significa que el cambio de escala (escalando los ejes por 5, 10 o incluso 100) es de poca ayuda para hacer que el gráfico sea más fácil de interpretar.
Para las funciones muy inclinadas, es posible trazar los puntos de forma más suave mientras se mantiene la integridad de los datos: se puede utilizar un gráfico con una escala logarítmica, donde en lugar de que cada espacio en un gráfico represente un aumento constante, representa un aumento exponencial. Mientras que un gráfico normal (lineal) podría tener intervalos iguales que fueran 1, 2, 3, 4, una escala logarítmica haría que esos mismos intervalos iguales representaran 1, 10, 100, 1000. Aquí hay algunos ejemplos de funciones graficadas en una escala lineal, semilogarítmica y logarítmica.
La parte superior izquierda es una escala lineal. La de abajo a la derecha es una escala logarítmica. La parte superior derecha y la inferior izquierda se denominan escalas semilogarítmicas porque un eje se escala linealmente mientras que el otro se escala utilizando logaritmos.

Escala logarítmica: Las gráficas de las funciones f(x)=10^x,f(x)=x y f(x)=\log x en cuatro gráficas de coordenadas diferentes. Arriba a la izquierda es una escala lineal, arriba a la derecha y abajo a la izquierda son escalas semilogarítmicas y abajo a la derecha es una escala logarítmica.
Como puedes ver, cuando ambos ejes utilizaron una escala logarítmica (abajo a la derecha) la gráfica conservó las propiedades de la gráfica original (arriba a la izquierda) donde ambos ejes fueron escalados utilizando una escala lineal. Esto significa que si queremos graficar una función que es difícil de manejar en una escala lineal, podemos usar una escala logarítmica en cada eje y conservar las propiedades del gráfico mientras que al mismo tiempo lo hace más fácil de graficar.
Con las escalas semilogarítmicas, las funciones tienen formas que están sesgadas en relación con el original. Cuando sólo el eje x tiene una escala logarítmica, la curva logarítmica aparece como una línea y las curvas lineal y exponencial parecen ambas exponenciales. Cuando sólo el eje y tiene una escala logarítmica, la curva exponencial aparece como una línea y las curvas lineal y logarítmica aparecen ambas como logarítmicas.Hay que tener en cuenta que los ejemplos de los gráficos pretendían ilustrar un punto y que las funciones graficadas no eran necesariamente difíciles de manejar en un conjunto de ejes de escala lineal.
Conversión de escalas lineales a logarítmicas
La principal diferencia entre las escalas logarítmicas y las lineales es que, mientras que la diferencia de valor entre puntos lineales de igual distancia permanece constante (es decir, si el espacio de 0 a 1 en la escala es de 1 cm en la página, la distancia de 1 a 2, 2 a 3, etc., será la misma), la diferencia de valor entre los puntos de una escala logarítmica cambiará exponencialmente. Una escala logarítmica comenzará en una determinada potencia de 10, y con cada unidad aumentará en una potencia de 10.
Así, si se quisiera convertir una escala lineal (con valores 0-5 a una escala logarítmica, una opción sería sustituir 1,2,3,4 y 5 por 0,001,0,01,0,1,10 y 100, respectivamente. Entre cada uno de los valores principales de la escala logarítmica, las marcas se acercan cada vez más al aumentar el valor. Por ejemplo, en el espacio entre el 1 y el 10, el 8 y el 9 están mucho más juntos que el 2 y el 3.
Las ventajas de utilizar una escala logarítmica son dobles. En primer lugar, permite trazar un rango muy grande de datos sin perder la forma del gráfico. En segundo lugar, permite interpolar en cualquier punto del gráfico, independientemente del rango del mismo. Datos similares trazados en una escala lineal son menos claros.
Resolución de problemas usando gráficas logarítmicas
Un punto clave sobre el uso de gráficas logarítmicas para resolver problemas es que expanden las escalas hasta el punto en que los grandes rangos de datos tienen más sentido. En la ecuación mencionada anteriormente (j^*= \sigma T^4), el trazado de j frente a T generaría la curva esperada, pero la escala sería tal que los cambios diminutos pasan desapercibidos y los efectos a gran escala de la relación dominan el gráfico: Es tan grande que las «zonas interesantes» no caben en el papel en una escala legible.
Tomando el logaritmo de cada lado de las ecuaciones se obtiene: logj=log{(\sigma\tau ) }^4 . Ahora nos basamos en las propiedades de los logaritmos para reescribir la ecuación.
Recordemos las siguientes propiedades de los logaritmos:
log(ab)=\log(a)+\log(b) \log(a)^b=(b)\log(a)
Usando lo anterior, nuestra ecuación se convierte en:
begin{align} \log j&=4\log{(\sigma\tau ) } &=4\log{(\sigma)}+4\log{(\tau ) } &=4\log{(\tau ) }+4\log{(\sigma)} igma)}end{align}