Objetivos de aprendizaje
Al finalizar esta sección, serás capaz de:
- Explicar un escenario en el que los campos magnético y eléctrico se cruzan y sus fuerzas se equilibran mientras una partícula cargada se mueve a través de un selector de velocidad
- Comparar cómo se mueven los portadores de carga en un material conductor y explicar cómo se relaciona esto con el efecto Hall
En 1879, E.H. Hall ideó un experimento que puede utilizarse para identificar el signo de los portadores de carga predominantes en un material conductor. Desde una perspectiva histórica, este experimento fue el primero en demostrar que los portadores de carga en la mayoría de los metales son negativos.
Visite este sitio web para encontrar más información sobre el efecto Hall.
Investigamos el efecto Hall estudiando el movimiento de los electrones libres a lo largo de una banda metálica de anchura l en un campo magnético constante (Figura \PageIndex{1}\}). Los electrones se mueven de izquierda a derecha, por lo que la fuerza magnética que experimentan los empuja hacia el borde inferior de la tira. Esto deja un exceso de carga positiva en el borde superior de la tira, dando lugar a un campo eléctrico E dirigido de arriba a abajo. La concentración de carga en ambos bordes aumenta hasta que la fuerza eléctrica sobre los electrones en una dirección se equilibra con la fuerza magnética sobre ellos en la dirección opuesta. El equilibrio se alcanza cuando:
donde e es la magnitud de la carga de los electrones, \(v_d\) es la velocidad de deriva de los electrones, y E es la magnitud del campo eléctrico creado por la carga separada. Resolviendo esto para la velocidad de deriva se obtiene
\Nque la carga de los electrones está separada de la carga, y E es la magnitud del campo eléctrico creado por la carga separada. En la figura a, una carga negativa se desplaza hacia la derecha con una velocidad v d. Las cargas positivas se acumulan en la parte superior de la tira y las negativas en la parte inferior. Un campo eléctrico E sub H apunta hacia abajo. La carga en movimiento experimenta una fuerza hacia arriba e E sub H y una fuerza hacia abajo e v sub d B. En la figura b, una carga positiva se mueve hacia la izquierda con velocidad v d. Las cargas negativas se acumulan en la parte superior de la tira, las cargas positivas en la parte inferior de la tira. Un campo eléctrico E sub H apunta hacia arriba. La carga en movimiento experimenta una fuerza hacia arriba e E sub H y una fuerza hacia abajo e v sub d B.
Un escenario en el que los campos eléctrico y magnético son perpendiculares entre sí se denomina situación de campo cruzado. Si estos campos producen fuerzas iguales y opuestas sobre una partícula cargada con la velocidad que iguala las fuerzas, estas partículas son capaces de pasar a través de un aparato, llamado selector de velocidad, sin desviarse. Esta velocidad se representa en la ecuación \ref{11.26}. Cualquier otra velocidad de una partícula cargada enviada a los mismos campos sería desviada por la fuerza magnética o la fuerza eléctrica.
Volviendo al efecto Hall, si la corriente en la tira es I, entonces a partir de Corriente y Resistencia, sabemos que
donde n es el número de portadores de carga por volumen y A es el área de la sección transversal de la tira. Combinando las ecuaciones para \(v_d\) e I resulta en
El campo E se relaciona con la diferencia de potencial V entre los bordes de la tira por
La cantidad \(V\) se llama potencial de Hall y se puede medir con un voltímetro. Finalmente, combinando las ecuaciones para I y E nos da
donde el borde superior de la tira en la Figura \(\PageIndex{1}\a) es positivo con respecto al borde inferior.
También podemos combinar la Ecuación \ref{11.24} y la Ecuación \ref{11.28} para obtener una expresión para el voltaje Hall en términos del campo magnético:
¿Qué pasa si los portadores de carga son positivos, como en la Figura \(\PageIndex{1}\)? Para la misma corriente I, la magnitud de V sigue dada por la ecuación \ref{hallV}. Sin embargo, el borde superior es ahora negativo con respecto al borde inferior. Por lo tanto, simplemente midiendo el signo de V, podemos determinar el signo de los portadores de carga mayoritarios en un metal.
Las medidas del potencial de Hall muestran que los electrones son los portadores de carga dominantes en la mayoría de los metales. Sin embargo, los potenciales de Hall indican que para unos pocos metales, como el tungsteno, el berilio y muchos semiconductores, la mayoría de los portadores de carga son positivos. Resulta que la conducción por carga positiva está causada por la migración de sitios de electrones perdidos (llamados huecos) en los iones. La conducción por huecos se estudia más adelante en Física de la Materia Condensada.
El efecto Hall puede utilizarse para medir campos magnéticos. Si un material con una densidad conocida de portadores de carga n se coloca en un campo magnético y se mide V, entonces el campo se puede determinar a partir de la ecuación \ref{11.29}. En los laboratorios de investigación en los que los campos de los electroimanes utilizados para mediciones precisas tienen que ser extremadamente estables, se suele utilizar una «sonda Hall» que forma parte de un circuito electrónico que regula el campo.
Ejemplo \(\PageIndex{1}\N-): Selector de velocidad
Un haz de electrones entra en un selector de velocidad de campo cruzado con campos magnéticos y eléctricos de 2,0 mT y \(6,0 \times 10^3 \, N/C\), respectivamente. (a) ¿Cuál debe ser la velocidad del haz de electrones para atravesar los campos cruzados sin desviarse? Si se desactiva el campo eléctrico, (b) ¿cuál es la aceleración del haz de electrones y (c) cuál es el radio del movimiento circular resultante?
Estrategia
El haz de electrones no se desvía por ninguno de los campos magnéticos o eléctricos si estas fuerzas están equilibradas. A partir de estas fuerzas equilibradas, calculamos la velocidad del haz. Sin el campo eléctrico, sólo se utiliza la fuerza magnética en la segunda ley de Newton para encontrar la aceleración. Por último, el radio de la trayectoria se basa en el movimiento circular resultante de la fuerza magnética.
Solución
- La velocidad del haz de electrones no perturbado con campos cruzados se calcula mediante la ecuación \ref{11.25}: \
- La aceleración se calcula a partir de la fuerza neta del campo magnético, igual a la masa por la aceleración. La magnitud de la aceleración es: \\N – El radio de la trayectoria proviene de un balance de las fuerzas circulares y magnéticas, o de la ecuación \N – 11.25: \
Significado
Si los electrones en el haz tuvieran velocidades por encima o por debajo de la respuesta en la parte (a), esos electrones tendrían una fuerza neta más fuerte ejercida por el campo magnético o eléctrico. Por lo tanto, sólo aquellos electrones con esta velocidad específica lo conseguirían.
La figura (\PageIndex{2}) muestra una cinta de plata cuya sección transversal es de 1,0 cm por 0,20 cm. La cinta lleva una corriente de 100 A de izquierda a derecha, y se encuentra en un campo magnético uniforme de magnitud 1,5 T. Utilizando un valor de densidad de \(n = 5,9 \times 10^{28}\ para la plata, encuentre el potencial Hall entre los bordes de la cinta.
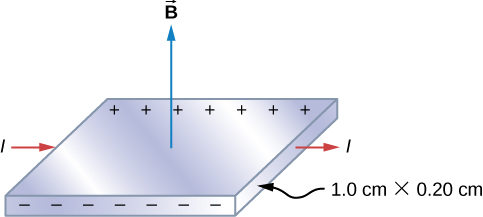
Estrategia
Como la mayoría de los portadores de carga son electrones, la polaridad de la tensión Hall es la indicada en la figura. El valor de la tensión Hall se calcula mediante la ecuación \ref{hallV}.
Solución
Al calcular la tensión Hall, necesitamos conocer la corriente que atraviesa el material, el campo magnético, la longitud, el número de portadores de carga y el área. Como todos estos datos están dados, la tensión Hall se calcula como:
&= \frac{(100 \, A)(1.5 \, T)(1,0 \times 10^{-2}m)}(5,9 \times 10^{28} /m^3)(1,6 \times 10^{-19}C)(2,0 \times 10^{-5}m^2)} &= 7,9 veces 10^{-6}V. Finalizar \N – [
Significado
Como en este ejemplo, el potencial Hall es generalmente muy pequeño, y se requiere una cuidadosa experimentación con equipos sensibles para su medición.
Ejercicio \(\PageIndex{1})
Una sonda Hall está formada por una tira de cobre, \(n = 8,5 \times 10^{28}\) electrones por metro cúbico, que tiene 2,0 cm de ancho y 0,10 cm de espesor. ¿Cuál es el campo magnético cuando I = 50 A y el potencial Hall es
- (4,0 \, \mu V\) y
- (6,0 \, \mu V\)?
Respuesta a
1,1 T
Respuesta b
1.6 T
Contribuidores y atribuciones
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), y Bill Moebs con muchos autores colaboradores. Esta obra está licenciada por OpenStax University Physics bajo una Licencia de Atribución de Creative Commons (por 4.0).