Una base vectorial de un espacio vectorial 
se define como un subconjunto 
de vectores en 
que son linealmente independientes y abarcan 
. En consecuencia, si 
es una lista de vectores en 
, entonces estos vectores forman una base vectorial si y sólo si cada 
puede escribirse unívocamente como
 |
(1)
|
donde 
son elementos del campo base.
Cuando el campo base son los reales de manera que 
para 
, los vectores base resultantes son 
-tuplas de reales que abarcan el espacio euclidiano 
-dimensional 
. Otros campos base posibles son los complejos 
, así como varios campos de característica positiva considerados en álgebra, teoría de números y geometría algebraica.
Un espacio vectorial 
tiene muchas bases vectoriales diferentes, pero siempre hay el mismo número de vectores base en cada una de ellas. El número de vectores base en 
se llama dimensión de 
. Cada lista de extensión en un espacio vectorial puede reducirse a una base del espacio vectorial.
El ejemplo más sencillo de una base vectorial es la base estándar en el espacio euclidiano 
, en la que los vectores base se encuentran a lo largo de cada eje de coordenadas. Un cambio de base se puede utilizar para transformar vectores (y operadores) en una base dada a otra.
Dado un hiperplano definido por
 |
(2)
|
a base se puede encontrar resolviendo para 
en términos de 
, y 
. Realizando este procedimiento,
 |
(3)
|
Así que
 |
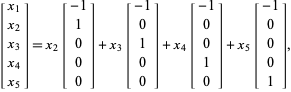(4)
|
y los vectores anteriores forman una base (no normalizada).
Dada una matriz 
con una base ortonormal, la matriz correspondiente a un cambio de base, expresada en términos de la original 
es
 |
(5)
|
Cuando un espacio vectorial es de dimensión infinita, entonces existe una base siempre que se asuma el axioma de elección. Un subconjunto de la base que es linealmente independiente y cuya extensión es densa se llama conjunto completo, y es similar a una base. Cuando 
es un espacio de Hilbert, un conjunto completo se llama base de Hilbert.