La función escalón de Heaviside es una función matemática denotada 
, o a veces 
o 
(Abramowitz y Stegun 1972, p. 1020), y también se conoce como «función escalonada unitaria». El término «función escalón de Heaviside» y su símbolo pueden representar una función constante a trozos o una función generalizada.
Cuando se define como una función constante a trozos, la función escalonada de Heaviside viene dada por
 |
(1)
|
(Abramowitz y Stegun 1972, p. 1020; Bracewell 2000, p. 61). El gráfico anterior muestra esta función (figura de la izquierda), y cómo aparecería si se visualizara en un osciloscopio (figura de la derecha).
Cuando se define como una función generalizada, puede definirse como una función 
tal que
 |
(2)
|
para 
la derivada de una función suficientemente suave 
que decae suficientemente rápido (Kanwal 1998).
The Wolfram Language representa la función generalizada de Heaviside como HeavisideTheta, mientras que utiliza UnitStep para representar la función piecewise Piecewise (que, cabe destacar, adopta la convención 
en lugar de la definición convencional 
).
La notación abreviada
 |
(3)
|
También se utiliza a veces.
La función escalón de Heaviside se relaciona con la función boxcar mediante
 |
(4)
|
y puede ser definirse en términos de la función de signo por
 |
(5)
|
La derivada de la función escalón viene dada por
 |
(6)
|
donde 
es la función delta (Bracewell 2000, p. 97).
La función escalón de Heaviside está relacionada con la función rampa 
por
 |
(7)
|
y a la derivada de 
por
 |
(8)
|
Los dos también están conectadas a través de
 |
(9)
|
donde 
denota convolución.
Bracewell (2000) da muchas identidades, algunas de las cuales son las siguientes. Dejando que 
denote la convolución,
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
 |
 |
 |
(13)
|
 |
 |
 |
(14)
|
Además,
 |
 |
 |
(15)
|
 |
 |
 |
(16)
|
La función escalonada de Heaviside puede definirse mediante los siguientes límites,
 |
 |
 |
(17)
|
 |
 |
 |
(18)
|
 |
 |
 |
(19)
|
 |
 |
 |
(20)
|
 |
 |
 |
(21)
|
 |
 |
 |
(22)
|
 |
 |
 |
(23)
|
 |
 |
 |
(24)
|
 |
 |
 |
(25)
|
 |
 |
 |
(26)
|
 |
 |
 |
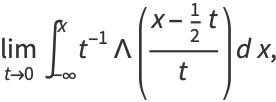(27)
|
donde 
es la función erfc, 
es la integral del seno, 
es la función sinc, y 
es la función triangular de un solo argumento. Las cuatro primeras se ilustran arriba para 
, 0,1 y 0,01.
Por supuesto, cualquier función monótona con asíntotas horizontales desiguales constantes es una función escalonada de Heaviside bajo una escala apropiada y una posible reflexión. La transformada de Fourier de la función escalón de Heaviside viene dada por
 |
 |
 |
(28)
|
 |
 |
 |
(29)
|
donde 
es la función delta.