Prueba de hipótesis e intervalo de confianzaEditar
El valor P de kappa rara vez se comunica, probablemente porque incluso los valores relativamente bajos de kappa pueden ser, sin embargo, significativamente diferentes de cero pero no de magnitud suficiente para satisfacer a los investigadores.:66Sin embargo, su error estándar ha sido descrito y es calculado por varios programas informáticos.
Los intervalos de confianza para Kappa pueden construirse, para los valores Kappa esperados si tuviéramos un número infinito de ítems comprobados, utilizando la siguiente fórmula:
C I : κ ± Z 1 – α / 2 S E κ {\displaystyle CI:\kappa \pm Z_{1-\alpha /2}SE_{\kappa }}

Donde Z 1 – α / 2 = 1.965 {{displaystyle Z_{1-\alpha /2}=1.965}


, y S E κ = p o ( 1 – p o ) N ( 1 – p e ) 2 {{displaystyle SE_{kappa }={sqrt {p_{o}(1-p_{o})} \sobre {N(1-p_{e})^{2}}}}}

Se calcula ignorando que pe se estima a partir de los datos, y tratando po como una probabilidad estimada de una distribución binomial mientras se utiliza la normalidad asintótica (es decir: suponiendo que el número de elementos es grande y que po no está cerca ni de 0 ni de 1). S E κ {\displaystyle SE_{\kappa }}

Interpretación de la magnitudEdit

Si la significación estadística no es una guía útil, ¿qué magnitud de kappa refleja un acuerdo adecuado? Las pautas serían útiles, pero otros factores distintos del acuerdo pueden influir en su magnitud, lo que hace que la interpretación de una magnitud determinada sea problemática. Como señalaron Sim y Wright, dos factores importantes son la prevalencia (los códigos son equiprobables o sus probabilidades varían) y el sesgo (las probabilidades marginales de los dos observadores son similares o diferentes). En igualdad de condiciones, los kappas son mayores cuando los códigos son equiprobables. En cambio, las kappas son mayores cuando los códigos se distribuyen de forma asimétrica por los dos observadores. En contraste con las variaciones de probabilidad, el efecto del sesgo es mayor cuando Kappa es pequeño que cuando es grande.:261-262
Otro factor es el número de códigos. A medida que aumenta el número de códigos, los kappas son mayores. Basándose en un estudio de simulación, Bakeman y sus colegas llegaron a la conclusión de que, para los observadores falibles, los valores de kappa eran más bajos cuando el número de códigos era menor. Y, de acuerdo con la afirmación de Sim & Wrights sobre la prevalencia, los kappas eran más altos cuando los códigos eran aproximadamente equiprobables. Así, Bakeman et al. concluyeron que «ningún valor de kappa puede considerarse universalmente aceptable»:357 También proporcionan un programa informático que permite a los usuarios calcular los valores de kappa especificando el número de códigos, su probabilidad y la precisión del observador. Por ejemplo, dados códigos equiprobables y observadores que tienen un 85% de precisión, el valor de kappa es de 0,49, 0,60, 0,66 y 0,69 cuando el número de códigos es de 2, 3, 5 y 10, respectivamente.
Sin embargo, en la literatura han aparecido pautas de magnitud. Quizás la primera fue la de Landis y Koch, que caracterizaron los valores < 0 como indicación de no acuerdo y 0-0,20 como leve, 0,21-0,40 como regular, 0,41-0,60 como moderado, 0,61-0,80 como sustancial y 0,81-1 como acuerdo casi perfecto. Sin embargo, este conjunto de directrices no es aceptado universalmente; Landis y Koch no aportan ninguna prueba que lo respalde, sino que lo basan en una opinión personal. Se ha señalado que estas directrices pueden ser más perjudiciales que útiles. Fleiss’s:218 igualmente arbitrario caracteriza los kappas por encima de 0,75 como excelente, de 0,40 a 0,75 como regular a bueno, y por debajo de 0,40 como pobre.
Kappa máximoEditar
Kappa asume su valor máximo teórico de 1 sólo cuando ambos observadores distribuyen los códigos de la misma manera, es decir, cuando las correspondientes sumas de filas y columnas son idénticas. Todo lo que sea menos es menos que un acuerdo perfecto. Aun así, el valor máximo que kappa podría alcanzar dadas distribuciones desiguales ayuda a interpretar el valor de kappa realmente obtenido. La ecuación para κ máximo es:
κ max = P max – P exp 1 – P exp {{displaystyle \kappa _{{max }={frac {P_{max }-P_{exp }}{1-P_{exp }}}}

donde P exp = ∑ i = 1 k P i + P + i {{displaystyle P_{\exp }={suma _{i=1}^{k}P_{i+}P_{+i}}

, como siempre, P max = ∑ i = 1 k min ( P i + , P + i ) {\displaystyle P_{\max }=\a suma _{i=1}^{k}min(P_{i+},P_{+i})}

,
k = número de códigos, P i + {{displaystyle P_{i+}}


son las probabilidades de columna.
LimitacionesEditar
Kappa es un índice que considera la concordancia observada con respecto a una concordancia de referencia. Sin embargo, los investigadores deben considerar cuidadosamente si el acuerdo de la línea de base de Kappa es relevante para la pregunta de investigación particular. La línea de base de Kappa se describe con frecuencia como el acuerdo debido al azar, lo cual es sólo parcialmente correcto. El acuerdo de la línea de base de Kappa es el acuerdo que se esperaría debido a la asignación aleatoria, dadas las cantidades especificadas por los totales marginales de la tabla de contingencia cuadrada. Por lo tanto, Kappa = 0 cuando la asignación observada es aparentemente aleatoria, independientemente del desacuerdo de la cantidad según los totales marginales. Sin embargo, para muchas aplicaciones, los investigadores deberían estar más interesados en el desacuerdo de la cantidad en los totales marginales que en el desacuerdo de la asignación como se describe por la información adicional en la diagonal de la tabla de contingencia cuadrada. Así, para muchas aplicaciones, la línea de base de Kappa distrae más que ilumina. Considere el siguiente ejemplo:
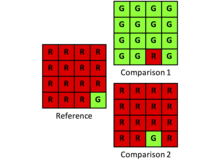
| Referencia | |||
|---|---|---|---|
| G | R | ||
| Comparación | G | 1 | 14 |
| R | 0 | 1 | |
La proporción de desacuerdo es de 14/16 o 0.875. El desacuerdo se debe a la cantidad porque la asignación es óptima. Kappa es de 0,01.
| Referencia | |||
|---|---|---|---|
| G | R | Comparación | G | 0 | 1 |
| R | 1 | 14 | |
La proporción de desacuerdo es de 2/16 o 0.125. El desacuerdo se debe a la asignación porque las cantidades son idénticas. Kappa es -0,07.
Aquí, informar del desacuerdo de cantidad y asignación es informativo mientras que Kappa oscurece la información. Además, Kappa introduce algunos retos en el cálculo y la interpretación porque Kappa es un ratio. Es posible que el ratio de Kappa devuelva un valor indefinido debido al cero en el denominador. Además, un ratio no revela su numerador ni su denominador. Es más informativo para los investigadores informar del desacuerdo en dos componentes, la cantidad y la asignación. Estos dos componentes describen la relación entre las categorías con más claridad que una sola estadística de resumen. Cuando el objetivo es la exactitud de la predicción, los investigadores pueden empezar a pensar más fácilmente en formas de mejorar una predicción utilizando dos componentes de cantidad y asignación, en lugar de una relación de Kappa.
Algunos investigadores han expresado su preocupación por la tendencia de κ a tomar las frecuencias de las categorías observadas como dadas, lo que puede hacer que no sea fiable para medir el acuerdo en situaciones como el diagnóstico de enfermedades raras. En estas situaciones, κ tiende a subestimar el acuerdo sobre la categoría rara. Por esta razón, κ se considera una medida de acuerdo demasiado conservadora. Otros refutan la afirmación de que kappa «tiene en cuenta» el acuerdo por azar. Para hacerlo de forma efectiva se necesitaría un modelo explícito de cómo el azar afecta a las decisiones de los evaluadores. El llamado ajuste de azar de las estadísticas kappa supone que, cuando no están completamente seguros, los calificadores simplemente adivinan, un escenario muy poco realista.