Tipos de matrices >
Una matriz 
es una matriz ortogonal si
 |
(1)
|
donde 
es la transposición de 
y 
es la matriz identidad. En particular, una matriz ortogonal es siempre invertible, y
 |
(2)
|
En forma de componente,
 |
(3)
|
Esta relación hace que las matrices ortogonales sean especialmente fáciles de calcular, ya que la operación de transposición es mucho más sencilla que el cálculo de una inversa.
Por ejemplo,
 |
 |
 |
(4)
|
 |
 |
 |
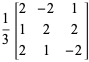(5)
|
son matrices ortogonales.
Una matriz 
se puede probar para ver si es ortogonal en Wolfram Language usando OrthogonalMatrixQ.
Las filas de una matriz ortogonal son una base ortonormal. Es decir, cada fila tiene longitud uno, y son mutuamente perpendiculares. Del mismo modo, las columnas también son una base ortonormal. De hecho, dada cualquier base ortonormal, la matriz cuyas filas son esa base es una matriz ortogonal. Automáticamente se da el caso de que las columnas son otra base ortonormal.
Las matrices ortogonales son precisamente aquellas matrices que preservan el producto interior
 |
(6)
|
Además, el determinante de 
es 1 o 
. Como subconjunto de 
, las matrices ortogonales no están conectadas ya que el determinante es una función continua. En su lugar, hay dos componentes correspondientes a si el determinante es 1 o 
. Las matrices ortogonales con 
son rotaciones, y tal matriz se llama matriz ortogonal especial.
El producto matricial de dos matrices ortogonales es otra matriz ortogonal. Además, la inversa de una matriz ortogonal es una matriz ortogonal, al igual que la matriz identidad. Por lo tanto, el conjunto de matrices ortogonales forman un grupo, llamado grupo ortogonal 
.