Definiciones estadísticas > Pruebas de bondad de ajuste
La prueba de bondad de ajuste se utiliza para probar si los datos de la muestra se ajustan a una distribución de una determinada población (es decir.es decir, una población con una distribución normal o una con una distribución Weibull). En otras palabras, le indica si los datos de su muestra representan los datos que esperaría encontrar en la población real. Las pruebas de bondad de ajuste utilizadas habitualmente en estadística son:
- La chi-cuadrado.
- Kolmogorov-Smirnov.
- Anderson-Darling.
- Shipiro-Wilk.
La prueba de bondad de ajuste chi-cuadrado
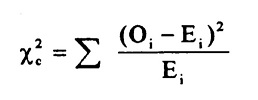
La fórmula chi-cuadrado.
La prueba de chi-cuadrado es la más común de las pruebas de bondad de ajuste y es la que encontrarás en estadística AP o en estadística elemental. La prueba de chi cuadrado se puede utilizar para distribuciones discretas como la distribución binomial y la distribución de Poisson, mientras que las pruebas de bondad de ajuste de Kolmogorov-Smirnov y Anderson-Darling sólo se pueden utilizar para distribuciones continuas.
Dos desventajas potenciales de la prueba de chi cuadrado son:
- La prueba de chi cuadrado sólo se puede utilizar para datos colocados en clases (bins). Si tiene datos no clasificados, tendrá que hacer una tabla de frecuencias o un histograma antes de realizar la prueba.
- Otra desventaja de la prueba de chi cuadrado es que requiere un tamaño de muestra suficiente para que la aproximación de chi cuadrado sea válida.
Hay otro tipo de prueba de chi cuadrado, llamada prueba de chi cuadrado para la independencia. A veces se confunden ambas, pero son muy diferentes.
- La prueba de chi-cuadrado para la independencia compara dos conjuntos de datos para ver si existe una relación.
- La bondad de ajuste de chi-cuadrado consiste en ajustar una variable categórica a una distribución.
Ambas pruebas utilizan el estadístico chi-cuadrado y la distribución. Para obtener más información sobre el cálculo del estadístico chi cuadrado, consulte:
El estadístico de la prueba chi cuadrado (incluye cálculos): ¿Qué es un estadístico chi cuadrado?
Ejecución de la prueba
Típicamente, esta prueba se ejecuta utilizando un software. La hipótesis nula para la prueba de bondad de ajuste chi-cuadrado es que los datos provienen de una distribución específica. La hipótesis alternativa es que los datos no provienen de una distribución específica.
Para interpretar la prueba, tendrá que elegir un nivel alfa (1%, 5% y 10% son comunes). La prueba chi-cuadrado devolverá un valor p. Si el valor p es pequeño (menor que el nivel de significación), puede rechazar la hipótesis nula de que los datos proceden de la distribución especificada.
Pruebas de bondad de ajuste menos comunes utilizadas en estadística elemental
Kolmogorov-Smirnov
Aunque se denomina prueba de normalidad, en realidad no le indica si una muestra concreta procede probablemente de una población normal. En cambio, le dirá cuando es poco probable que tenga una distribución normal. Una de las ventajas de esta prueba es que no hace ninguna suposición sobre la distribución de los datos. Una muestra puede compararse con una distribución utilizando una prueba K-S de una muestra o una prueba K-S de dos muestras. La prueba suele realizarse mediante un software (como el SPSS), ya que hay que calcular los valores críticos para cada distribución y encontrar las tablas de valores críticos no es una tarea fácil. La prueba suele recomendarse para muestras grandes de más de 2000. Para muestras más pequeñas, utilice Shapiro-Wilk.
Anderson-Darling
Esta prueba es una modificación de Kolmogorov-Smirnov. Es más sensible a las desviaciones en las colas de una distribución. Al igual que la de Kolmogorov-Smirnov, esta prueba le indicará cuándo es improbable que tenga una distribución normal y normalmente se ejecuta utilizando un software estadístico.
Shapiro-Wilk
Esta prueba calcula un valor W que le indicará si una muestra aleatoria procede de una población con distribución normal. La prueba se recomienda para muestras de hasta n=2000.
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Ratón, FL: CRC Press, pp. 536 y 571, 2002.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Vogt, W.P. (2005). Dictionary of Statistics & Metodología: Una guía no técnica para las ciencias sociales. SAGE.
Stephanie Glen. «Prueba de bondad de ajuste: ¿Qué es?» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/goodness-of-fit-test/
——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!