Introducción
El análisis de regresión se utiliza habitualmente para modelar la relación entre una única variable dependiente Y y uno o más predictores. Cuando tenemos un solo predictor, lo llamamos regresión lineal «simple»:
E = β0 + β1X
Es decir, el valor esperado de Y es una función rectilínea de X. Las betas se seleccionan eligiendo la línea que minimiza la distancia al cuadrado entre cada valor de Y y la línea de mejor ajuste. Las betas se eligen de forma que minimicen esta expresión:
∑i (yi – (β0 + β1X))2
Un instructivo gráfico que encontré en Internet

Fuente: http://www.unc.edu/~nielsen/soci709/m1/m1005.gif
Cuando tenemos más de un predictor, lo llamamos regresión lineal múltiple:
Y = β0 + β1X1+ β2X2+ β2X3+… + βkXk
Los valores ajustados (es decir, los valores predichos) se definen como aquellos valores de Y que se generan si introducimos nuestros valores de X en nuestro modelo ajustado.
Los residuos son los valores ajustados menos los valores reales observados de Y.
Aquí hay un ejemplo de regresión lineal con dos predictores y un resultado:
En lugar de la «línea de mejor ajuste», hay un «plano de mejor ajuste».
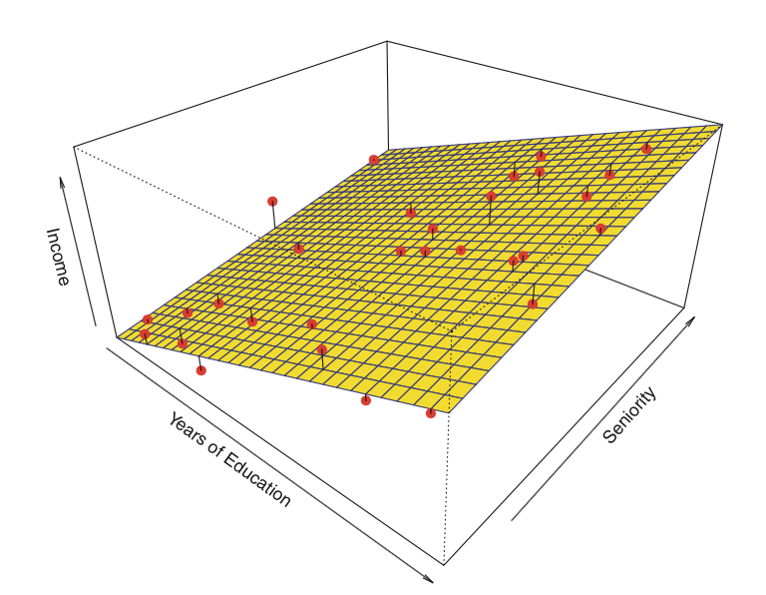
Fuente: James et al. Introduction to Statistical Learning (Springer 2013)
Hay cuatro supuestos asociados a un modelo de regresión lineal:
- Linealidad: La relación entre X y la media de Y es lineal.
- Homocedasticidad: La varianza del residuo es la misma para cualquier valor de X.
- Independencia: Las observaciones son independientes entre sí.
- Normalidad: Para cualquier valor fijo de X, Y se distribuye normalmente.
Revisaremos cómo evaluar estos supuestos más adelante en el módulo.
Comencemos con una regresión simple. En R, los modelos suelen ajustarse llamando a una función de ajuste de modelos, en nuestro caso lm(), con un objeto «fórmula» que describe el modelo y un objeto «data.frame» que contiene las variables utilizadas en la fórmula. Una llamada típica puede ser como
> mifunción <- lm(fórmula, datos, …)
y devolverá un objeto modelo ajustado, aquí almacenado como mifunción. Este modelo ajustado se puede imprimir, resumir o visualizar posteriormente; además, se pueden extraer los valores ajustados y los residuos, y podemos hacer predicciones sobre nuevos datos (valores de X) calculados mediante funciones como summary(), residuals(),predict(), etc. A continuación, veremos cómo ajustar una regresión lineal simple.
volver al principio | página anterior | página siguiente