Dopo aver letto questo capitolo, sarete in grado di fare quanto segue:
- Definire l’errore casuale e differenziarlo dal bias
- Illustrare l’errore casuale con esempi
- Interpretare un valore p-
- Interpretare un intervallo di confidenza
- Differenziare tra errori statistici di tipo 1 e di tipo 2 e spiegare come si applicano alla ricerca epidemiologica
- Descrivere come la potenza statistica influenza la ricerca
In questo capitolo, tratteremo l’errore casuale: da dove viene, come lo affrontiamo e cosa significa per l’epidemiologia.
Prima di tutto, l’errore casuale non è un bias. Il bias è un errore sistematico ed è trattato più in dettaglio nel capitolo 6.
L’errore casuale è proprio quello che sembra: errori casuali nei dati. Tutti i dati contengono errori casuali, perché nessun sistema di misurazione è perfetto. L’entità degli errori casuali dipende in parte dalla scala in cui qualcosa viene misurato (gli errori nelle misure a livello molecolare sarebbero dell’ordine dei nanometri, mentre gli errori nelle misure dell’altezza umana sono probabilmente dell’ordine di uno o due centimetri) e in parte dalla qualità degli strumenti utilizzati. I laboratori di fisica e di chimica hanno bilance molto accurate e costose che possono misurare la massa al grammo, microgrammo o nanogrammo più vicino, mentre la bilancia media nel bagno di qualcuno è probabilmente accurata entro una mezza libbra o libbra.
Per farvi capire l’errore casuale, immaginate di preparare una torta che richiede 6 cucchiai di burro. Per ottenere i 6 cucchiai di burro (tre quarti di un panetto, se ci sono 4 panetti in una libbra, come è vero di solito negli Stati Uniti), si potrebbero usare i segni che appaiono sulla carta cerata intorno al panetto, supponendo che siano allineati correttamente. Oppure potreste forse seguire il metodo di mia madre, che consiste nello scartare il bastone, fare un leggero segno a quello che sembra la metà del bastone, e poi arrivare ai tre quarti con un occhio alla metà della metà. Oppure si potrebbe usare il mio metodo, che è quello di prendere ad occhio il segno dei tre quarti dall’inizio e tagliare via. Ognuno di questi metodi di “misurazione” vi darà all’incirca 6 cucchiai di burro, che è certamente abbastanza buono per gli scopi della cottura di una torta, ma probabilmente non esattamente 3 once di valore, che è quanto pesano 6 cucchiai di burro negli Stati Uniti. La misura in cui sei leggermente sopra le 3 once questa volta e forse leggermente sotto le 3 once la prossima volta è causa di un errore casuale nella tua misurazione del burro. Se tu sottostimassi o sovrastimassi sempre, allora questo sarebbe un bias – tuttavia, le tue misurazioni costantemente sottostimate o sovrastimate conterrebbero di per sé un errore casuale.
Per qualsiasi variabile data che potremmo voler misurare in epidemiologia (ad es, altezza, GPA, frequenza cardiaca, numero di anni di lavoro in una particolare fabbrica, livello di trigliceridi nel siero, ecc.), ci aspettiamo che ci sia variabilità nel campione – cioè, non ci aspettiamo che tutti nella popolazione abbiano esattamente lo stesso valore. Questo non è un errore casuale. L’errore casuale (e la distorsione) si verifica quando cerchiamo di misurare queste cose. Infatti, l’epidemiologia come campo si basa su questa variabilità intrinseca. Se tutti fossero esattamente uguali, non saremmo in grado di identificare quali tipi di persone sono a più alto rischio di sviluppare una particolare malattia.
In epidemiologia, a volte le nostre misure si basano su un essere umano diverso dal partecipante allo studio che misura qualcosa sul o sul partecipante. Alcuni esempi sono l’altezza o il peso misurati, la pressione sanguigna o il colesterolo nel siero. Per alcuni di questi (ad esempio, il peso e il colesterolo sierico), l’errore casuale si insinua nei dati a causa dello strumento utilizzato – qui, una bilancia che ha probabilmente una fluttuazione di mezzo chilo, o un saggio di laboratorio con un margine di errore di pochi milligrammi per decilitro. Per altre misurazioni (ad esempio, altezza e pressione sanguigna), il misuratore stesso è responsabile di qualsiasi errore casuale, come nell’esempio del burro.
Tuttavia, molte delle nostre misurazioni si basano sull’auto-rapporto dei partecipanti. Ci sono interi libri di testo e classi dedicate alla progettazione dei questionari, e la scienza che sta dietro a come ottenere i dati più accurati dalle persone attraverso i metodi di indagine è abbastanza buona. Il Pew Research Center offre un bel tutorial introduttivo sulla progettazione del questionario sul suo sito web.
Rilevante per la nostra discussione qui, l’errore casuale apparirà anche nei dati del questionario. Per alcune variabili, ci saranno meno errori casuali di altre (ad esempio, l’autodichiarazione della razza è probabilmente abbastanza accurata), ma ce ne saranno comunque – ad esempio, persone che accidentalmente selezionano la casella sbagliata. Per altre variabili, ci saranno più errori casuali (ad esempio, risposte imprecise a domande come “Nell’ultimo anno, quante volte al mese ha mangiato riso?”). Una buona domanda da porsi quando si considera la quantità di errore casuale che potrebbe esserci in una variabile derivata da un questionario è: “Le persone possono dirmi questo?” La maggior parte delle persone potrebbe teoricamente dirvi quanto hanno dormito la scorsa notte, ma sarebbe difficile per loro dirvi quanto hanno dormito la stessa notte un anno fa. Il fatto che ve lo dicano o meno è una questione diversa e riguarda la distorsione (vedi capitolo 6). Indipendentemente da ciò, l’errore casuale nei dati dei questionari aumenta man mano che diminuisce la probabilità che le persone possano dirvi la risposta.
Quantificare l’errore casuale
Mentre possiamo – e dovremmo – lavorare per minimizzare l’errore casuale (usando strumenti di alta qualità, addestrando il personale su come prendere le misure, progettando buoni questionari, etc.), esso non può mai essere eliminato completamente. Fortunatamente, possiamo usare la statistica per quantificare gli errori casuali presenti in uno studio. Infatti, è a questo che serve la statistica. In questo libro, coprirò solo una piccola fetta del vasto campo della statistica: l’interpretazione dei valori p e degli intervalli di confidenza (CI). Piuttosto che concentrarmi su come calcolarli, mi concentrerò su cosa significano (e cosa non significano). La conoscenza dei valori p e degli IC è sufficiente per consentire un’interpretazione accurata dei risultati degli studi epidemiologici per gli studenti di epidemiologia principianti.
valori p
Quando si conduce una ricerca scientifica di qualsiasi tipo, compresa l’epidemiologia, si inizia con un’ipotesi, che viene poi testata man mano che lo studio viene condotto. Per esempio, se stiamo studiando l’altezza media degli studenti universitari, la nostra ipotesi (solitamente indicata da H1) potrebbe essere che gli studenti maschi sono, in media, più alti delle studentesse. Tuttavia, ai fini dei test statistici, dobbiamo riformulare la nostra ipotesi come ipotesi nulla. In questo caso, la nostra ipotesi nulla (di solito indicata con H0) sarebbe la seguente:
Abbiamo quindi intrapreso il nostro studio per verificare questa ipotesi. Per prima cosa determiniamo la popolazione di riferimento (studenti universitari) ed estraiamo un campione da questa popolazione. Misuriamo poi l’altezza e il sesso di tutti i membri del campione e calcoliamo l’altezza media degli uomini rispetto a quella delle donne. Condurremo poi un test statistico per confrontare le altezze medie nei 2 gruppi. Poiché abbiamo una variabile continua (l’altezza) misurata in 2 gruppi (uomini e donne), useremo un test t, e la statistica t calcolata tramite questo test avrà un valore p corrispondente, che è ciò che ci interessa veramente.
Diciamo che nel nostro studio troviamo che gli studenti maschi hanno un’altezza media di 5 piedi e 10 pollici, e tra le studentesse l’altezza media è 5 piedi e 6 pollici (per una differenza di 4 pollici), e calcoliamo un valore p di 0,04. Questo significa che se davvero non c’è differenza nell’altezza media tra studenti maschi e femmine (cioè, se l’ipotesi nulla è vera) e ripetiamo lo studio (fino a prelevare un nuovo campione dalla popolazione), c’è un 4% di possibilità che troveremo di nuovo una differenza nell’altezza media di 4 pollici o più.
Ci sono diverse implicazioni che derivano dal paragrafo precedente. In primo luogo, in epidemiologia calcoliamo sempre valori p-valori a 2 code. Qui questo significa semplicemente che il 4% di probabilità di una differenza di altezza ≥4 pollici non dice nulla su quale gruppo sia più alto – solo che un gruppo (sia maschi che femmine) sarà più alto in media di almeno 4 pollici. In secondo luogo, i valori p sono privi di significato se si è in grado di arruolare l’intera popolazione nel proprio studio. Per esempio, diciamo che la nostra domanda di ricerca riguarda gli studenti di Sanità Pubblica 425 (H425, Fondamenti di epidemiologia) durante il trimestre invernale 2020 alla Oregon State University (OSU). In questa popolazione sono più alti gli uomini o le donne? Poiché la popolazione è abbastanza piccola e tutti i membri sono facilmente identificabili, possiamo iscrivere tutti invece di dover fare affidamento su un campione. Ci sarà ancora un errore casuale nella misurazione dell’altezza, ma non useremo più un valore p per quantificarlo. Questo perché se dovessimo ripetere lo studio, troveremmo esattamente la stessa cosa, dato che abbiamo effettivamente misurato tutti nella popolazione. I valori P si applicano solo se stiamo lavorando con i campioni.
Infine, notate che il valore p descrive la probabilità dei vostri dati, assumendo che l’ipotesi nulla sia vera – non descrive la probabilità che l’ipotesi nulla sia vera dati i vostri dati. Questo è un errore di interpretazione comune fatto sia dai lettori principianti che da quelli più anziani di studi epidemiologici. Il valore p non dice nulla su quanto sia probabile che l’ipotesi nulla sia vera (e quindi, al contrario, sulla verità della vostra ipotesi reale). Piuttosto, quantifica la probabilità di ottenere i dati che avete ottenuto se l’ipotesi nulla fosse vera. Questa è una distinzione sottile ma molto importante.
Significatività statistica
Cosa succede dopo? Abbiamo un p-value, che ci dice la probabilità di ottenere i nostri dati data l’ipotesi nulla. Ma cosa significa effettivamente in termini di cosa concludere sui risultati di uno studio? Nella salute pubblica e nella ricerca clinica, la pratica standard è di usare p ≤ 0,05 per indicare la significatività statistica. In altre parole, decenni di ricercatori in questo campo hanno deciso collettivamente che se la probabilità di commettere un errore di tipo I (di cui parleremo più avanti) è del 5% o meno, “rifiuteremo l’ipotesi nulla”. Continuando l’esempio dell’altezza di cui sopra, concluderemo quindi che c’è una differenza di altezza tra i generi, almeno tra gli studenti universitari. Per valori di p superiore a 0,05, “non riusciamo a rifiutare l’ipotesi nulla” e concludiamo invece che i nostri dati non forniscono alcuna prova che ci sia una differenza di altezza tra gli studenti universitari maschi e femmine.
Se p > 0,05, non riusciamo a rifiutare l’ipotesi nulla. Non accettiamo mai l’ipotesi nulla perché è molto difficile dimostrare l’assenza di qualcosa. “Accettare” l’ipotesi nulla implica che abbiamo dimostrato che non c’è davvero alcuna differenza di altezza tra studenti maschi e femmine, il che non è successo. Se p > 0,05, significa semplicemente che non abbiamo trovato prove contrarie all’ipotesi nulla – non che tali prove non esistano. Potremmo aver ottenuto un campione strano, potremmo aver avuto un campione troppo piccolo, ecc. C’è un intero campo di ricerca clinica (comparative effectiveness researchvi) dedicato a dimostrare che un trattamento non è migliore o peggiore di un altro; i metodi del campo sono complessi, e le dimensioni del campione richieste sono piuttosto grandi. Per la maggior parte degli studi epidemiologici, ci limitiamo a rifiutare.
Il limite p ≤ 0,05 è arbitrario? Assolutamente sì. Vale la pena tenerlo a mente, in particolare per i valori di p molto vicini a questo limite. 0,49 è davvero così diverso da 0,51? Probabilmente no, ma sono ai lati opposti di quella linea arbitraria. La dimensione di un p-value dipende da 3 cose: la dimensione del campione, la dimensione dell’effetto (è più facile rifiutare l’ipotesi nulla se la vera differenza di altezza – se dovessimo misurare tutti nella popolazione, piuttosto che solo il nostro campione – è di 6 pollici piuttosto che 2 pollici), e la consistenza dei dati, più comunemente misurata dalle deviazioni standard intorno alle altezze medie nei 2 gruppi. Quindi un valore p di 0,51 potrebbe quasi certamente essere reso più piccolo semplicemente arruolando più persone nello studio (questo riguarda la potenza, che è l’inverso dell’errore di tipo II, discusso sotto). È importante tenere a mente questo fatto quando si leggono gli studi.
I test di significatività statistica fanno parte di una branca della statistica nota come statistica frequentista.ii Sebbene sia estremamente comune in epidemiologia e nei campi correlati, questa pratica non è generalmente considerata una scienza ideale, per una serie di motivi. In primo luogo, la soglia di 0,05 è del tutto arbitraria,iii e un test di significatività rigoroso rifiuterebbe il nullo per p = 0,049 ma non lo farebbe per p = 0,051, anche se sono quasi identici. In secondo luogo, ci sono molte più sfumature nell’interpretazione dei valori di p e degli intervalli di confidenza rispetto a quelle che ho trattato in questo capitolo.iv Per esempio, il valore di p sta realmente testando tutte le ipotesi di analisi, non solo l’ipotesi nulla, e un grande valore di p spesso indica semplicemente che i dati non possono discriminare tra numerose ipotesi concorrenti. Tuttavia, poiché la salute pubblica e la medicina clinica richiedono entrambe decisioni sì o no (dobbiamo spendere risorse per quella campagna di educazione sanitaria? Questo paziente dovrebbe prendere questo farmaco?), ci deve essere qualche sistema per decidere sì o no, e il test di significatività statistica è attualmente questo. Ci sono altri modi di quantificare l’errore casuale, e infatti la statistica bayesiana (che invece di una risposta sì o no fornisce una probabilità che qualcosa accada)ii sta diventando sempre più popolare. Tuttavia, poiché la statistica frequentista e il test dell’ipotesi nulla sono ancora di gran lunga i metodi più comunemente usati nella letteratura epidemiologica, essi sono l’obiettivo di questo capitolo.
Erori di tipo I e di tipo II
Un errore di tipo I (di solito simboleggiato da α, la lettera greca alfa, e strettamente legato ai valori p) è la probabilità che si rifiuti erroneamente l’ipotesi nulla – in altre parole, che si “trovi” qualcosa che in realtà non esiste. Scegliendo 0,05 come soglia di significatività statistica, noi nel campo della salute pubblica e della ricerca clinica abbiamo tacitamente concordato che siamo disposti ad accettare che il 5% delle nostre scoperte siano in realtà errori di tipo I, o falsi positivi.
Un errore di tipo II (di solito simboleggiato da β, la lettera greca beta) è l’opposto: β è la probabilità che non si riesca a rifiutare l’ipotesi nulla – in altre parole, che si perda qualcosa che in realtà esiste.
La potenza negli studi epidemiologici varia ampiamente: idealmente dovrebbe essere almeno del 90% (il che significa che il tasso di errore di tipo II è del 10%), ma spesso è molto più basso. La potenza è proporzionale alla dimensione del campione, ma in modo esponenziale – la potenza sale con l’aumentare della dimensione del campione, ma per passare dal 90 al 95% di potenza richiede un salto molto più grande nella dimensione del campione che per passare dal 40 al 45% di potenza. Se uno studio non riesce a rifiutare l’ipotesi nulla, ma i dati sembrano che ci potrebbe essere una grande differenza tra i gruppi, spesso il problema è che lo studio era sottopotenziato, e con un campione più grande, il p-value sarebbe probabilmente sceso sotto il magico 0,05 cutoff. D’altra parte, parte del problema con i piccoli campioni è che si potrebbe per caso aver ottenuto un campione non rappresentativo, e l’aggiunta di ulteriori partecipanti non porterebbe i risultati verso la significatività statistica. Come esempio, supponiamo di essere nuovamente interessati alle differenze di altezza basate sul genere, ma questa volta solo tra gli atleti universitari. Iniziamo con uno studio molto piccolo: solo una squadra maschile e una femminile. Se scegliamo, per esempio, la squadra maschile di pallacanestro e la squadra femminile di ginnastica, è probabile che troviamo una differenza enorme nelle altezze medie, forse 18 pollici o più. Aggiungendo altre squadre al nostro studio si otterrebbe quasi certamente una differenza molto più stretta nelle altezze medie, e la differenza di 18 pollici “trovata” nel nostro piccolo studio iniziale non reggerebbe nel tempo.
Intervalli di confidenza
Perché abbiamo fissato il livello \alfa accettabile al 5%, in epidemiologia e campi correlati, usiamo più comunemente intervalli di confidenza al 95% (95% CI). Si può usare un IC al 95% per fare test di significatività: se l’IC al 95% non include il valore nullo (0 per la differenza di rischio e 1,0 per odds ratio, risk ratio e rate ratio), allora p < 0.05, e il risultato è statisticamente significativo.
Anche se il 95% dei CI può essere usato per i test di significatività, essi contengono molte più informazioni del semplice fatto che il p-value sia < 0,05 o meno. La maggior parte degli studi epidemiologici riporta il 95% di CI intorno a qualsiasi stima puntuale che viene presentata. L’interpretazione corretta di un IC al 95% è la seguente:
Possiamo illustrare questo anche visivamente:
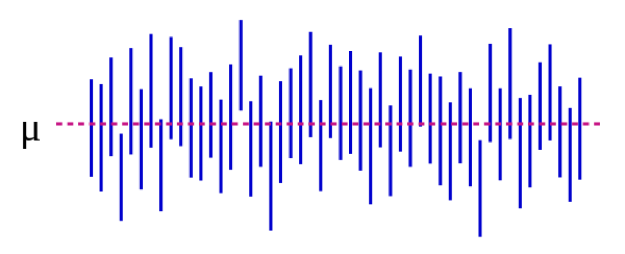
Fonte: https://es.wikipedia.org/wiki/Intervalo_de_confianza
Nella Figura 5-1, il parametro della popolazione μ rappresenta la risposta “reale” che si otterrebbe se si potesse iscrivere allo studio assolutamente tutti i membri della popolazione. Noi stimiamo μ con i dati del nostro campione. Continuando con il nostro esempio dell’altezza, questo potrebbe essere di 5 pollici: se potessimo magicamente misurare l’altezza di ogni singolo studente universitario negli Stati Uniti (o nel mondo, a seconda di come avete definito la vostra popolazione target), la differenza media tra studenti maschi e femmine sarebbe di 5 pollici. È importante notare che questo parametro della popolazione è quasi sempre inosservabile – diventa osservabile solo se si definisce la popolazione abbastanza stretta da poter iscrivere tutti. Ogni linea verticale blu rappresenta l’IC di un singolo “studio” – 50 di essi, in questo caso. Gli IC variano perché il campione è leggermente diverso ogni volta – tuttavia, la maggior parte degli IC (tutti tranne 3, in effetti) contengono μ.
Se conduciamo il nostro studio e troviamo una differenza media di 4 pollici (95% CI, 1,5 – 7), l’IC ci dice 2 cose. In primo luogo, il p-value per il nostro t-test sarebbe <0,05, poiché l’IC esclude lo 0 (il valore nullo in questo caso, poiché stiamo calcolando una misura di differenza). In secondo luogo, l’interpretazione dell’IC è: se ripetessimo il nostro studio (compreso il prelievo di un nuovo campione) 100 volte, allora 95 di quelle volte il nostro IC includerebbe il valore reale (che qui sappiamo essere 5 pollici, ma che nella vita reale non si può sapere). Quindi guardando l’IC qui di 1,5 – 7,0 pollici si ha un’idea di quale potrebbe essere la differenza reale – quasi certamente si trova da qualche parte all’interno di questo intervallo, ma potrebbe essere piccolo come 1,5 pollici o grande come 7 pollici. Come i valori p, gli IC dipendono dalla dimensione del campione. Un campione grande produrrà un CI relativamente più stretto. Gli IC più stretti sono considerati migliori perché danno una stima più precisa di quale potrebbe essere la risposta “vera”.
Sommario
L’errore casuale è presente in tutte le misurazioni, anche se alcune variabili sono più soggette di altre. I valori P e gli IC sono usati per quantificare l’errore casuale. Un valore p pari o inferiore a 0,05 è solitamente considerato “statisticamente significativo” e l’IC corrispondente esclude il valore nullo. Gli IC sono utili per esprimere la gamma potenziale del valore “reale” a livello di popolazione che viene stimato.
i. Burro negli Stati Uniti e nel resto del mondo. Errens Kitchen. Marzo 2014. https://www.errenskitchen.com/cooking-conversions/butter-measurement-weight-conversions/. Accesso al 26 settembre 2018. (↵ Return)
ii. Approccio bayesiano vs frequentista: stessi dati, risultati opposti. 365 Data Sci. agosto 2017. https://365datascience.com/bayesian-vs-frequentist-approach/. Accesso al 17 ottobre 2018. (↵ Ritorno 1) (↵ Ritorno 2)
iii. Smith RJ. Il continuo abuso dei test di significatività delle ipotesi nulle in antropologia biologica. Am J Phys Anthropol. 2018;166(1):236-245. doi:10.1002/ajpa.23399 (↵ Return)
iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. Valori P e salute riproduttiva: cosa possono imparare i ricercatori clinici dall’American Statistical Association? Hum Reprod Oxf Engl. 2016;31(11):2406-2410. doi:10.1093/humrep/dew192 (↵ Return)
v. Greenland S, Senn SJ, Rothman KJ, et al. Test statistici, valori p, intervalli di confidenza e potenza: una guida agli errori di interpretazione. Eur J Epidemiol. 2016;31:337-350. doi:10.1007/s10654-016-0149-3
vi. Perché è importante la ricerca sull’efficacia comparativa? Patient-Centered Outcomes Research Institute. https://www.pcori.org/files/why-comparative-effectiveness-research-important. Accesso al 17 ottobre 2018. (↵ Return)
- Non esiste una sola formula per calcolare un valore p o un CI. Piuttosto, le formule cambiano a seconda di quale test statistico viene applicato. Qualsiasi testo introduttivo di biostatistica che discute quali metodi statistici usare e quando dovrebbe fornire anche le informazioni corrispondenti sul calcolo del p-valore e dell’IC. ↵
- Non spendere troppo tempo a cercare di capire perché abbiamo bisogno di un’ipotesi nulla; lo facciamo e basta. La logica è sepolta in secoli di argomenti accademici di filosofia della scienza. ↵
- Come scegliere il test corretto va oltre lo scopo di questo libro – vedi qualsiasi libro di biostatistica introduttiva ↵
Interessante in tutte le misure. “Rumore” nei dati. Sarà sempre presente, ma la quantità dipende dalla precisione degli strumenti di misura. Per esempio, le bilance da bagno di solito hanno 0,5 – 1 libbra di errore casuale; i laboratori di fisica spesso contengono bilance che hanno solo pochi microgrammi di errore casuale (quelle sono più costose, e possono pesare solo piccole quantità). Si può ridurre la quantità in cui l’errore casuale influenza i risultati dello studio aumentando la dimensione del campione. Questo non elimina l’errore casuale, ma piuttosto permette al ricercatore di vedere meglio i dati all’interno del rumore. Corollario: l’aumento della dimensione del campione diminuirà il valore p e restringerà l’intervallo di confidenza, poiché questi sono modi di quantificare l’errore casuale.
Errore sistematico. L’errore di selezione deriva da un campionamento inadeguato (il vostro campione non è rappresentativo della popolazione di riferimento), da un basso tasso di risposta da parte di coloro che sono stati invitati a partecipare a uno studio, da un trattamento diverso di casi e controlli o di esposti/disesposti, e/o da una perdita disuguale al follow-up tra i gruppi. Per valutare il bias di selezione, chiedetevi “chi hanno preso, e chi hanno mancato?”–e poi chiedetevi anche “ha importanza”? A volte sì, altre volte, forse no.
Misclassificazione bias significa che qualcosa (l’esposizione, l’esito, un confonditore, o tutti e tre) sono stati misurati in modo improprio. Gli esempi includono persone che non sono in grado di dirvi qualcosa, persone che non sono disposte a dirvi qualcosa, e una misura oggettiva che è in qualche modo sistematicamente sbagliata (ad esempio sempre fuori nella stessa direzione, come un bracciale della pressione sanguigna che non è azzerato correttamente). Recall bias, social desirability bias, interviewer bias – questi sono tutti esempi di bias di misclassificazione. Il risultato finale di tutti loro è che le persone sono messe nella casella sbagliata in una tabella 2×2. Se l’errore di classificazione è equamente distribuito tra i gruppi (per esempio, sia gli esposti che i non esposti hanno la stessa probabilità di essere messi nella casella sbagliata), si tratta di errore di classificazione non differenziale. Altrimenti, si tratta di errore di classificazione differenziale.
Un modo di quantificare l’errore casuale. L’interpretazione corretta di un p-value è: la probabilità che, se si ripetesse lo studio (tornare alla popolazione target, estrarre un nuovo campione, misurare tutto, fare l’analisi), si troverebbe un risultato almeno altrettanto estremo, assumendo che l’ipotesi nulla sia vera. Se è effettivamente vero che non c’è differenza tra i gruppi, ma il tuo studio ha trovato che c’erano il 15% di fumatori in più nel gruppo A con un p-value di 0,06, allora significa che c’è un 6% di possibilità che, se tu ripetessi lo studio, troveresti di nuovo il 15% (o un numero maggiore) di fumatori in uno dei gruppi. Nella salute pubblica e nella ricerca clinica, di solito usiamo un cut-off di p < 0,05 per significare “statisticamente significativo” – quindi, stiamo permettendo un tasso di errore di tipo I del 5%. Così, il 5% delle volte “troveremo” qualcosa, anche se in realtà non c’è una differenza (cioè, anche se in realtà l’ipotesi nulla è vera). Il restante 95% delle volte, rifiutiamo correttamente l’ipotesi nulla e concludiamo che c’è una differenza tra i gruppi.
Un modo per quantificare l’errore casuale. L’interpretazione corretta di un intervallo di confidenza è: se ripetete lo studio 100 volte (tornate alla vostra popolazione target, prendete un nuovo campione, misurate tutto, fate l’analisi), allora 95 volte su 100 l’intervallo di confidenza che calcolate come parte di questo processo includerà il valore vero, assumendo che lo studio non contenga bias. Qui, il valore vero è quello che otterreste se foste in grado di arruolare tutti i membri della popolazione nel vostro studio – questo non è quasi mai effettivamente osservabile, poiché le popolazioni sono di solito troppo grandi per avere tutti inclusi in un campione. Corollario: Se la vostra popolazione è abbastanza piccola da poter avere tutti nel vostro studio, allora calcolare un intervallo di confidenza è irrilevante.
Usato nei test di significatività statistica. L’ipotesi nulla è sempre che non ci sia differenza tra i due gruppi in studio.
Un test statistico che determina se i valori medi in due gruppi sono diversi.
Un metodo in qualche modo arbitrario per determinare se credere o meno ai risultati di uno studio. Nella ricerca clinica ed epidemiologica, la significatività statistica è tipicamente fissata a p < 0,05, che significa un tasso di errore di tipo I del <5%. Come con tutti i metodi statistici, riguarda solo l’errore casuale; uno studio può essere statisticamente significativo ma non credibile, ad esempio, se c’è probabilità di bias sostanziale. Uno studio può anche essere statisticamente significativo (ad esempio, p era < 0,05) ma non clinicamente significativo (ad esempio, se la differenza nella pressione sanguigna sistolica tra i due gruppi era di 2 mm Hg – con un campione abbastanza grande questo sarebbe statisticamente significativo, ma non importa affatto clinicamente).
La probabilità che uno studio “trovi” qualcosa che non c’è. Tipicamente rappresentata da α, e strettamente legata ai valori p. Di solito fissato a 0,05 per studi clinici ed epidemiologici.
La probabilità che il vostro studio trovi qualcosa che c’è. Potenza = 1 – β; beta è il tasso di errore di tipo II. Studi piccoli, o studi di eventi rari, sono tipicamente sottopotenziati.
La probabilità che uno studio non trovi qualcosa che c’è. Tipicamente rappresentata da β, e strettamente correlata alla potenza. Idealmente sarà superiore al 90% per gli studi clinici ed epidemiologici, anche se in pratica questo spesso non accade.
La misura di associazione che viene calcolata in uno studio. Tipicamente presentata con un corrispondente intervallo di confidenza al 95%.