Frontiers | Rarefazione, Diversità Alfa e Statistica | Microbiologia

Introduzione

La metrica della diversità alfa riassume la struttura di una comunità ecologica rispetto alla sua ricchezza (numero di gruppi tassonomici), uniformità (distribuzione delle abbondanze dei gruppi), o entrambi. Poiché molte perturbazioni di una comunità influenzano la diversità alfa di una comunità, riassumere e confrontare la struttura della comunità attraverso la diversità alfa è un approccio onnipresente per analizzare le indagini comunitarie. In ecologia microbica, l’analisi della diversità alfa dei dati di sequenziamento di ampliconi è un primo approccio comune per valutare le differenze tra gli ambienti.

Purtroppo, determinare come stimare e confrontare in modo significativo la diversità alfa non è banale. Per illustrare, si consideri il seguente esempio in cui la metrica della diversità alfa di interesse è la ricchezza a livello di ceppo di una comunità microbica (il numero totale di varianti di ceppo presenti nell’ambiente). Supponiamo di condurre un esperimento in cui prendo un campione dall’ambiente A e conto il numero di diversi taxa microbici presenti nel mio campione. Poi prendo un campione dall’ambiente B, conto il numero di taxa diversi in quel campione e lo confronto con il numero di taxa nell’ambiente A. È probabile che osservi un numero maggiore di taxa diversi nel campione con più letture microbiche. Le dimensioni delle biblioteche possono dominare la biologia nel determinare il risultato dell’analisi della diversità (Lande, 1996).

La rarefazione è un metodo che regola le differenze nelle dimensioni delle biblioteche tra i campioni per facilitare il confronto della diversità alfa. Proposta per la prima volta da Sanders (1968), la rarefazione comporta la selezione di un numero specifico di campioni che è uguale o inferiore al numero di campioni nel campione più piccolo, e poi scartare casualmente le letture dai campioni più grandi fino a quando il numero di campioni rimanenti è uguale a questa soglia (vedi Hurlbert, 1971 per una versione deterministica). Sulla base di questi sottocampioni di uguali dimensioni, possono essere calcolate metriche di diversità che possono contrastare gli ecosistemi “equamente”, indipendentemente dalle differenze nelle dimensioni dei campioni (Weiss et al., 2017).

Purtroppo, la rarefazione non è giustificabile né necessaria, una visione inquadrata statisticamente da McMurdie e Holmes (2014) nel contesto del confronto delle abbondanze relative. In questo articolo, discuto perché le dimensioni disuguali del campione sembrano causare problemi speciali nell’analisi della diversità alfa. Introduco una prospettiva statistica sulla stima della diversità alfa, e sostengo che una visione comune degli indici di diversità sta causando problemi fondamentali nel confronto dei campioni. Senza sostenere alcun modello particolare di campionamento microbico, suggerisco un approccio generale per confrontare la diversità microbica, un approccio che tiene conto dell’incertezza nella stima degli indici di diversità. Tuttavia, poiché le stime per le metriche di diversità alfa sono fortemente distorte quando i taxa non sono osservati, il confronto della diversità alfa utilizzando dati grezzi o rarefatti non dovrebbe essere intrapreso. Descrivo la metodologia statistica per l’analisi della diversità alfa che aggiusta per i taxa mancanti, che dovrebbe essere usata al posto degli approcci comuni esistenti all’analisi della diversità in ecologia. Mentre il focus degli esempi è l’analisi dei dati del microbioma, i problemi e la discussione sono ugualmente applicabili all’analisi dei dati macroecologici. Inoltre, questa discussione si applica ugualmente alle analisi della diversità eseguite a livello di ceppo, specie o altri livelli tassonomici.

Errore di misurazione e varianza negli studi sul microbioma

Immaginate di avere una conoscenza completa di ogni microbo esistente, compresa l’identità, l’abbondanza e la posizione. Per confrontare la diversità microbica, potremmo definire ambienti specifici (ad esempio, l’intestino distale di donne di 35 anni che vivono negli Stati Uniti contigui) e confrontare le metriche di diversità attraverso diversi gradienti ecologici (ad esempio, con o senza diagnosi di sindrome dell’intestino irritabile). La diversità alfa potrebbe essere confrontata esattamente, perché conosceremmo intere popolazioni microbiche con perfetta precisione.

Purtroppo, non abbiamo la conoscenza di ogni microbo. Preleviamo campioni da ambienti e indaghiamo la comunità microbica presente nel campione. Usiamo i nostri risultati sul campione per trarre inferenze sull’ambiente che ci interessa veramente. I campioni non sono di particolare interesse, se non per il fatto che riflettono l’ambiente da cui sono stati prelevati. Man mano che campioniamo sempre di più l’ambiente utilizzando campioni più grandi, ci avviciniamo alla comprensione della vera e totale comunità microbica di interesse. Questo significa che man mano che aumentiamo il campionamento, il nostro calcolo di qualsiasi metrica di diversità si avvicina al valore di quella metrica di diversità calcolata utilizzando l’intera popolazione.

Osservare piccoli campioni da una grande popolazione non è un set-up sperimentale unico per l’ecologia microbica: è quasi universale in statistica. L’impostazione in cui una stima di una quantità converge al valore corretto man mano che si ottengono più campioni è anch’essa ben compresa in statistica. La proprietà unica degli esperimenti sul microbioma e dell’analisi della diversità alfa è che i campioni non rappresentano fedelmente l’intera comunità microbica in studio. C’è un errore non aggiustato nell’usare i nostri campioni come proxy dell’intera comunità.

Per illustrare questa distinzione, contrappongo gli esperimenti di diversità microbica a un esperimento non microbico. Supponiamo di essere interessati a modellare il flusso di CO2 del suolo trattato con diversi emendamenti. Misureremmo il flusso di siti di terreno di uguali dimensioni trattati con i diversi emendamenti, eseguendo repliche biologiche utilizzando più siti per ogni emendamento. Per valutare se gli emendamenti influenzano il flusso, adatteremo un modello di regressione (come l’ANOVA) al flusso con l’emendamento come variabile esplicativa. Implicitamente, questo modello riconosce che possiamo valutare il flusso con alta precisione; cioè, il margine di errore per determinare il flusso è trascurabile.

Ora supponiamo di sapere che la nostra macchina di misurazione del flusso sottostima costantemente il flusso esattamente di 5 unità. Ci regoleremmo per l’errore di misurazione aggiungendo 5 unità ad ogni misurazione prima di confrontarle. Ma cosa succede quando abbiamo un errore di misurazione casuale? Se l’errore di misurazione della macchina fosse casuale (per esempio, con 0 media e varianza di 1 unità per tutti gli emendamenti), questo non influenzerebbe nessun particolare emendamento. Tuttavia, rilevare una differenza tra gli effetti degli emendamenti sul flusso sarebbe statisticamente più impegnativo: avremmo bisogno di più campioni per rilevare una vera differenza rispetto al caso senza errore di misurazione. Per tenere conto del rumore sperimentale aggiuntivo, useremmo un modello che tenesse conto dell’errore di misurazione nella valutazione delle differenze tra gli emendamenti. Se la varianza dell’errore di misurazione fosse di 1 unità per l’emendamento A ma di 5 unità per l’emendamento B, ci regoleremmo allo stesso modo con un modello di errore di misurazione.

Per decidere se l’errore di misurazione deve essere tenuto in conto quando le osservazioni sono fatte in un esperimento, è necessario considerare l’effetto di ripetere il processo di osservazione sulla stessa unità sperimentale. Nell’esperimento di flusso, questo implicherebbe misurare nuovamente il flusso degli stessi siti del suolo usando le stesse condizioni sperimentali. Senza errori di misurazione nelle osservazioni, osserveremmo costantemente la stessa misura di flusso, mentre se avessimo un errore di misurazione casuale, molto probabilmente osserveremmo misure di flusso leggermente diverse. Poiché le repliche tecniche negli esperimenti sul microbioma producono diversi numeri di letture, diverse composizioni di comunità e diversi livelli di diversità alfa, abbiamo un errore di misurazione negli esperimenti microbici. Attualmente non teniamo conto dell’errore di misura negli studi sulla diversità microbica.

Bias nella stima e nel confronto della diversità alfa

Mentre l’errore di misura negli studi sul microbioma influisce su tutte le analisi dei dati del microbioma, la diversità alfa è particolarmente colpita perché le stime comunemente usate della diversità alfa sono fortemente distorte rispetto ad altri problemi di stima in ecologia microbica (come la stima delle abbondanze relative). Alcuni strumenti per affrontare i problemi con bias nella diversità alfa esistono nella letteratura statistica (Chao e Bunge, 2002; Willis e Bunge, 2015; Arbel et al., 2016; Willis e Martin, 2018). Tuttavia, ci sono due pratiche errate che circondano la diversità alfa che stanno impedendo l’adozione di metodologie statisticamente motivate. La prima pratica consiste nell’utilizzare stime distorte degli indici di diversità alfa. La seconda pratica è trattare le stime della diversità alfa come quantità osservate con precisione che non hanno errori di misura.

Per chiarire questa discussione, mi concentrerò sulla ricchezza tassonomica (il caso più semplice), e in seguito generalizzerò l’argomento ad altre metriche di diversità alfa. Consideriamo l’impostazione della figura 1A, dove stiamo studiando 2 ambienti diversi, e la ricchezza dell’ambiente A (chiamiamola CA) è superiore alla ricchezza dell’ambiente B (CB). Supponiamo di avere due replicati biologici di campioni da ciascun ambiente: nA1 e nA2 letture dall’ambiente A, nB1 e nB2 letture dall’ambiente B, e nA1 < nB1 < nA2 < nB2. Sia cij la ricchezza osservata dell’ambiente i sul replicato j. Come può comunemente accadere nella pratica, cA1 < cA2 < cB1 < cB2.

FIGURA 1

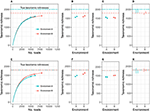
Figura 1. La ricchezza tassonomica attesa del campione aumenta con il numero di letture (A,E). Confrontare la ricchezza tassonomica dei campioni può quindi spesso portare a conclusioni errate sulla vera ricchezza (B,F). Anche la rarefazione dei campioni allo stesso numero di letture può portare a conclusioni errate (C,G). L’aggiustamento per i taxa non osservati e la contabilizzazione dell’incertezza nella stima rilevano correttamente sia le differenze vere (D) che quelle false (H) nella ricchezza. Mentre l’esempio qui impiegato riguarda la ricchezza microbica, lo stesso argomento si applica alla ricchezza macroecologica, così come ad altri indici di diversità alfa.

Attualmente ci sono due metodi comunemente usati per confrontare la diversità alfa. Il primo metodo, Figura 1B, consiste nell’utilizzare le stime cA1, cA2, cB1, e cB2, ed eseguire la modellazione e i test di ipotesi (come l’ANOVA) come se sia la distorsione che la varianza di queste stime fossero zero (vedi, per esempio, Makipaa et al., 2017). Nell’impostazione della Figura 1A, questo porta alla conclusione errata che l’ambiente A ha una ricchezza inferiore all’ambiente B. Il secondo metodo è quello di generare un campione normalizzato, o rarefatto, scartando casualmente le letture da tutti i campioni fino a quando ogni campione ha nA1 letture (il numero di letture nel campione più piccolo), Figura 1C. I livelli di ricchezza rarefatti risultanti sono quindi cA1, cA2′, cB1′ e cB2′. Queste stime sono poi utilizzati per la modellazione e test di ipotesi (vedi, per esempio, Arora et al., 2017). Questo porta alla conclusione che l’ambiente A e l’ambiente B non hanno ricchezze significativamente diverse, e le stime della ricchezza sono molto al di sotto delle ricchezze reali di ogni ecosistema (c’è un sostanziale bias negativo nelle stime), vietando il confronto della ricchezza tra diversi esperimenti. Inoltre, non tutte le informazioni raccolte dai campioni sono state utilizzate per fare il confronto.

Qui sostengo una terza strategia: aggiustare la ricchezza del campione di ogni ecosistema aggiungendovi una stima del numero di specie non osservate, stimare la varianza nella stima della ricchezza totale e confrontare le diversità rispetto a questi errori (Figura 1D). Questa opzione ha i vantaggi di sfruttare tutte le letture osservate, confrontando le stime del parametro effettivo di interesse (ricchezza tassonomica) e tenendo conto del rumore sperimentale. Nel caso in cui gli ambienti hanno una ricchezza uguale (Figure 1E-H), questo approccio rileva correttamente una ricchezza uguale, anche quando le strutture di abbondanza differiscono.

Modellare i parametri osservati con errore di stima non è un nuovo suggerimento: questo approccio viene dal campo della meta-analisi statistica, dove i risultati di più studi che stimano la stessa dimensione dell’effetto vengono confrontati (Demidenko, 2004; Willis et al., 2016; Washburne et al., 2018). Nelle meta-analisi, agli studi più grandi deve essere dato più peso nel determinare la dimensione dell’effetto complessivo, e questo è incorporato in una meta-analisi attraverso gli errori standard più piccoli sulle stime della dimensione dell’effetto. Allo stesso modo, quando si confronta la risposta di diversi gruppi di trattamento negli studi clinici, il numero di soggetti in ogni gruppo di trattamento viene preso in considerazione in un confronto dell’effetto complessivo del trattamento. L’aggiustamento per la dimensione del campione quando si confrontano diversi gruppi di osservazioni senza scartare i dati è ampiamente prevalente nelle scienze, e scartare i dati per aggiustare le dimensioni ineguali del campione è l’eccezione. La strategia qui delineata per la modellazione della ricchezza dopo l’aggiustamento per le specie mancanti aggiusta sia la distorsione che la varianza, rendendo così conto delle differenze nelle dimensioni della biblioteca e delle indagini microbiche incomplete.

Sebbene l’esempio discusso qui sia la ricchezza, questo approccio alla stima e al confronto della diversità alfa usando una correzione della distorsione (incorporando i taxa non osservati) e un aggiustamento della varianza (modello di errore di misurazione) potrebbe applicarsi a qualsiasi metrica della diversità alfa. Tuttavia, la stima della ricchezza ha una letteratura statistica ben studiata, e gli stimatori di ricchezza che sono adattati ai dati del microbioma esistono (vedi Bunge et al., 2014 per una revisione). Lo stesso non è vero per altre metriche di diversità alfa. Per esempio, gli stimatori Chao-Bunge (Chao e Bunge, 2002) e breakaway (Willis e Bunge, 2015) della ricchezza tassonomica forniscono stime della varianza, tengono conto dei taxa non osservati e non sono eccessivamente sensibili al conteggio dei singleton (il numero di specie osservate una volta). Al contrario, lo stimatore di entropia corretto per la copertura dell’indice di Shannon (Chao e Shen, 2003) fornisce stime della varianza e tiene conto dei taxa non osservati, ma è estremamente sensibile al conteggio dei singleton, che è spesso difficile da determinare negli studi sul microbioma. Mentre la stima della diversità alfa per i microbiomi è un’area attiva di ricerca in statistica (Arbel et al., 2016; Zhang e Grabchak, 2016; Willis e Martin, 2018), rimangono molte caratteristiche degli ecosistemi microbici (come il crosstalk tra i campioni e l’organizzazione spaziale dei microbi) che non sono ancora incorporate nella metodologia statistica per la stima della diversità alfa. Nonostante questo, le stime della diversità alfa che tengono conto dei taxa non osservati e forniscono stime della varianza sono ampiamente preferibili sia alle stime plug-in che a quelle rarefatte, che non tengono conto dei taxa non osservati né forniscono stime della varianza.

Discussione

Le stime plug-in di molti indici di diversità alfa (tra cui la ricchezza e la diversità di Shannon) sono negativamente distorte per il parametro della diversità alfa dell’ambiente, cioè, sottostimano la vera diversità alfa (Lande, 1996). Il tentativo di affrontare questo problema usando la rarefazione in realtà induce più bias. Questo è talvolta giustificato sostenendo che le stime rarefatte sono ugualmente distorte. Tuttavia, questo non è generalmente vero, perché gli ambienti possono essere identici per quanto riguarda una metrica di diversità alfa, ma le diverse strutture di abbondanza indurranno differenti distorsioni quando rarefatte. Per esempio, la Figura 1E mostra due ambienti con diverse strutture di abbondanza ma con uguale ricchezza; rarefacendo si ha la falsa impressione di una ricchezza disuguale (vedi anche Lande et al., 2000). In questo modo, sia la ricchezza del campione che la ricchezza rarefatta sono guidate da artefatti dell’esperimento (dimensione della libreria), e non puramente dalla struttura della comunità microbica. Al fine di trarre conclusioni significative sull’intera comunità microbica, è necessario aggiustare per il campionamento inesauribile utilizzando stime di parametri statisticamente motivate per la diversità alfa. Per trarre conclusioni significative riguardo ai confronti tra comunità microbiche, è necessario utilizzare modelli di errore di misurazione per correggere l’incertezza nella stima della diversità alfa.

Di recente è stato sostenuto che studiare la diversità microbica senza contesto ci sta distraendo dall’ottenere una comprensione dei meccanismi ecologici (Shade, 2016). A questa critica, aggiungo che l’errata applicazione degli strumenti statistici sta minando molte analisi della diversità alfa. Incoraggio gli ecologi microbici a usare stime della diversità alfa che tengano conto delle specie non osservate, e a usare la varianza delle stime nei modelli di errore di misura per confrontare la diversità tra gli ecosistemi.

Contributi dell’autore

AW ha scritto il manoscritto ed eseguito l’analisi dei dati.

Finanziamento

AW è sostenuto da fondi di avviamento assegnati dal Dipartimento di Biostatistica dell’Università di Washington, e dal National Institutes of Health (R35GM133420).

Conflitto di interessi

L’autore dichiara che la ricerca è stata condotta in assenza di relazioni commerciali o finanziarie che potrebbero essere interpretate come un potenziale conflitto di interessi.

Riconoscimenti

Questo articolo è basato sugli appunti presentati dall’autore al Marine Biological Laboratory al corso STAMPS nel 2013, 2014, 2015, 2016, 2017 e 2018. L’autore è grato a Berry Brosi, al MBL, ai direttori del corso STAMPS e ai partecipanti STAMPS per le innumerevoli discussioni su questo argomento. L’autore ringrazia anche Thea Whitman e due arbitri per molti suggerimenti ponderati sul manoscritto. Questo manoscritto è stato rilasciato come preprint via bioRxiv (Willis, 2017).

Arbel, J., Mengersen, K., e Rousseau, J. (2016). Modello bayesiano non parametrico dipendente per dati parzialmente replicati: l’influenza delle fuoriuscite di carburante sulla diversità delle specie. Ann. Appl. Stat. 10, 1496-1516. doi: 10.1214/16-AOAS944